Формула наращения по сложным процентам
Пусть первоначальная сумма долга равна P, тогда через один год сумма долга с присоединенными процентами составит P(1+i), через 2 года P(1+i)(1+i)=P(1+i)2, через n лет - P(1+i)n. Таким образом, получаем формулу наращения для сложных процентов
S=P(1+i)n, (19)
где S - наращенная сумма, i - годовая ставка сложных процентов, n - срок ссуды, (1+i)n - множитель наращения.
В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т.д.). Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен P, а знаменатель (1+i).
Отметим, что при сроке n<1 наращение по простым процентам дает больший результат, чем по сложным, а при n>1 - наоборот. В этом нетрудно убедиться на конкретных числовых примерах. Наибольшее превышение суммы, наращенной по простым процентам, над суммой, наращенной по сложным процентам, (при одинаковых процентных ставках) достигается в средней части периода.
Формула наращения по сложным процентам,
когда ставка меняется во времени
В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид
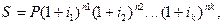 (20)
(20)
где i1, i2,..., ik - последовательные значения ставок процентов, действующих в периоды n1, n2,..., nk соответственно.