Основные понятия по теме

Для проверки гипотезы соответствия статистической функции распределения 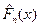теоретической функции F(x) (например, нормаль­ному закону) в практике обработки геофизических данных получили распро­странение критерии Колмогорова и Пир­сона (c²).

 

 

Согласно крите­рию Колмогорова вычисляется вели­чина

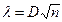, (3.1)

где 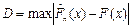– максимум модуля отклоне­ния статистической и теоретической функ­ций распределения. По величине l в со­ответствии с ее распределением находится вероятность P(l) совпадения распределений. Если P(l) мало (обычно <0,5), гипотеза о соответствии статистической и теоре­тической функции распределения отвергается.

Согласно критерию Пирсона вычисляется значение

(3.2)

где m_i – число значений случайной величины в i-ом разряде гистограммы; p_i – вероятности сравниваемого с экспериментальным теоретического распределения; r – число разрядов гистограммы.

По значению c² и числу степеней свободы k=r-s (s – число наложенных связей) с помощью таблицы вероятностей P(c²) определяют вероятность того, что величина, имеющая c² с k степенями свободы, превысит данное значение c². Если эта вероятность мала, гипотеза о соответствии экспериментального распределения теоретическому отвергается.

При сопоставлении статистической функции с нормальным законом распределения s=3, т.к. у распределения 2 параметра и одна связь забирается на задание конкретного вида распределения.

Теоретические частоты определяются следующим образом: находят оценки среднего и дисперси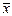и и 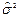. Полученные экспериментальные данные центрируют и нормируют, переходя к значениям 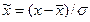, вычисляют концы разрядов гистограммы:

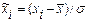. (3.3)

Далее вычисляют теоретические вероятности p_i попадания значений x в интервалы 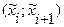по формуле

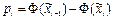
(пример 2).

Другая важная гипотеза – о принадлежности двух выборок к одной и той же генеральной совокупности (т.е. две выборки распределены по одному и тому же закону с одинаковыми параметрами).

Согласно критерию Смирнова-Колмогорова определяется величина

–

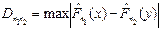максимальная разность двух функций распределения.

Далее вычисляется параметр

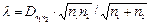(3.4)

и по таблице для распределения Колмогорова находится вероятность Р(l). Если Р(l) мало, гипотеза об одинаковом распределении двух выборок X и Y отвергается.

Используется также критерий c² в виде

 

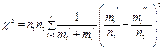, (3.5)

где 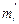и 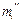- соответственно частоты сравниваемых выборок X и Y.

Этот критерий при больших n₁ и n₂ распределен по закону c² с (r-1) степенями свободы.

Часто вместо сравнения самих распределений, когда выборочное распределение построить трудно, ограничиваются проверкой гипотезы о равенстве числовых характеристик: среднего, дисперсии и других моментов распределения.

Для сравнения средних двух выборок X и Y можно использовать расчет доверительных интервалов:

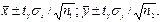(3.6)

Если эти интервалы пересекаются, то с вероятностью g можно утверждать равенство средних 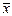и .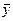

Более точный метод сравнения средних двух выборок базируется на критерии Стьюдента. Если распределения выборок принимаются нормальными, то равенство 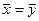с вероятностью g удовлетворяется при выполнении условия

t<t_g,

где

, (3.7)

а t_g - g- квантиль распределения Стьюдента с k= (n₁ + n₂ -2) степенями свободы.

Метод сравнения дисперсий в предположении о нормальности распределения обеих выборок основан на критерии Фишера. Вычисляется величина

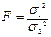, (3.8)

где s₁² и s₂² – выборочные дисперсии, причем s₁²>s₂².

Величина F подчиняется распределению Фишера с (n₁-1) и (n₂-1) степенями свободы.

Гипотеза о равенстве дисперсий принимается с вероятностью g при F<F_g, где F_g - g-квантиль распределения Фишера с (n₁-1) и (n₂-1) степенями свободы.

 

Пример 2 По данным примера 1 проверить нормальность распределения данных измерения плотности образца по критериям Пирсона (c²) и Колмогорова.

Для проверки гипотезы о нормальности распределения по критерию c² необходимо вычислить теоретические частоты. С этой целью определяют границы полученных интервалов (см. пример 1) для центрированной и нормированной случайной величины по формуле (3.3). Результат представлен в таблице 5 (графы 4 и 5).

Далее определяем вероятности попадания случайной величины в эти нормированные интервалы. Для этого, пользуясь таблицами нормального распределения, определяем значения центрированной и нормированной случайной величины на границах интервалов (столбцы 6,7 таблицы 5). Теоретические частоты np_i определяем по формуле

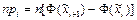(3.9)

(графа 8 таблицы 5).

Суммируя значения в столбце 9, определяем значение критерия c²=5,92. Оно меньше табличного значения c², полученного при 50%-ном уровне значимости с k=7 степенями свободы. Таким образом, гипотеза о нормальности полученного распределения не противоречит по критерию Пирсона результатам измерений.

 

Таблица 5 – Результаты статистической обработки данных

 

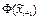
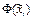
Разряд	Частота в интервале	Накопл. частоты	Нормиров. и центриров. интервалы			npi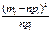
			- ∞	-1,77	0,0384		3,84	0,35
			-1,77	-1,36	0,0869	0,0384	4,85	2,06
			-1,36	-0,94	0,1736	0,0869	8,67	0,32
			-0,94	-0,52	0,3015	0,1736	12,79	1,32
			-0,52	-0,1	0,4602	0,3015	15,87	0,94
			-0,1	0,31	0,6217	0,4602	16,15	0,29
			0,31	0,73	0,7673	0,6217	14,56	0,17
			0,73	1,15	0,8749	0,7673	10,76	0,01
			1,15	1,56	0,9406	0,8749	6,57	0,31
			1,56	∞		0,9406	5,94	0,15

 

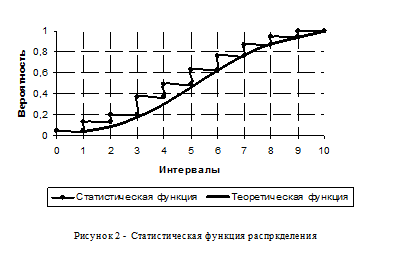
Согласно критерию Колмогорова, вычисляем величину

,

где .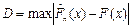

Сравнивая значения столбцов 3 и 6 таблицы 5, получаем максимальное расхождение между экспериментальной и теоретической функциями распределения D= 0,0685.

Таким образом, l=0,685, и по таблице распределения Колмогорова определяем Р(l)=0,84. Окончательно, согласно критериям Пирсона и Колмогорова гипотеза о нормальности распределения результатов измерения плотности горной породы принимается.

 

Вопросы для самоконтроля

 

1 Как проверяется гипотеза о соответствии статистической функции теоретической по критерию Колмогорова?

2 Как проверяется гипотеза о соответствии статистической функции теоретической по критерию Пирсона?

3 Как проверяется гипотеза о равенстве статистических распределений?

4 Как проверяется гипотеза о равенстве средних?

5 Как проверяется гипотеза о равенстве дисперсий? С какой целью проверяется эта гипотеза?