Решение

Вначале определим реакции опор А и Н. Для этого изобразим ферму, отбросим связи в точках А и Н и заменим их соответствующими силами реакции (рисунок 18).

Рисунок 18 – Расчетная схема

 

Составим три уравнения равновесия:

SFx=0, XH=0;	(22)
SFy=0, RA–Q–F+YH=0;	(23)
SMA=0, –Q·AC–F AE+YH·AH=0.	(24)

Решая совместно систему уравнений, получим Y_H = 50 кН, R_A = 40 кН.

1. Находим усилие в стержне № 1. Для этого рассечем ферму сечением I-I (рисунок 18) и рассмотрим равновесие левой части фермы. Действие отброшенной правой части фермы заменяем силами S₁, S₅, S₆, направляя их вдоль рассеченных стержней так, как будто стержни растянуты (рисунок 19).

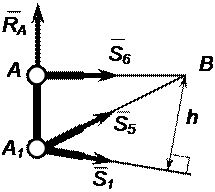
Рисунок 19 – Расчетная схема

Составим для левой части уравнение моментов относительно точки В:

SMB=0, –RA·AB+S1·h=0;	(25)
S1=RA·AB/h.

Для определения h рассмотрим рисунок 20.

 

 

Рисунок 15 – Геометрическая схема

 

Из подобия треугольников АА₁L и DD₁L имеем АL= 6а. Тогда

tg(a)=АА₁/АL=a/6a=1/6;

a=arctg(1/6) » 9,46°.

Величина h = BB₂ = BL·sin(a) = 8a·0,164 = 1,32a. И тогда

S₁ = R_A·AB/h = 40·2a/1,32a = 60,8(кН).

Стержень № 1 растягивается силой 60,8 кН.

2. Найдем усилие в раскосе № 2: рассечем ферму сечением II-II (рису- нок 18) и рассмотрим равновесие левой части фермы, нагруженной силами R_A, Q и усилиями S₂, S₇, и S₈ (рисунок 21).

Рисунок 21 – Расчетная схема

Составим для этой части фермы уравнение моментов всех сил относительно точки L.

SML=0, RA·LA–Q·LC+S2·LL1=0;	(26)
S2= (Q·LC–RA·LA)/LL1=(Q·10a–RA·6a)/d.

Для определения величины S₂ необходимо сначала определить d. Видно (рисунок 21) из треугольника LDL₁, что d = LD·sin(b). Угол b определим из треугольника CDC₁: tg(b)=CC₁/CD = / = 0,833; b = arctg(0,833) = 39,8°

Тогда d = LD•sin(b) = 12a•sin(39,8°) = 7,68a.

а величина S₂=(Q•10•a–R_A•6a)/7,68a = (30•10•a–40•6a)/7,68a =7,81 кН.

Стержень № 2 растянут усилием 7,81 кН

Определим также усилие S₈, необходимое для нахождения усилия в стержне № 3(рисунок 18). Составим для этой же части фермы (рисунок 21) уравнение

SFy=0, RA–Q+S2·sin(b)–S8·sin(a)=0.

(27)

Отсюда находим

S₈=(R_A–Q+S₂•sin(b))/sin(a)=(40–30+7,81•sin(39,8 °))/sin(9,46°)= 91,5 кН.

3. Для определения усилия S₃ в стержне № 3 рассмотрим равновесие узла D₁. Для этого вырежем узел D₁, заменив стержни усилиями (рисунок 22).

Рисунок 22 – Расчетная схема

Получим систему трех сходящихся сил: S₃, S₈ и S₉, две из которых, S₃ и S₉, неизвестны. Запишем систему уравнений

SFx=0, S9·cos(a)–S8·cos(a)=0;	(28)
SFy=0, S3+S8·sin(a)+S9·sin(a)=0;	(29)

Из первого уравнения S₉ = S₈ = 91,5 кН,

из второго уравнения S₃ = (S₈+S₉)•sin(a) = (91,5+91,5)•sin(9,46°) = –30 кН. Стержень № 3 сжат усилием 30 кН.

4. Найдем усилие в стержне № 4. Рассечем ферму сечением III-III (рису-нок 18) и рассмотрим равновесие правой части фермы: изобразим ее со всеми действующими на нее силами (рисунок 23).

Рисунок 23 – Расчетная схема

 

Силу Х_H не изображаем, т. к. получили ранее Х_H = 0;

Для этой части напишем уравнение моментов всех сил относительно точки E₁

SME1=0, YH·EH+S4·EE1=0;	(30)
S4 = –Y·EH/EE1 = –50·4a/1,66a = –120 кН.

Стержень № 4 сжат усилием 120 кН.

 

СПИСОК ЛИТЕРАТУРЫ

 

1 Методические указания к выполнению расчетно-графических заданий по разделу «Статика» курса «Теоретическая механика» / Р. К. Сиражетдинов [и др.]. – Курган.: Изд-во КГСХА, 1997. – 38 с.

2 Сборник задач для курсовых работ по теоретической механике /под ред. А.А.Яблонского. – М.: Высшая школа, 1985. – 367 с.

3 Турбин, Б. И. Сборник задач по теоретической механике /Б.И. Турбин, С.И. Рустамов. – Киев.: Высшая школа, 1978. – 160 с.

СОДЕРЖАНИЕ

 

Введение………………………………………………………………………………
Задача 1. Пространственная система сходящихся сил…………………….............
Задача 2. Жесткая рама под действием плоской системы сил…………………….
Задача 3. Система тел под действием плоской системы сил………………………
Задача 4. Равновесие тела под действием пространственной системы сил…………………………………………………………………
Задача 5. Равновесие фермы…………………………………………………………
Список литературы……….…………………………………………………………..