Решение
1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня DЕ (рисунок 10б). Изобразим действующие на стержень силы: силу F, реакцию N, направленную перпендикулярно стержню, и составляющие ХD и YD реакции шарнира D. Для полученной плоской системы сил составляем три уравнения равновесия:
| SFK x=0, XD +F – N · sin(60°)=0; | (10) |
| SFK y=0, YD +N · cos(60°)=0; | (11) |
| SMD (FK )=0, N · 2a – F · sin(60°)·5a=0. | (12) |
Решим систему уравнений в MathCAD (рисунок 11).
Рисунок 11 – Решение системы уравнений с неизвестными ХD, YD, N в MathCAD
2. Теперь рассмотрим равновесие угольника (рисунок 10в). На него действуют: сила давления стержня N¢, направленная противоположно реакции N; равномерно распределенная нагрузка, которую заменяем силой Q, приложенной в середине участка КВ (численно Q = q · 4а = 16 кН); пара сил с моментом М и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими ХА, YA , и пары с моментом МA. Для этой плоской системы сил тоже составляем три уравнения равновесия:
| SFKx=0, ХА+Q·cos(60°)+N' ·sin(60°)=0; | (13) |
| SFKy=0, YA – Q·sin(60°) – N' ·cos(60°)=0; | (14) |
| SМА=0, MA +M + Q·2·a + N' ·cos(60°)·4·a + N' ·cos(30°)·6·a =0. | (15) |
При вычислении момента силы N' разлагаем ее на составляющие N'1 и N'2 и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (13) – (15), найдем искомые реакции. При решении учитываем, что численно N' = N в силу равенства действия и противодействия.
Решим систему уравнений в MathCAD (рисунок 12).
Рисунок 12 – Решение системы уравнений
с неизвестными ХA, YA, MA в MathCAD
Ответ:N = 21,7 кН, YD = –10,8 кН, XD = 8,8 кН, XA = –26,8 кН,
YA = 24,7 кН, MA = –42,6 кНм. Знаки указывают, что силы YD, XА и момент МA имеют направления, противоположные показанным на рисунке.
ЗАДАЧА 4. РАВНОВЕСИЕ ТЕЛА ПОД ДЕЙСТВИЕМ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ
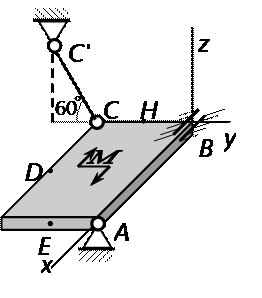
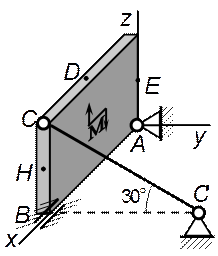
Однородная прямоугольная плита весом Р = 5 кН со сторонами АВ =3ℓ, ВС = 2ℓ закреплена в точке А сферическим шарниром, а в точке В - цилиндри-ческим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СС ' (рисунок 13).
Вариант 1
| 
Вариант 2
| ||
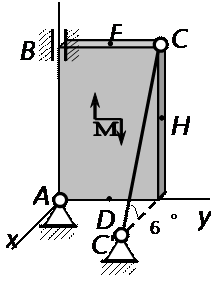Вариант 3
|
Вар |
Вариант 4
Рисунок 13 – Варианты эскизов
Продолжение рисунка 13
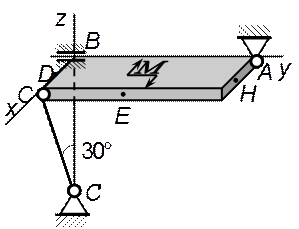
Вариант 5
| 
Вариант 6
|
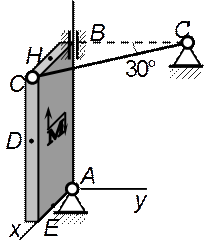Вариант 7
| 
Вариант 8
|
Вариант 9
| 
Вариант 10
|
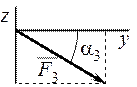
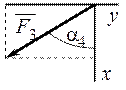
На плиту действуют пара сил с моментом М = 6 кН·м, лежащая в плоскости плиты, и две силы. Значения этих сил, их направления и точки приложения указаны в таблице 4; при этом силы F1 и F4 лежат в плоскостях, параллельных плоскости ху, сила F2 – в плоскости, параллельной xz, сила F3 – в плоскости, параллельной yz. Точки D, E, H находятся в серединах сторон плиты. Определить реакции связей в точках А, В и С. При окончательных подсчётах принять ℓ= 0,8 м.
Таблица 4 – Варианты расположения сил и точек их приложения
| Сила |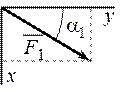 
| 
| 
| 
| ||||
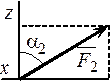
| F1 = 4 H | F2 = 6 H | F3 = 8 H | F4 = 10 H | |||||
| № условия | точка приложения | a1,° | точка приложения | a2,° | точка приложения | a3,° | точка приложения | a4, ° |
| D | – | – | E | – | – | |||
| H | D | – | – | – | – | |||
| – | – | E | – | – | D | |||
| – | – | – | – | E | H | |||
| E | – | – | H | – | – | |||
| – | – | D | H | – | – | |||
| – | – | H | – | – | D | |||
| E | H | – | – | – | – | |||
| – | – | – | – | D | E | |||
| – | – | E | D | – | – |
Указания. При решении задачи учесть, что реакция сферического шарнира (или подпятника) имеет три составляющие, а реакция цилиндрического шарнира – две составляющие, лежащие в плоскости, перпендикулярной оси шарнира. При вычислении моментов силы F удобно разложить ее на составляющие F ¢ и F ¢¢, параллельные координатным осям, тогда по теореме Вариньона, для оси х, например, Mx (F) = Mx (F ′) + Mx (F ′′).
Пример
Условие задачи. Вертикальная прямоугольная плита весом Р (рисунок 14) закреплена сферическим шарниром в точке А, цилиндрическим шарниром в точке В и невесомым стержнем DD¢ , лежащим в плоскости, параллельной плоскости yz. На плиту действуют сила F1 (в плоскости xz), сила F2 (параллельная оси y) и пара сил с моментом М (в плоскости плиты).
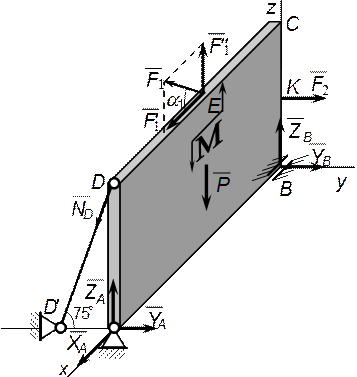
Рисунок 14 – Расчетная схема
Дано: P = 5 кН, M = 3 кН·м, F1 = 6 кН, F2 = 7,5 кН, a1 = 30°, АВ = 1 м,
ВС = 2 м, СЕ = 0,5·ВС, ВК = 0,5·ВС, q = 20 кН/м, a = 0,2 м.
Определить реакции в точках А, В и стержня DD '.