Воспроизводимости стандартного метода измерений (часть II)
СРАВНИТЕЛЬНЫЕ ИСПЫТАНИЯ ПРИ АККРЕДИТАЦИИ ИСПЫТАТЕЛЬНЫХ ЛАБОРАТОРИЙ
Методические указания к практическим работам
По дисциплине «Специальные системы сертификации»
Омск
Издательство ОмГТУ
Составитель:
Шендалева Елена Владимировна, канд. техн. наук
Методические указания направлены на получение практических навыков проведения межлабораторных сравнительных испытаний с использованием методов статистической обработки данных, описанных в стандартах ГОСТ Р ИСО 5725.
Методические указания предназначены для студентов специальности 200503 «Стандартизация и сертификация», изучающих дисциплину «Специальные системы сертификации».
Печатается по решению редакционно-издательского совета Омского государственного технического университета.
Практическая работа № 1
Основной метод определения повторяемости и
воспроизводимости стандартного метода измерений (часть II)
Цель работы
Изучение методов определения повторяемости и воспроизводимости в случае проведения сбалансированного эксперимента с однородными уровнями [1].
Описание
Пробы из j (j = 1, 2, ..., q) партий материалов, представляющих q различных уровней измеряемой характеристики, посылают в i (i = 1, 2, ... , p) лабораторий, каждая из которых в условиях повторяемости на каждом из q уровней получает k (k = 1, 2, ... , n) параллельных измерений. Такой эксперимент носит название сбалансированного эксперимента с однородными уровнями.
Каждую группу из n измерений, относящихся к одному уровню, выполняют в условиях повторяемости, т.е. в пределах короткого интервала времени, одним и тем же оператором, без перекалибровки аппаратуры. Любое изменение условий эксперимента регистрируют вместе с результатами.
Каждое сочетание лаборатории и уровня (определенного образца) носит название базового элемента эксперимента по оценке прецизионности. В идеальном случае результаты эксперимента с p лабораториями и q уровнями представляют собой таблицу с pq базовыми элементами, каждый из которых содержит n результатов измерений. Вследствие избыточных данных, недостающих данных и выбросов данная ситуация не всегда достигается на практике.
Иногда лаборатория может осуществить и запротоколировать более чем n официально заданных результатов измерений. Если они равнозначны, то должен быть произведен их случайный отбор с целью выбора запланированного количества результатов измерений.
Если некоторые из результатов измерений отсутствуют, то незаполненными базовыми элементами можно просто пренебречь, в то время как остальные базовые элементы учитывают в стандартной процедуре расчета.
Выбросы – это данные результатов измерений, которые настолько отклоняются от сопоставимых данных, что их признают несовместимыми. В случае наличия выбросов базовыми элементами можно пренебречь.
Когда на различных уровнях в одной и той же лаборатории получено несколько необъяснимых аномальных результатов измерений, данная лаборатория может рассматриваться как выброс, имеющий слишком высокую внутрилабораторную дисперсию и/или слишком большую внутрилабораторную систематическую погрешность. В таком случае целесообразно исключить некоторые или все данные такой выпадающей лаборатории.
Явно ошибочные данные должны быть исправлены или исключены.
Задание
1. На основе исходных данных построить формы Б и В [1].
2. Выполнить проверку на два выброса в результатах измерений.
3. Определить межлабораторные дисперсии, дисперсии повторяемости и воспроизводимости для каждого уровня измерений.
4. Установить функциональную зависимость между значениями прецизионности и средним значеним для уровня измерения.
5. Рассмотреть поэтапную процедуру статистического анализа.
Исходные данные
Исходные данные (табл. 1.1.) по параллельным измерениям на нескольких уровнях (4 лаборатории, 5 уровней измерения, 5 измерений на каждом уровне) представлены в форме А [2]:
Таблица 1.1
Исходные данные параллельных измерений
| Форма А – Рекомендуемая форма для сопоставления исходных данных | |||||||||||||||||||||||||
| Лаборатория p (i) | Уровень q (j) | ||||||||||||||||||||||||
| Измерения n (k) | Измерения n (k) | Измерения n (k) | Измерения n (k) | Измерения n (k) | |||||||||||||||||||||
| 9,750 | 9,800 | 9,750 | 9,750 | 9,700 | 7,720 | 7,840 | 7,792 | 7,728 | 7,784 | 6,473 | 6,533 | 6,467 | 6,500 | 6,467 | 5,657 | 5,554 | 5,531 | 5,514 | 5,571 | 4,925 | 4,860 | 4,865 | 4,870 | 4,825 | |
| 9,680 | 9,700 | 9,650 | 9,600 | 9,750 | 7,784 | 7,760 | 7,680 | 7,720 | 7,760 | 6,433 | 6,400 | 6,427 | 6,440 | 6,420 | 5,491 | 5,589 | 5,577 | 5,514 | 5,514 | 4,815 | 4,830 | 4,875 | 4,825 | 4,835 | |
| 9,720 | 9,720 | 9,720 | 9,710 | 9,710 | 7,768 | 7,768 | 7,776 | 7,776 | 7,776 | 6,471 | 6,471 | 6,460 | 6,480 | 6,487 | 5,554 | 5,549 | 5,549 | 5,549 | 5,560 | 4,865 | 4,865 | 4,863 | 4,845 | 4,848 | |
| 9,730 | 9,720 | 9,718 | 9,715 | 9,731 | 7,784 | 7,776 | 7,774 | 7,772 | 7,785 | 6,487 | 6,480 | 6,479 | 6,477 | 6,487 | 5,546 | 5,540 | 5,539 | 5,538 | 5,547 | 4,865 | 4,860 | 4,859 | 4,858 | 4,866 |
Выполнение задания
В лабораторной работе использованы методы расчета статистических значений, изложенные в практической работе «Основной метод повторяемости и воспроизводимости стандартного метода измерений» [2]. На основе формы А необходимо построить формы Б и В (табл. 1.2, 1.3).
В табл. 1.2 на каждом уровне измерений в каждой лаборатории приведены средние значения результатов измерений. В табл. 1.3 на каждом уровне измерений в каждой лаборатории приведены стандартные отклонения результатов измерений.
Таблица 1.2
Средние арифметические значения результатов
параллельных измерений по каждому уровню
| Форма В - Рекомендуемая форма для сопоставления исходных данных | |||||
| Лаборатория р (i) | Уровень q (j) | ||||
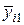
| 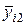
| 
| 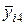
| 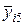
| |
| 9,750 | 7,773 | 6,488 | 5,565 | 4,869 | |
| 9,676 | 7,741 | 6,424 | 5,537 | 4,836 | |
| 9,716 | 7,773 | 6,474 | 5,552 | 4,857 | |
| 9,723 | 7,778 | 6,482 | 5,542 | 4,862 | |
Среднее значение 
| 9,716 | 7,766 | 6,467 | 5,549 | 4,856 |
Таблица 1.3
return false">ссылка скрытаСтандартные отклонения результатов параллельных измерений
| Форма C - Рекомендуемая форма для сопоставления исходных данных | |||||
| Лаборатория p (i) | Уровень q (j) | ||||
| si1 | si2 | si3 | si4 | si5 | |
| 0,0354 | 0,0495 | 0,0286 | 0,0556 | 0,0360 | |
| 0,0559 | 0,0410 | 0,0153 | 0,0432 | 0,0230 | |
| 0,0055 | 0,0044 | 0,0102 | 0,0049 | 0,0099 | |
| 0,0073 | 0,0058 | 0,0048 | 0,0041 | 0,0036 |
Проверка на два выброса в результатах измерения
Чтобы проверить, могут ли два наибольших результата наблюдений быть выбросами, вычисляют статистику Граббса
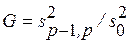 , (1.1)
, (1.1)
где
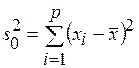 , (1.2)
, (1.2)
 , (1.3)
, (1.3)
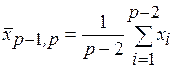 . (1.4)
. (1.4)
Соответственно, чтобы проверить два наименьших результата наблюдений, вычисляют статистику Граббса.
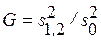 , (1.5)
, (1.5)
где
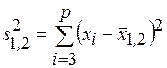 , (1.6)
, (1.6)
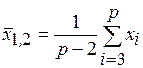 . (1.7)
. (1.7)
В каждой лаборатории на каждом уровне измерения получены ранжированные данные (табл. 1.4).
Таблица 1.4
Ранжирование результатов измерений в каждой лаборатории
| j | 1 лаборатория | 2 лаборатория | ||||||||
| x1 | x2 | x3 | x4=xn-1 | x5=xn | x1 | x2 | x3 | x4=xn-1 | x5=xn | |
| 9,700 | 9,750 | 9,750 | 9,750 | 9,800 | 9,600 | 9,650 | 9,680 | 9,700 | 9,750 | |
| 7,720 | 7,728 | 7,784 | 7,792 | 7,840 | 7,680 | 7,720 | 7,760 | 7,760 | 7,784 | |
| 6,467 | 6,467 | 6,473 | 6,500 | 6,533 | 6,400 | 6,420 | 6,427 | 6,433 | 6,440 | |
| 5,514 | 5,531 | 5,554 | 5,571 | 5,657 | 5,491 | 5,514 | 5,514 | 5,577 | 5,589 | |
| 4,825 | 4,860 | 4,865 | 4,870 | 4,925 | 4,815 | 4,825 | 4,830 | 4,835 | 4,875 | |
| j | 3 лаборатория | 4 лаборатория | ||||||||
| x1 | x2 | x3 | x4=xn-1 | x5=xn | x1 | x2 | x3 | x4=xn-1 | x5=xn | |
| 9,710 | 9,710 | 9,720 | 9,720 | 9,720 | 9,715 | 9,718 | 9,720 | 9,730 | 9,731 | |
| 7,768 | 7,768 | 7,776 | 7,776 | 7,776 | 7,772 | 7,774 | 7,776 | 7,784 | 7,785 | |
| 6,460 | 6,471 | 6,471 | 6,480 | 6,487 | 6,477 | 6,479 | 6,480 | 6,487 | 6,487 | |
| 5,549 | 5,549 | 5,549 | 5,554 | 5,560 | 5,538 | 5,539 | 5,540 | 5,546 | 5,547 | |
| 4,845 | 4,848 | 4,863 | 4,865 | 4,865 | 4,858 | 4,859 | 4,860 | 4,865 | 4,866 |
Критерий Граббса для двух выбросов применяют в следующих случаях.
1. Если при проверке с использованием критерия Граббса для одного выброса обнаруживается, что средние значения базовых элементов не имеют выбросов.
2. Анализ исходных данных в пределах базового элемента, для которого в результате проверки с использованием критерия Кохрена обнаруживается сомнительность значения стандартного отклонения.
Расчет статистик Граббса для двух выбросов результатов измерений представлен в табл. 1.5.
Таблица 1.5
Расчет статистик Граббса для двух выбросов
| j | 1 лаборатория | ||||||

| 
| 
| 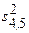
| 
| G1,2 | G4,5 | |
| 9,767 | 9,733 | 0,001667 | 0,001667 | 0,005000 | 0,3333 | 0,3333 | |
| 7,805 | 7,744 | 0,001835 | 0,002432 | 0,009805 | 0,1871 | 0,2480 | |
| 6,502 | 6,469 | 0,001806 | 0,000024 | 0,003276 | 0,5513 | 0,0073 | |
| 5,594 | 5,533 | 0,006098 | 0,000806 | 0,012377 | 0,4927 | 0,0651 | |
| 4,887 | 4,850 | 0,002217 | 0,000950 | 0,005170 | 0,4288 | 0,1838 | |
| j | 2 лаборатория | ||||||

| 
| 
| 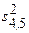
| 
| G1,2 | G4,5 | |
| 9,710 | 9,643 | 0,002600 | 0,003267 | 0,012520 | 0,2077 | 0,2609 | |
| 7,768 | 7,720 | 0,000384 | 0,003200 | 0,006733 | 0,0570 | 0,4753 | |
| 6,433 | 6,416 | 0,000085 | 0,000393 | 0,000938 | 0,0903 | 0,4186 | |
| 5,560 | 5,506 | 0,003246 | 0,000353 | 0,007478 | 0,4341 | 0,0472 | |
| 4,847 | 4,823 | 0,001217 | 0,000117 | 0,002120 | 0,5739 | 0,0550 | |
| j | 3 лаборатория | ||||||

| 
| 
| 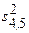
| 
| G1,2 | G4,5 | |
| 9,720 | 9,713 | 0,000000 | 0,000067 | 0,000120 | 0,0000 | 0,5556 | |
| 7,776 | 7,771 | 0,000000 | 0,000043 | 0,000077 | 0,0000 | 0,5556 | |
| 6,479 | 6,467 | 0,000129 | 0,000081 | 0,000419 | 0,3072 | 0,1926 | |
| 5,554 | 5,549 | 0,000061 | 0,000000 | 0,000095 | 0,6399 | 0,0000 | |
| 4,864 | 4,852 | 0,000003 | 0,000186 | 0,000389 | 0,0069 | 0,4784 | |
| j | 4 лаборатория | ||||||

| 
| 
| 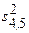
| 
| G1,2 | G4,5 | |
| 9,727 | 9,718 | 0,000074 | 0,000013 | 0,000211 | 0,3510 | 0,0601 | |
| 7,782 | 7,774 | 0,000049 | 0,000008 | 0,000141 | 0,3510 | 0,0601 | |
| 6,485 | 6,479 | 0,000033 | 0,000005 | 0,000088 | 0,3510 | 0,0601 | |
| 5,544 | 5,539 | 0,000029 | 0,000002 | 0,000070 | 0,3510 | 0,0601 | |
| 4,864 | 4,859 | 0,000021 | 0,000002 | 0,000053 | 0,3510 | 0,0601 |
Критические значения для критерия Граббса представлены в табл. 1.6.
В соответствии с данной таблицей можно сделать вывод, что лаборатории 2 и 4 не удовлетворяют критерию Граббса для двух выбросов на всех уровнях измерения. То есть два наибольших и два наименьших измеренных значения можно считать выбросами.
С помощью критерия Граббса для двух выбросов проверим, какие из лабораторий являются выпадающими, для чего повторим расчеты (1.1 – 1.7) применительно к средним значениям базовых элементов (табл. 1.7).
Таблица 1.6.
Критические значения для критерия Граббса
| j (k) | Одно наибольшее или одно наименьшее | Два наибольших или два наименьших | j (k) | Одно наибольшее или одно наименьшее | Два наибольших или два наименьших | ||||
| свыше 1% | свыше 5% | ниже 1% | ниже 5% | свыше 1% | свыше 5% | ниже 1% | ниже 5% | ||
| 1,155 | 1,155 | – | – | 3,060 | 2,758 | 0,3927 | 0,4711 | ||
| 1,496 | 1,481 | 0,0000 | 0,0002 | 3,087 | 2,781 | 0,4085 | 0,4857 | ||
| 1,764 | 1,715 | 0,0018 | 0,0090 | 3,112 | 2,802 | 0,4234 | 0,4994 | ||
| 1,973 | 1,887 | 0,0116 | 0,0349 | 3,135 | 2,822 | 0,4376 | 0,5123 | ||
| 2,139 | 2,020 | 0,0308 | 0,0708 | 3,157 | 2,841 | 0,4510 | 0,5245 | ||
| 2,274 | 2,126 | 0,0563 | 0,1101 | 3,178 | 2,859 | 0,4638 | 0,5360 | ||
| 2,387 | 2,215 | 0,0851 | 0,1492 | 3,199 | 2,876 | 0,4759 | 0,5470 | ||
| 2,482 | 2,290 | 0,1150 | 0,1864 | 3,218 | 2,893 | 0,4875 | 0,5574 | ||
| 2,564 | 2,355 | 0,1448 | 0,2213 | 3,236 | 2,908 | 0,4985 | 0,5672 | ||
| 2,636 | 2,412 | 0,1738 | 0,2537 | 3,253 | 2,924 | 0,5091 | 0,5766 | ||
| 2,699 | 2,462 | 0,2016 | 0,2836 | 3,270 | 2,938 | 0,5192 | 0,5856 | ||
| 2,755 | 2,507 | 0,2280 | 0,3112 | 3,286 | 2,952 | 0,5288 | 0,5941 | ||
| 2,806 | 2,549 | 0,2530 | 0,3367 | 3,301 | 2,965 | 0,5381 | 0,6023 | ||
| 2,852 | 2,585 | 0,2767 | 0,3603 | 3,316 | 2,979 | 0,5469 | 0,6101 | ||
| 2,894 | 2,620 | 0,2990 | 0,3822 | 3,330 | 2,991 | 0,5554 | 0,6175 | ||
| 2,932 | 2,651 | 0,3200 | 0,4025 | 3,343 | 3,003 | 0,5636 | 0,6247 | ||
| 2,968 | 2,681 | 0,3398 | 0,4214 | 3,356 | 3,014 | 0,5714 | 0,6316 | ||
| 3,001 | 2,709 | 0,3585 | 0,4391 | 3,369 | 3,025 | 0,5789 | 0,6382 | ||
| 3,031 | 2,733 | 0,3761 | 0,4556 | 3,381 | 3,036 | 0,5862 | 0,6445 |
Таблица 1.7
Расчет статистик Граббса для определения выпадающих лабораторий
| j | 
| 
| 
| 
| 
| G1,2 | G3,4 |
| 9,736 | 9,696 | 0,000370 | 0,000800 | 0,002802 | 0,1320 | 0,2855 | |
| 7,776 | 7,757 | 0,000015 | 0,000512 | 0,000876 | 0,0166 | 0,5843 | |
| 6,485 | 6,449 | 0,000018 | 0,001240 | 0,002561 | 0,0070 | 0,4842 | |
| 5,559 | 5,540 | 0,000087 | 0,000012 | 0,000472 | 0,1845 | 0,0265 | |
| 4,865 | 4,847 | 0,000027 | 0,000225 | 0,000602 | 0,0455 | 0,3734 |
Согласно статистикам Граббса все лаборатории являются выпадающими и результаты измерений не могут быть использованы для получения статистически значимого результата.
Расчет общего среднего значения и дисперсий
Метод анализа включает в себя нахождение оценки общего среднего m и прецизионности для каждого уровня отдельно.
Для уровня j общее среднее значение
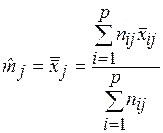 . (1.8)
. (1.8)
Для каждого уровня рассчитывают дисперсии: повторяемости 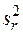 , межлабораторные
, межлабораторные 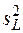 и воспроизводимости
и воспроизводимости 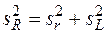 .
.
Дисперсия повторяемости
 . (1.9)
. (1.9)
Межлабораторная дисперсия
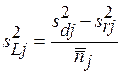 , (1.10)
, (1.10)
где
 , (1.11)
, (1.11)
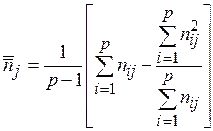 . (1.12)
. (1.12)
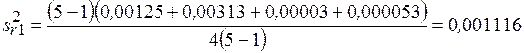 ;
;
 = 0,001047;
= 0,001047; 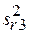 = 0,000295;
= 0,000295;  = 0,001251;
= 0,001251; 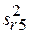 = 0,000483.
= 0,000483.
 .
.
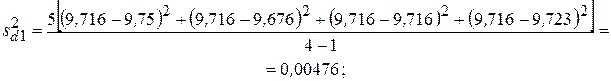
 = 0,00146;
= 0,00146;  = 0,004269;
= 0,004269; 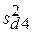 = 0,000787;
= 0,000787;  = 0,001003.
= 0,001003.
Если в результате расчета межлабораторной дисперсии получено отрицательное значение, то 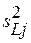 следует принять равным нулю.
следует принять равным нулю.
 ;
;
 = 0,000083;
= 0,000083;  = 0,000795;
= 0,000795;  = 0,000000;
= 0,000000; 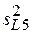 = 0,000104.
= 0,000104.
Дисперсия воспроизводимости
 (1.13)
(1.13)
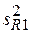 = 0,001116 + 0,000711 = 0,001827;
= 0,001116 + 0,000711 = 0,001827;
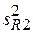 = 0,00113;
= 0,00113;  = 0,00109;
= 0,00109; 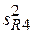 = 0,001251;
= 0,001251; 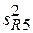 = 0,000587.
= 0,000587.
Результаты расчета представлены для каждого значения j в табл. 1.8.
Таблица 1.8.
Расчет показателей прецизионности
| j | 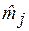
| 
| 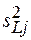
| 
|
| 9,716 | 0,001116 | 0,000711 | 0,001827 | |
| 7,766 | 0,001047 | 0,000083 | 0,001130 | |
| 6,467 | 0,000295 | 0,000795 | 0,001090 | |
| 5,549 | 0,001251 | 0,000000 | 0,001251 | |
| 4,856 | 0,000483 | 0,000104 | 0,000587 |
Установление функциональной зависимости между значениями прецизионности и средним значением m для уровня измерения
Существует регулярная функциональная связь между прецизионностью и средним значением для уровня m. Эта связь относится как к стандартным отклонениям повторяемости, так и воспроизводимости. Для удобства простановки подстрочного индекса уровня j, обозначение sr или sR сокращено просто до s Ниже рассмотрены три типа соотношений применительно к стандартным отклонениям sr или sR:
I s = bm (прямая линия, проходящая через начало координат);
II s = a + bm (прямая линия, проходящая выше начала координат);
III lg s = c + d lgm (или s = Cmd); d £ 1 (экспоненциальная зависимость).
При d > 0 зависимости I и III будут сводиться к s = 0 для m = 0.
При a = 0 и d = 1 все три зависимости являются тождественными, предпочтение должно быть отдано зависимости I.
Для зависимостей I и II рекомендуется методика, изложенная в пункте 1, а для зависимости III – методика, изложенная в пункте 2.
Аппроксимация прямой линией осложняется тем, что  и sj являются оценками и, следовательно, подвержены ошибкам. Однако поскольку угловой коэффициент b обычно невелик (порядка 0,1 или менее), то ошибки в оценке
и sj являются оценками и, следовательно, подвержены ошибкам. Однако поскольку угловой коэффициент b обычно невелик (порядка 0,1 или менее), то ошибки в оценке  имеют небольшое влияние и на окончательный результат в большей степени влияют ошибки в оценке s.
имеют небольшое влияние и на окончательный результат в большей степени влияют ошибки в оценке s.
1. При аппроксимации зависимости s = f(  ) прямой линией весовые коэффициенты должны быть пропорциональны
) прямой линией весовые коэффициенты должны быть пропорциональны 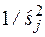 , где
, где  представляет собой прогнозируемое стандартное отклонение повторяемости или стандартное отклонение воспроизводимости для уровня j.
представляет собой прогнозируемое стандартное отклонение повторяемости или стандартное отклонение воспроизводимости для уровня j.
При весовых коэффициентах Wj, равных 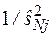 расчетные формулы
расчетные формулы
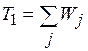 ,
,  ,
,  ,
, 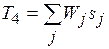 ,
, 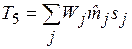 , (1.14)
, (1.14)
где N = 0, 1, 2 ... для последовательных итераций.
Начальные значения  представляют собой исходные значения sj.
представляют собой исходные значения sj.
Для зависимости I (s = bm)
b = T5/T3. (1.15)
Для одной и той совокупности данных приведены расчеты тремя методами. Результаты расчета I методом (1.14, 1.15) приведены в табл. 1.9.
Возможен расчет коэффициента b без итераций, когда использование весовых коэффициентов  , где
, где 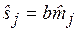 , приводит к упрощенному выражению:
, приводит к упрощенному выражению:
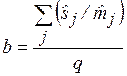 , (1.16)
, (1.16)
где q – количество уровней измеряемой характеристики.
Результаты определения зависимостей s = f(  ) методом итераций и упрощенным методом представлены на рис. 1.1, где обозначения прямых линий, рассчитанных методом итераций имеют дополнительный индекс I.
) методом итераций и упрощенным методом представлены на рис. 1.1, где обозначения прямых линий, рассчитанных методом итераций имеют дополнительный индекс I.
Таким образом для метода итераций sr = 0,003596× 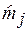 , sR = 0,004858×
, sR = 0,004858× 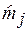 ; для упрощенного метода sr = 0,004232×
; для упрощенного метода sr = 0,004232× 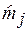 , sR = 0,005039×
, sR = 0,005039× 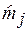 .
.
Таблица 1.9
Аппроксимация зависимости s = f(  ) прямой линией методом I
) прямой линией методом I
| Стандартное отклонение повторяемости | |||||||
| Итерация 1 | Коэффициент | sr1 | sr2 | sr3 | sr4 | sr5 | |
| 0,033402 | 0,032360 | 0,017177 | 0,035373 | 0,021983 | |||
| W1 | W2 | W3 | W4 | W5 | |||
| 896,3 | 954,9 | 3389,3 | 799,2 | 2069,3 | |||
| Т1 | Т2 | Т3 | Т4 | Т5 | |||
| – | – | 357359,7 | – | 1285,1 | |||
| b | 0,003596 | ||||||
| Итерация 2 | sr1 | sr2 | sr3 | sr4 | sr5 | ||
| 0,034941 | 0,027929 | 0,023256 | 0,019956 | 0,017463 | |||
| W1 | W2 | W3 | W4 | W5 | |||
| 819,1 | 1282,0 | 1848,9 | 2511,1 | 3279,2 | |||
| Т1 | Т2 | Т3 | Т4 | Т5 | |||
| – | – | 386617,6 | – | 1390,4 | |||
| b | 0,003596 | ||||||
| Итерация 3 | sr1 | sr2 | sr3 | sr4 | sr5 | ||
| 0,034941 | 0,027929 | 0,023256 | 0,019956 | 0,017463 | |||
| W1 | W2 | W3 | W4 | W5 | |||
| 819,1 | 1282,0 | 1848,9 | 2511,1 | 3279,2 | |||
| Т1 | Т2 | Т3 | Т4 | Т5 | |||
| – | – | 386617,6 | – | 1390,4 | |||
| b | 0,003596 | ||||||
| Стандартное отклонение воспроизводимости | |||||||
| Итерация 1 | sR1 | sR2 | sR3 | sR4 | sR5 | ||
| 0,042738 | 0,033613 | 0,033012 | 0,035373 | 0,024232 | |||
| W1 | W2 | W3 | W4 | W5 | |||
| 547,5 | 885,1 | 917,6 | 799,2 | 1703,0 | |||
| Т1 | Т2 | Т3 | Т4 | Т5 | |||
| – | – | 208208,7 | – | 1011,6 | |||
| b | 0,004858 | ||||||
| Итерация 2 | sR1 | sR2 | sR3 | sR4 | sR5 | ||
| 0,047205 | 0,037731 | 0,031419 | 0,026960 | 0,023592 | |||
| W1 | W2 | W3 | W4 | W5 | |||
| 448,8 | 702,4 | 1013,0 | 1375,8 | 1796,7 | |||
| Т1 | Т2 | Т3 | Т4 | Т5 | |||
| – | – | 211832,1 | – | 1029,2 | |||
| b | 0,004858 | ||||||
| Итерация 3 | sR1 | sR2 | sR3 | sR4 | sR5 | ||
| 0,047205 | 0,037731 | 0,031419 | 0,026960 | 0,023592 | |||
| W1 | W2 | W3 | W4 | W5 | |||
| 448,8 | 702,4 | 1013,0 | 1375,8 | 1796,7 | |||
| Т1 | Т2 | Т3 | Т4 | Т5 | |||
| – | – | 211832,1 | – | 1029,2 | |||
| B | 0,004858 | ||||||

Рис. 1.1. Графики зависимостей s = f(  ) для I метода
) для I метода
Для зависимости II (s = a + bm)
 , (1.17)
, (1.17)
 . (1.18)
. (1.18)
Начальными значениями  являются исходные значения s. Их используют для расчета
являются исходные значения s. Их используют для расчета  (j = 1, 2, …, q) и вычисления a1 и b1 по формулам (1.14), (1.17), (1.18) и определения
(j = 1, 2, …, q) и вычисления a1 и b1 по формулам (1.14), (1.17), (1.18) и определения  .
.
Затем расчеты повторяют для  с целью получения
с целью получения  . Итеративный подход позволяет исключить грубые ошибки в весах, и равенство для
. Итеративный подход позволяет исключить грубые ошибки в весах, и равенство для  необходимо рассматривать в качестве окончательного результата.
необходимо рассматривать в качестве окончательного результата.
Результаты определения зависимостей s = f(  ) методом итераций представлены в табл. 1.10. Графики зависимостей приведены на рис. 1.2.
) методом итераций представлены в табл. 1.10. Графики зависимостей приведены на рис. 1.2.
Для метода II sr = 0,010097×+ 0,002112 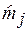 , sR = 0,011112×+ 0,003213
, sR = 0,011112×+ 0,003213 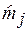 .
.
Таблица 1.10
Аппроксимация зависимости s = f(  ) прямой линией методом II
) прямой линией методом II
| Стандартное отклонение повторяемости | ||||||||
| Итерация 1 | sr1 | sr2 | sr3 | sr4 | sr5 | |||
| 0,033402 | 0,032360 | 0,017177 | 0,035373 | 0,021983 | ||||
| W1 | W2 | W3 | W4 | W5 | ||||
| 896,3 | 954,9 | 3389,3 | 799,2 | 2069,3 | ||||
| Т1 | Т2 | Т3 | Т4 | Т5 | ||||
| 8109,0 | 52526,5 | 357359,7 | 192,8 | 1285,1 | ||||
| а | 0,010097 | b | 0,002112 | |||||
| Итерация 2 | sr1 | sr2 | sr3 | sr4 | sr5 | |||
| 0,030619 | 0,026500 | 0,023756 | 0,021817 | 0,020353 | ||||
| W1 | W2 | W3 | W4 | W5 | ||||
| 1066,7 | 1424,0 | 1772,0 | 2100,9 | 2414,0 | ||||
| Т1 | Т2 | Т3 | Т4 | Т5 | ||||
| 8777,5 | 56262,6 | 382305,9 | 207,5 | 1375,6 | ||||
| а | 0,010097 | b | 0,002112 | |||||
| Итерация 3 | sr1 | sr2 | sr3 | sr4 | sr5 | |||
| 0,030619 | 0,026500 | 0,023756 | 0,021817 | 0,020353 | ||||
| W1 | W2 | W3 | W4 | W5 | ||||
| 1066,7 | 1424,0 | 1772,0 | 2100,9 | 2414,0 | ||||
| Т1 | Т2 | Т3 | Т4 | Т5 | ||||
| 8777,5 | 56262,6 | 382305,9 | 207,5 | 1375,6 | ||||
| а | 0,010097 | b | 0,002112 | |||||
| Стандартное отклонение воспроизводимости | ||||||||
| Итерация 1 | sR1 | sR2 | sR3 | sR4 | sR5 | |||
| 0,042738 | 0,033613 | 0,033012 | 0,035373 | 0,024232 | ||||
| W1 | W2 | W3 | W4 | W5 | ||||
| 547,5 | 885,1 | 917,6 | 799,2 | 1703,0 | ||||
| Т1 | Т2 | Т3 | Т4 | Т5 | ||||
| 4852,4 | 30831,8 | 208208,7 | 153,0 | 1011,6 | ||||
| а | 0,011112 | b | 0,003213 | |||||
| Итерация 2 | sR1 | sR2 | sR3 | sR4 | sR5 | |||
| 0,042329 | 0,036064 | 0,031890 | 0,028941 | 0,026714 | ||||
| W1 | W2 | W3 | W4 | W5 | ||||
| 558,1 | 768,9 | 983,3 | 1193,9 | 1401,1 | ||||
| Т1 | Т2 | Т3 | Т4 | Т5 | ||||
| 4905,6 | 31183,3 | 209995,3 | 154,7 | 1021,2 | ||||
| а | 0,011112 | b | 0,003213 | |||||
| Итерация 3 | sR1 | sR2 | sR3 | sR4 | sR5 | |||
| 0,042329 | 0,036064 | 0,031890 | 0,028941 | 0,026714 | ||||
| W1 | W2 | W3 | W4 | W5 | ||||
| 558,1 | 768,9 | 983,3 | 1193,9 | 1401,1 | ||||
| Т1 | Т2 | Т3 | Т4 | Т5 | ||||
| 4905,6 | 31183,3 | 209995,3 | 154,7 | 1021,2 | ||||
| а | 0,011112 | b | 0,003213 | |||||

Рис. 1.2. Графики зависимостей s = f(  ) для II метода
) для II метода
2. Для зависимости III расчетные формулы выглядят следующим образом:
 ,
,  ,
,  ,
,  , (1.19)
, (1.19)
 , (1.20)
, (1.20)
 . (1.21)
. (1.21)
Аналогично I и II методу начальными значениями  являются исходные значения s. Их используют для вычисления c1 и d1 по формулам (1.19), (1.20), (1.21) и определения
являются исходные значения s. Их используют для вычисления c1 и d1 по формулам (1.19), (1.20), (1.21) и определения  .
.
Затем расчеты повторяют для  с целью получения
с целью получения  . Равенство для
. Равенство для  необходимо рассматривать в качестве окончательного результата.
необходимо рассматривать в качестве окончательного результата.
Результаты определения зависимостей s = f(  ) методом итераций представлены в табл. 1.11. Графики зависимостей приведены на рис. 1.3.
) методом итераций представлены в табл. 1.11. Графики зависимостей приведены на рис. 1.3.
Таблица 1.11
Аппроксимация зависимости s = f(  ) методом III
) методом III
| Стандартное отклонение повторяемости | ||||||||
| Итерация 1 | lgm1 | lgm2 | lgm3 | lgm4 | lgm5 | |||
| 0,9875 | 0,8902 | 0,8107 | 0,7442 | 0,6863 | ||||
| lgsr1 | lgsr2 | lgsr3 | lgsr4 | lgsr5 | ||||
| –1,476231 | –1,489985 | –1,765052 | –1,451328 | –1,657914 | ||||
| Т1 | Т2 | Т3 | Т4 | – | ||||
| 4,1189 | 3,4497 | –7,8405 | –6,4330 | – | ||||
| c | –1,944410 | d | 0,456807 | |||||
| Итерация 2 | lgm1 | lgm2 | lgm3 | lgm4 | lgm5 | |||
| 0,9875 | 0,8902 | 0,8107 | 0,7442 | 0,6863 | ||||
| lgsr1 | lgsr2 | lgsr3 | lgsr4 | lgsr5 | ||||
| –1,514014 | –1,576756 | –1,624230 | –1,661199 | –1,691368 | ||||
| Т1 | Т2 | Т3 | Т4 | – | ||||
| 4,1189 | 3,4497 | –8,0676 | –6,6125 | – | ||||
| c | –2,099001 | d | 0,589341 | |||||
| Итерация 3 | lgm1 | lgm2 | lgm3 | lgm4 | lgm5 | |||
| 0,9875 | 0,8902 | 0,8107 | 0,7442 | 0,6863 | ||||
| lgsr1 | lgsr2 | lgsr3 | lgsr4 | lgsr5 | ||||
| –1,514014 | –1,576756 | –1,624230 | –1,661199 | –1,691368 | ||||
| Т1 | Т2 | Т3 | Т4 | – | ||||
| 4,1189 | 3,4497 | –8,0676 | –6,6125 | – | ||||
| c | –2,099001 | d | 0,589341 | |||||
| Стандартное отклонение воспроизводимости | ||||||||
| Итерация 1 | lgm1 | lgm2 | lgm3 | lgm4 | lgm5 | |||
| 0,9875 | 0,8902 | 0,8107 | 0,7442 | 0,6863 | ||||
| lgsR1 | lgsR2 | lgsR3 | lgsR4 | lgsR5 | ||||
| –1,369182 | –1,473490 | –1,481330 | –1,451328 | –1,615608 | ||||
| Т1 | Т2 | Т3 | Т4 | – | ||||
| 4,1189 | 3,4497 | –7,3909 | –6,0536 | – | ||||
| c | –1,986780 | d | –0,617389 | |||||
| Итерация 2 | lgm1 | lgm2 | lgm3 | lgm4 | lgm5 | |||
| 0,9875 | 0,8902 | 0,8107 | 0,7442 | 0,6863 | ||||
| lgsR1 | lgsR2 | lgsR3 | lgsR4 | lgsR5 | ||||
| –1,373362 | –1,442929 | –1,496352 | –1,538491 | –1,573269 | ||||
| Т1 | Т2 | Т3 | Т4 | – | ||||
| 4,1189 | 3,4497 | –7,4244 | –6,0785 | – | ||||
| c | –2,032091 | d | 0,664268 | |||||
| Итерация 3 | lgm1 | lgm2 | lgm3 | lgm4 | lgm5 | |||
| 0,9875 | 0,8902 | 0,8107 | 0,7442 | 0,6863 | ||||
| lgsR1 | lgsR2 | lgsR3 | lgsR4 | lgsR5 | ||||
| –1,373362 | –1,442929 | –1,496352 | –1,538491 | –1,573269 | ||||
| Т1 | Т2 | Т3 | Т4 | – | ||||
| 4,1189 | 3,4497 | –7,4244 | –6,0785 | – | ||||
| c | –2,032091 | d | 0,664268 | |||||
На рис. 1.3. изображены зависимости логарифмов стандартных отклонений от логарифмов средних арифметических значений на каждом уровне измерений  ,
,  .
.

Рис. 1.2. Графики зависимостей s = f(  ) для III метода
) для III метода
Статистический анализ как поэтапная процедура
Статистический анализ данных по результатам многоуровневого эксперимента можно представить как поэтапную процедуру (рис. 1.4).
Этап 1. Строят график функции sj по аргументу  и на его основе делают вывод, зависит ли s от m или нет. Если s признают зависящим от m, пренебрегают этапом 2 и приступают к этапу 3. Если s оценивают как не зависящее от m, приступают к этапу 2.
и на его основе делают вывод, зависит ли s от m или нет. Если s признают зависящим от m, пренебрегают этапом 2 и приступают к этапу 3. Если s оценивают как не зависящее от m, приступают к этапу 2.
Этап 2. Используют выражение  для окончательной оценки значения стандартного отклонения повторяемости. Пренебрегая этапами 3 – 6 приступают непосредственно к этапу 7.
для окончательной оценки значения стандартного отклонения повторяемости. Пренебрегая этапами 3 – 6 приступают непосредственно к этапу 7.
Этап 3. Исходя из графика функции sj по аргументу  , делают вывод, может ли зависимость между s и m быть выражена прямой линией, и если да, то является ли подходящей зависимость I (s = bm) или II (s = a + bm).
, делают вывод, может ли зависимость между s и m быть выражена прямой линией, и если да, то является ли подходящей зависимость I (s = bm) или II (s = a + bm).
