Проверка гипотезы о числовом значении математического ожидания нормально распределенной случайной величины при неизвестной дисперсии

 

Пусть случайная величина Х распределена по нормальному закону с параметрами а и s, т.е. . Причем параметры и неизвестны. Пусть по результатам n независимых наблюдений найдены выборочная средняя и исправленное среднее квадратическое отклонение . Требуется при заданном уровне значимости a проверить основную гипотезу . Конкурирующая гипотеза может быть сформулирована одним из следующих способов: 1) ; 2) ; 3) . В качестве статистического критерия рассматривается случайная величина . Случайная величина Т при условии справедливости основной гипотезы распределена по закону Стьюдента с числом степеней свободы. Принцип проверки гипотезы 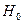такой же, как в предыдущем параграфе, поэтому укажем только порядок проверки гипотезы.

Случай 1.

.

Порядок проверки:

1) находим наблюдаемое значение критерия по формуле , где и - вычисленные по выборке выборочная средняя и исправленное среднее квадратическое отклонение;

2) по таблице критических точек распределения Стьюдента, по заданному уровню значимости a и по числу степеней свободы находим критическую точку (так как конкурирующая гипотеза имеет вид , то критическая область – двусторонняя);

3) если , то основную гипотезу отвергаем в пользу конкурирующей гипотезы . Если - нет оснований отвергнуть гипотезу .

Случай 2. .

Случай 3. .

В случаях 2 и 3 проверка гипотезы осуществляется точно также как в случае 1 за исключением того, что для нахождения критической точки используется односторонняя (правосторонняя) критическая область.