Виды зависимостей. Корреляционный анализ.

Оператор Если заданы два произвольных множества Sx и Sy и дан закон, в соответствии с которым любому x будет соответствовать вполне определенный y , то говорят, что задан оператор.
Функция, Функционал и Оператор – отражают действие причинно-следственной связи.
Стохастическая связь - это такая зависимость, при которой определенному значению x будет соответствовать множество y.
x (y1, y2, y3,..., yn)

Корреляционный анализ
Имеется n случайных величин х1,х2,…хn
Корреляционный момент (ковариация) или момент связи
Кхуназывают второй смешанный центральный момент, т.е. матем. ожидание произведения центрированных в-н

х°=x-mxи y°=y-my.
Kxy=M[(x-mx)(y-my)]
Коэффициентом корреляции случайных величин Х и У называется мат. ожидание произведения стандартных случайных величин
rxy=M[((x-mx)/σx)((y-my)/σy)]
rxy=Kxy/(σxσy)
коэффициент корреляции характеризует степень тесноты линейной стохастической связи между случайными величинами

положительная отрицательная

корреляция корреляция

линейная регрессия

Корреляционный анализ изучает на основании выборки стохастическую зависимость между случайными переменными.
Для коэффициента корреляции ρ двух случайных величин х и у справедливо:
1) -1≤ρ≤1
2) при ρ=±1 имеется функциональная связь, т.е. все точки лежат на прямой
3) если ρ=0, то х и у –некоррелированы (но это не говорит об отсутствии связи. Две независимые случайные переменные всегда некоррелированы, но некоррелированные переменные необязательно независимы)
Параметр ρ оценивается с помощью: 1) выборочного коэффициента корреляции 2) частного коэффициента корреляции 3) множественного коэффициента корреляции 4) коэффициента корреляции по Спирмэну
5) квадратного коэффициента корреляции и углового критерия 6) коэффициента сопряженности 7) корреляционного отношения

1. Коэффициент корреляции оценивается

наличие корреляции, т.е. гипотеза о том, может ли выборочный коэф. корреляции иметь случайные отклонения от нуля при генеральной совокупности с параметром ρ=0, проверяется на основании t-распределения с (n-2) степенями свободы
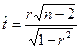если гипотеза Н0: ρ=0 отклоняется.
Для оценки коэффициента корреляции можно воспользоваться и статистикой подчиненной F- распр. Проверку разности между r и ρ можно осуществить статистикой подчиненной нормальному закону распределения.
2. Частные (парциальные) коэф. корреляции характеризуют тесноту связи между двумя случайными величинами системы при исключении влияния остальных случайных величин.
Частный коэф. корреляции в-н Х1и Х2, входящих в систему {Х1,Х2…Хn} относительно в-н Х3, Х4, …Хnобозначается через r12,34…n

где Р12- минор детерминанта квадратной матрицы (матрицы коэф. корреляции), получаемой путем вычеркивания 1ойстроки и 2гостолбца, умноженной на (-1)1+2=-1

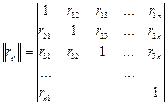
В отличие от коэф. множеств. корреляции коэф. частной корреляции как коэф. парной корреляции меняется в пределах от -1 до +1.
Пи наличии корреляции частный коэф. корреляции r12,34…nв общем случае не равен коэф. парной корреляции r12.

3. Коэффициент множественной корреляции. (сводный коэф. корреляции)
Используется для описания системы сл. в-н {Х1,Х2…Хn}. Служит характеристикой корреляции между величиной Х1с одной стороны и всей совокупностью величин (Х2,Х3…Хn) с другой.
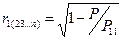Р – детерминант квадратной матрицы коэф. коррел.

Р11– минор этого детерминанта

При n=3

Свойства
1. всегда является положительным числом 0≤r1(23..n)≤1
2. при r1(23..n)=1 случайная величина Х1почти наверное равна линейной комбинации Х2,Х3…Хn.
3. равенство r1(23..n)=0 имеет место тогда, когда r12,r13,…r1n=0, т.е. случайная величина Х1не коррелированна со всеми остальными случайными величинами системы.

4.Корреляционное отношение.
Применение коэф. корреляции ограничивается случаем линейной связи. Для оценки нелинейной связи используют корреляционное отношение. Корреляционное отношение требует расчета условных дисперсий.
Зависимость Dу׀х= φ(х) – скедастическая функция. Если φ(х)=const, то условная дисперсия переменной У –постоянна, не зависит от х и говорят, что связь между случайными переменными у и х гомоскедастическая.
Чтобы получить представление о рассеянии случайной переменной у во всем диапазоне изменения переменной Х1используют вероятностную, называемую средней условной дисперсией 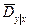. По гомоскедастической связи, когда Dу׀х=const, то 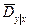ничем не отличается от Dу׀х. По определению

Установим соотношение между полной дисперсией Dyи средней условной дисперсией 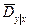. Формула полной дисперсии случайной переменной у записывается в виде
Dy= M[ y2]-m2y, my= M[y]
Cделаем искусственное преобразование. Прибавим и отнимем от правой части M[m2ylx], где mylx= M[y l x] -условное мат.ожидание
Dy= M[ y2 ] - M[m2ylx] + M[m2ylx] - m2y

Вспомним, что 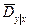= M[ y2] - M[ m2ylx]
M[m2ylx] - m2y= D{M[ylx]}
Это следует из D{M[ylx]} = D[mylx] = M[m2ylx] - {M[mylx]}2 = M[m2ylx]-m2y,
т.е. Dy= 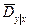+ D{M[ylx]} Это формула разбиения дисперсий.

Т.е. полная дисперсия является суммой средней условной дисперсии и дисперсии условного математического ожидания. Поясним это.
Если х – входная, а у – выходная переменные, то дисперсия условного мат. ожидания D{M[ylx]} представляет собой ту часть полной дисперсии Dyвыходной переменной у, которая связана с влиянием входной переменной х.
Вторая часть полной дисперсии – средняя условная дисперсия – определяется влиянием совокупности всех остальных переменных, кроме учтенной переменной х.
Так как 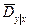= Dy– D{M[ylx]} , то 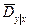≤Dy
Равенство имеет место, когда D{M[ylx]} = 0
В качестве меры корреляц. отношения принято η2yx=1 - 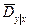/ Dy ; ηyx– корреляц. отношение

Свойства: 1. 0 ≤ ηyx≤ 1 ; 0 ≤ ηxy≤1. Это свойство следует из формул
ηyx=1- 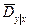/Dy ηxy= 1- 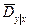/Dx
аналогично
η2yx= D{ M[ylx] } / Dy η2xy= D{ М[xly] } / Dx
2. Величина η всегда положительна.
3. Равенство ηyx= 0 означает, что переменная y не коррелированна с переменной x. Если x и y – независимы, то ηyx= 0.
4. Равенство ηyx=1 соответствует функциональной связи между y и x.
5. В общем случае ηyx≠ ηxy, т.е. данная связь несимметрична

6. Если связь между переменными x и y линейна, то ηyx= ηxy.
7. При линейной регресии ηyx= ׀ryx׀, т.е. корреляционное отношение служит характеристикой и линейной связи.
8. При линейной регрессии всегда ηyx> ׀ryx׀, т.е. коэффициент корреляции при нелинейной стохастической связи дает заниженные оценки.
Разность η2yx-r2yx=h2yx– индикатор степени нелинейности стохастической связи.

5.Классификация задач управления и идентификация систем.

1. Задачи детерминированного управления.

u(t)=? y(t) z(t)

Объект М

М - измерительное устройство

Дано Соотношения между z(t) и y(t) и между y(t) и u(t) .

Цель Найти такое управление u(t), чтобы y(t) или z(t) были бы как можно ближе к желаемому.

2. Задачи оценки.
V(t)
W(t) y(t) z(t)
Объект М
W(t) - вектор действующих на систему шумов.
V(t) - вектор шумов измерений.
Дано Соотношения между z(t) и y(t), V(t)
y(t) и W(t) ;
Статистическое описание V(t) и W(t).
Проводятся замеры на некотором интервале времени Т.
t - текущее время; t = T - задача фильтрации; t > T - задача предсказания или прогнозирования;
t < T - задача сглаживания;
Цель Найти такие оценки 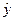(t½T), которые являются лучшими в некотором смысле.

3.Задача стохастического управления.

W(t) V(t)
u(t)=? y(t) z(t)
Объект М

Дано Соотношения между z(t) и y(t), V(t)
y(t) и u(t), W(t);
Статистическое описание V(t) и W(t).
Цель Найти такое управление u(t), чтобы некоторая оценка 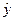(t) была близка к желаемому.

4. Задача идентификации.

W(t) V(t)

u(t) y(t) z(t)
Объект ? М

Дано Соотношения между z(t) и y(t), V(t)
Статистическое описание V(t) и W(t).
Измеряются z(t) и u(t)
Цель Определить лучшую в некотором смысле модель объекта.

5. Задача адаптивного управления.

W(t) V(t)

u(t)=? y(t) z(t)
Объект ? М
Дано Соотношения между z(t) и y(t), V(t)
Статистическое описание V(t) и W(t).
Измеряются z(t) и u(t)
Цель Определить u(t), для которого некоторая оценка y(t) была бы близка к желаемому.

Иерархия моделей.

Экономические модели оптимизационные

Обработка информации и управления задачи
Физико-химические модели процессов

Методология построения детерминированных моделей

Структура

ошибка ошибка ошибка

моделирования линеаризации агрегирования

Дифференциальные Дифференциальные
уравнения в частных уравнения в частных
производных производных ОДУ
(нелинейные) (линейные)

линеаризация агрегирование

Информация о структуре (априорная)
Объект Модель
Информация об измерениях (апостериорная)

Ст Оценивание порядка
Данные Кванто- ру
измере- вание к Оценивание параметров
ний ту
ра Оценивание состояний

обработка
ошибка ошибка
измерения квантования