Силы в зубчатом зацеплении

 

Фактически, движение передаётся зубчатым зацеплением посредством силы нормального давления в точке контакта зубьев Fn , которая определяется, как интеграл от контактных напряжений sк по всей площади S контакта зубьев Fn = ∫s(sк)dS.

Однако этот интеграл вычислить практически невозможно, т.к. неизвестен точный вид функции sк.

Используют другой приём: ещё неизвестную силу нормального давления Fn сначала раскладывают на три ортогональных проекции:

è осевую силу Fa , направленную параллельно оси колеса;

è радиальную силу Fr , направленную по радиусу к центру колеса;

è окружную силу Ft , направленную касательно к делительной окружности.

Легче всего вычислить силу Ft , зная передаваемый вращающий момент Мвр и делительный диаметр dw

Ft = 2MВр / dw.

Радиальная сила вычисляется, зная угол зацепления aw

Fr = Ft tgaw.

Осевая сила вычисляется через окружную силу и угол наклона зубьев b

Fa = Ft tgb.

Наконец, если необходимо, зная все проекции, можно вычислить и модуль нормальной силы Fn= (Fa2 + Fr2 + Ft2)½ = Ft /(cosαw cosβ).

Нормальная сила распределена по длине контактной линии, поэтому, зная длинуlSконтактной линии,можно вычислить удельную погонную нормальную нагрузку qn = Fn / lΣ ≈ Ft /(b εαkε cosαw cosβ),

где ea - коэффициент перекрытия, ke - отношение минимальной длины контактной линии к средней.

Для двух цилиндрических колёс в зацеплении одноимённые силы равны, но противоположны. Окружная сила для шестерни противоположна направлению вращения, окружная сила для колеса направлена в сторону вращения.

Расчёт зубьев на контактную выносливость

 

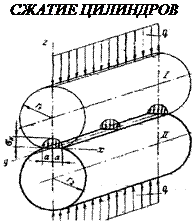Аналитическими методами теории прочности можно получить точное решение для вычисления напряжений в контакте двух эвольвентных профилей. Однако это слишком усложнит задачу, поэтому на малой площадке контакта геометрия эвольвентных профилей корректно подменяется контактом двух цилиндров. Для этого случая используют формулу Герца-Беляева:

Здесь Епр – приведённый модуль упругости материалов шестерни и колеса

Епр = 2 Е1 Е2 / ( Е1 + Е2),

rпр – приведённый радиус кривизны зубьев

1/rпр = 1/r1 ± 1/r2, r1,2 = 0,5dW 1,2 sin aW ,

n - коэффициент Пуассона, qn - удельная погонная нормальная нагрузка, [s]HE - допускаемые контактные напряжения с учётом фактических условий работы.

Расчёт зубьев на контактную выносливость для закрытых передач (длительно работают на постоянных режимах без перегрузок) выполняют как проектировочный. В расчёте задаются передаточным отношением, которое зависит от делительных диаметров и определяют межосевое расстояние Аw (или модуль m), а через него и все геометрические параметры зубьев. Для открытых передач контактные дефекты не характерны и этот расчёт выполняют, как проверочный, вычисляя контактные напряжения и сравнивая их с допускаемыми.

 

Расчёт зубьев на изгиб

 

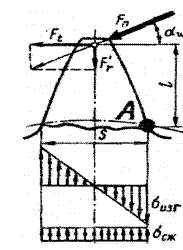Зуб представляют как консольную балку переменного сечения, нагруженную окружной и радиальной силами (изгибом от осевой силы пренебрегают). При этом окружная сила стремится изогнуть зуб, вызывая максимальные напряжения изгиба в опасном корневом сечении, а радиальная сила сжимает зуб, немного облегчая его напряжённое состояние.

sA = sизг А - sсжатия А.

Напряжения сжатия вычитаются из напряжений изгиба. Учитывая, что напряжения изгиба в консольной балке равны частному от деления изгибающего момента Mизг на момент сопротивления корневого сечения зуба W, а напряжения сжатия это сила Fr, делённая на площадь корневого сечения зуба, получаем:

.

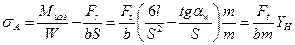Здесь b – ширина зуба, m – модуль зацепления, YH – коэффициент прочности зуба.

Иногда используют понятие коэффициента формы зуба YFH = 1 / YH.

Таким образом, получаем в окончательном виде условие прочности зуба на изгиб : sA = qn YH / m≤ [s]FE .Полученное уравнение решают, задавшись свойствами выбранного материала.

Допускаемые напряжения на изгиб (индекс F) и контактные (индекс H) зависят от свойств материала, направления приложенной нагрузки и числа циклов наработки передачи [s]FE = [s]F KF KFC / SF; [s]HE = [s]H KH / SH.

Здесь [s]F и [s]H – соответственно пределы изгибной и контактной выносливости; SF и SH – коэффициенты безопасности, зависящие от термообработки материалов; KFC учитывает влияние двухстороннего приложения нагрузки для реверсивных передач; KF и KH - коэффициенты долговечности, зависящие от соотношения фактического и базового числа циклов наработки. Фактическое число циклов наработки находится произведением частоты вращения колеса и срока его службы в минутах. Базовые числа циклов напряжений зависят от материала и термообработки зубьев.

Пример расчёта зубьев на контактную выносливость и на изгиб детально изложен в учебном пособии нашей кафедры [3].

Расчёт зубьев на изгиб для открытых передач (работают на неравномерных режимах с перегрузками) выполняют, как проектировочный. В расчёте задаются прочностными характеристиками материала и определяют модуль m, а через него и все геометрические параметры зубьев. Для закрытых передач излом зуба не характерен и этот расчёт выполняют, как проверочный, сравнивая изгибные напряжения с допускаемыми [42].

 

ПЛАНЕТАРНЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ

Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями [8,29]. Эти подвижные колёса подобно планетам Солнечной системы вращаются вокруг своих осей и одновременно перемещаются вместе с осями, совершая плоское движение, называются они сателлитами (лат. satellitum – спутник). Подвижные колёса катятся по центральным колёсам (их иногда называют солнечными колёсами), имея с ними внешнее, а с корончатым колесом внутреннее зацепление. Оси сателлитов закреплены в водиле и вращаются вместе с ним вокруг центральной оси.

Планетарные передачи имеют ряд преимуществ перед обычными:

+ большие передаточные отношения при малых габаритах и массе;

+ возможность сложения или разложения механической мощности;

+ лёгкое управление и регулирование скорости;

+ малый шум вследствие замыкания сил в механизме.

В планетарных передачах широко применяют внутреннее зубчатое зацепление с углом aw = 30о.

Для обеспечения сборки планетарных передач необходимо соблюдать условие соосности (совпадение геометрических центров колёс); условие сборки (сумма зубьев центральных колёс кратна числу сателлитов) и соседства (вершины зубьев сателлитов не соприкасаются друг с другом).

Зубчатые колёса планетарных передач рассчитываются по тем же законам, что и колёса обычных цилиндрических передач [39].