Вирази (3.4), (3.5) є тотожними, якщо

(3.6)

При цьому модуль комплексної амплітуди 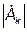буде дорівнювати амплітуді відповідної гармонічної складової, а аргумент — початковій фазі гармонічної складової, тобто

.

Комплексна амплітуда визначається за допомогою формули

.

(3.7)

 

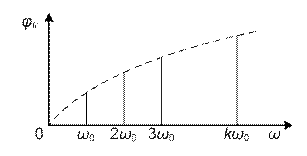
Сукупність амплітуд і частот відповідних гармонічних складових сигналу прийнято називати спектром амплітуд, сукупність початкових фаз і частот відповідних гармонічних складових — спектром фаз, Спектр амплітуд і спектр фаз однозначно визначають сигнал. На
рис. 3.5, б, в подано графічні зображення спектра амплітуд і спектра фаз періодичного сигналу.

Окремі спектральні складові називають спектральними лініями. Особливістю спектра періодичного сигналу є його дискретність. Відстань між сусідніми лініями спектра є однаковою і дорівнює частоті основної гармонічної складової w₀.

 

а

б в

Рис. 3.5. Частотне подання (зображення) періодичного сигналу

Приклад 3.1. Визначити спектр амплітуд періодичної послідовності прямокутних імпульсів тривалістю 2t, амплітудою А з періодом проходження Т (рис. 3.6, а).

Розв’язання. Функцію x(t) (рис. 3.6, а) можна зобразити у вигляді

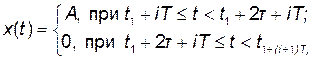i = 0, 1, 2, ..., .

а згідно з (3.5) — рядом Фур’є:

,

 

де .

 

Якщо t₁ = – t, то

 

.

а б

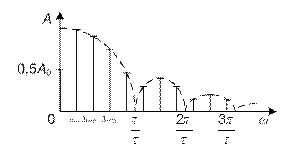
Рис. 3.6. Сигнал і його спектр амплітуд

Відомо, що , а Тw₀ = 2p. Тоді

З урахуванням значень А₀ і А_к розкладення в ряд Фур’є періодичної послідовності прямокутних імпульсів зображується у вигляді

.

(3.8)

З цього виразу випливає, що при А_k = 0. Спектр амплітуд для цього сигналу показано на рис. 3.6, б, а його обвідна визначається виразом

,

де .

З виразу (3.8) випливає, що при збільшенні частоти на величину фаза гармонічних складових змінюється на π. Для розв¢язання багатьох практичних задач (визначення практичної ширини спектра, визначення середньої потужності сигналу та ін.) достатньо обмежитися визначенням тільки спектра амплітуд сигналу.