Основи кодування

 

В СКК КІВ широко використовується передача інформації — кодів. Процес зображення (повідомлень) інформації у вигляді кодів є кодуванням, що є універсальним способом відображення інформації під час зберігання, передавання й оброблення у вигляді системи відповідностей між елементами інформації й сигналами, за допомогою яких ці елементи можна зафіксувати.

Операція відновлення інформації за прийнятим кодом має назву декодування. Внаслідок кодування отримуємо код, внаслідок декодування за кодом — інформацію. Необхідно пам’ятати, що операції (оператори) кодування й декодування взаємозв’язані, утворюють пару (А, А^*) взаємозв’язаних правил (операцій):

.

(2.1)

Під час кодування (виконання правила А) змінюється структура символів (х_і) і не змінюється кількість інформації, яка міститься у початковому зображенні. Це забезпечується за рахунок того, що процеси кодування й декодування взаємно однозначні. Наприклад, якщо елементу х_і з множини Х під час кодування відповідає елемент у_і, то під час декодування елементу у_і відповідає елемент z_i = x_i. Під час кодування потужність множини, яка описує вихідну інформацію (у виразі (2.1) множина Х має потужність N), має бути меншою за потужність множини, яка використовується для кодування (у виразі (2.1) множина Y має потужність N₀ N).

Як множину, яка використовується для кодування, зручно застосовувати числа деякої системи числення. Тоді під час кодування кожному елементу інформації відповідає число, яке має назву коду, або кодової комбінації. Наприклад, елемент вихідної інформації х_і можна закодувати десятковим числом (кодом) [21]₁₀, або двійковим числом (кодом) [10101]₂, або восьмеричним числом (кодом) [25]₈.

Найбільш розповсюдженими є позиційні коди (числа), коли значення символу в коді (числі) визначається його місцем (позицією) в кодовій комбінації. Код (кодова комбінація, число) характеризується перш за все основою й довжиною. У наведеному прикладі для коду [21]₁₀ основа дорівнює 10, довжина — 2; для коду [10101]₂ основа дорівнює 2, довжина — 4; для коду [25]₈ основа дорівнює 8, довжина — 2. Якщо у прийнятій системі кодування коди мають однакову довжину (n = const), то такі коди називають рівномірними, якщо різну
(n ≠ const) — нерівномірними.

Для практичного використання найбільш зручним є рівномірний код з основою 2 — двійковий код. Це обумовлено тим, що його основа легко реалізується технічними засобами (наприклад, одне значення основи — посиленням імпульсу струму або напруги, друге — відсутністю струму або напруги).

Порівняємо системи числення та побудовані на їх основі коди з позицій застосування у СКК КІВ. Загальноприйнятим зараз є позиційний принцип утворення системи числення. У цій системі значення кожного символу (цифри) у числі (коді) залежить від його позиції в ряду символів, які зображують число. Одиниця кожного наступного розряду числа більша за одиницю попереднього в m разів, де m — основа системи числення. Повне число отримаємо, підсумовуючи значення за розрядами:

,

де m — основа системи числення; а_і — значення розрядного коефіцієнта і-го розряду (тобто множник, який приймає значення 0 … m – 1 і показує, скільки одиниць і-го розряду міститься в числі); n — розрядність числа (довжина коду).

Прості числові коди містять кількість елементів, які відповідають кількості розрядів числа N, що виражається цим кодом. Кожний елемент кодової комбінації (коду) може приймати m різних значень. Максимально можлива кількість кодових комбінацій для заданих m і n визначається виразом N_макс = mⁿ.

Чим більша основа системи числення, тим менше розрядів потрібно для зображення даного числа під час передавання та менший час для його передавання. При зображенні чисел технічними засобами реалізується як кожний розряд числа, так і кожне значення основи числа. Тому складність реалізації числа (коду) оцінюють добутком основи m на розрядність (довжину) n:

C = m·n.

(2.2)

Кращою є та реалізація, для якої функція (2.2) набуває мінімального значення. Провівши оптимізацію (2.2) за m, бачимо, що ця функція має мінімум при m = e, тобто коди з двійковою (m = 2) і трійковою (m = 3) основою близькі до оптимальних. Системи з основою 10 та більше істотно менш ефективні. Якщо ж врахувати не тільки складність технічної реалізації чисел (кодів), але й простоту виконання в них арифметичних і логічних операцій, то перевагу потрібно віддати двійковій системі. Елементарні пристрої, які реалізують основу цієї системи, повинні мати всього два стійких стани. Задача розрізнення двох станів, які відповідають двом різним значенням основи, зводиться у цьому випадку до задачі виявлення наявності або відсутності потенціалу або імпульсу струму (напруги), що не викликає труднощів. Логічні й арифметичні операції також найбільш просто виконуються у двійковій системі числення. Тому в інформаційній техніці найширше використовуються двійкова система числення й двійкові коди.

Людина користується десятковою системою числення. Алгоритм перекладу з двійкової системи у звичну для людини десяткову систему є нескладним. Людині важко оперувати з незвичними двійковими числами, та й запис їх на папері виявляється надто громіздким. Тому крім двійкової отримали розповсюдження системи, які, з одного боку, легше зводяться як до двійкової, так і до десяткової системи, а з іншого — дають більш компактний запис. До таких систем належать восьмерична, шістнадцяткова й двійково-десяткова.

Щоб зберегти переваги двійкової системи і зручність десяткової, використовують двійково-десяткові коди. У такій системі кожна цифра десяткового числа записується у вигляді чотирирозрядного двійкового числа (тетради). За допомогою чотирьох розрядів двійкового числа можна утворити 16 різних комбінацій, з яких будь-які десять комбінацій можна зіставити з десятьма значеннями одного розряду десяткового числа (таких варіантів зіставлення буде 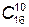= 8008). У двійковій тетраді кожному розряду приписують вагу одиниць (код розряду), а в цілому тетраді приписують код тетради. Цей код означає назву двійково-десяткового коду (наприклад, двійково-десятковий код з вагами 8-4-2-1, або 2-4-2-1, або 5-1-2-1 і т. ін.). Найбільш доцільним з них є код з вагами 8-4-2-1, який широко використовується в СКК КІВ.

Далі при кодуванні будемо в основному використовувати двійкові й двійково-десяткові коди з вагами 8-4-2-1.