Задача 23.

 

Измерительный механизм магнитоэлектрической системы напряжением

U_и =75 мВ с внутренним сопротивлением R_и=10 Ом необходимо использовать для измерения напряжения U_н= 90 B. Найти величину добавочного сопротивления, которое нужно включить последовательно с измерительным механизмом, и ток в вольтметре. Начертить схему включения измерительного механизма с добавочным сопротивлением.

Задача 24.

Измерительный механизм магнитоэлектрической системы рассчитан на ток I_н=15 мА, внутреннее сопротивление прибора R_н=10 Ом. Определить сопроти-вление: а) шунта; б) добавочного сопротивления для измерения этим прибором: тока I_и=9 А; напряжения U_и=36 В. Начертить схему включения измерительного механизма: а) с шунтом; б) с добавочным сопротивлением.

Задача 25.

В однофазную цепь переменного тока с активно – индуктивной нагрузкой включены амперметр, вольтметр, ваттметр. Показания приборов: амперметра – 3,6 А, вольтметра – 180 В, ваттметра – 480 Вт.Определить полное и активное сопротивления, коэффициент мощности цепи. Начертить схему соединений, указать системы применяемых приборов.

Задача 26.

При поверке технического вольтметра, имеющего предел измерения (номинальное напряжение) U_н=150 В и класс точности g_д =1%, была определена его наибольшая абсолютная погрешность _DU=1,8 В. Определить приведенную погрешнось прибора g_п и сделать вывод о соответствии вольтметра ластмасс на нем классу точности.

Задача 27.

Однофазный потребитель подключен к сети с напряжением U=220 В. Актив-ная мощность потребителя P=440 Вт при токе I=2,5 А. Определить коэффици-ент мощности установки cos j и энергию W, израсходованную за 30 часов работы. Начертить схему соединений с приборами для измерения U, I, P и указать системы применяемых приборов.

Задача 28.

Миллиамперметр с пределом измерения (номинальным током) I_н = 250 мА имеет класс точности g_д=1,5%. Определить наибольшую абсолютную погреш-ность миллиамперметра _DI_наиб и наибольшую возможную относительную пог-решность g_нв при измерении тока I = 200 мА этим прибором.

Задача 29.

Ваттметр, включенный для измерения активной мощности однофазного потребителя, имеет следующие номинальные данные: U_н=300 В, I_н=1 А, число делений шкалы a_н=150. При измерении стрелка ваттметра отклонилась на a = 100 делений. Определить показание ваттметра Р и электрическую энергию W, которая израсходована потребителем за t = 12 часов работы.

Задача 30.

Вольтметр с пределом измерения U_н=7,5 В и числом делений a_н=150 имеет наибольшую абсолютную погрешность _DU=36 мВ. Определить класс точности прибора; относительную погрешность для точки a=100 делений.

Задача 31.

В цепь переменного тока включена катушка индуктивности с активным сопротивлением R=8 Ом и индуктивностью L=19,11 мГн. Частота тока 50 Гц. Определить ток в катушке; угол сдвига фаз между током и напряжением; активную, реактивную и полную мощности. Начертить электрическую схему цепи. Построить в масштабе векторную диаграмму тока и напряжений. Построение диаграммы пояснить. Напряжение на зажимах цепи 120 В.

Задача 32.

Неразветвленная цепь переменного тока состоит из активного R=4 Ом и ре-активного X_L=3 Ом сопротивлений. Активная мощность цепи Р=375 Вт.

Определить: полное сопротивление цепи; ток в цепи; напряжение, приложен-ное к цепи; реактивную и полную мощности цепи. Начертить электрическую схему цепи. Построить в масштабе векторную диаграмму тока и напряжений. Построение диаграммы пояснить.

Задача 33.

К неразветвленной цепи переменного тока приложено напряжение U=90 В. Активные сопротивления цепи R₁=8 Ом и R₂=4 Ом, реактивные X_L1=6 Ом и X_L2=10 Ом. Определить: полное сопротивление цепи; ток цепи; активную, реактивную и полную мощности цепи. Начертить электрическую схему цепи. Построить в масштабе векторную диаграмму тока и напряжений. Построение диаграммы пояснить.

Задача 34.

Для неразветвленной цепи переменного тока с активным R=80 Ом, индуктив-ным X_L=75 Ом и ёмкостным X_C=15 Ом сопротивлениями задано напряжение цепи 220 В. Начертить схему цепи. Определить: полное сопротивление цепи; ток в цепи; активную, реактивную и полную мощности цепи; сдвиз фаз между током и напряжением. Построить в масштабе векторную диаграмму тока и напряжений. Построение диаграммы пояснить.

Задача 35.

В неразветвленной цепи переменного тока сопротивления: активное R=80 Ом и ёмкостное X_C=60 Ом, сила тока 6 А. Определить: полное сопротивление цепи; напряжение, приложенное к цепи; сдвиг фаз между током и напряжением; акти-вную, реактивную и полную мощности цепи. Начертить схему цепи. Построить в масштабе векторную диаграмму тока и напряжений. Построение диаграммы пояснить.

Задача 36.

В сеть переменного тока напряжением U=80 В включены параллельно катушка, параметры которой R₁=12 Ом, X_L1=6 Ом и батарея конденсаторов, емкостное сопротивление которой X_C2=22 Ом. Определить токи в паралелльных ветвях I₁, I₂ и ток I в неразветвленной части цепи. Начертить схему цепи. Построить в масштабе векторную диаграмму напряжения и токов, пояснить ее построение.

Задача 37.

В сеть переменного тока напряжением U=120 В включены параллельно кон-денсатор и реостат с активным сопротивлением R₁=12 Ом. Ток в конденсаторе I₂=6 А. Определить ток в реостате I₁; ток в неразветвленной части цепи I; активную Р, реактивную Q и полную S мощности, потребляемаые цепью. Начертить электрическую схему цепи. Построить в масштабе векторную диаграмму токов и напряжения, пояснить ее построение.

Задача 38.

Цепь переменного тока содержит активные сопротивления R₁=32 Ом; R₂=24 Ом и емкостные X_C1=24 Ом; X_C2=32 Ом, образующие две паралелльные ветви. Ток во второй ветви I₂=2 А. Определить ток в первой ветви I₁; ток I в неразветвленной части цепи; напряжение U, приложенное к цепи; активную Р, реактивную Q и полную S мощности, потребляемые цепью. Начертить схему цепи. Построить в масштабе векторную диаграмму напряжения и токов, пояснить ее построение.

Задача 39.

Цепь переменного тока содержит индуктивное X_L1=10 Ом и емкостное X_C2= 20 Ом сопротивления, образующие две параллельные ветви. Напряжение, приложенное к цепи, U=100 В. Определить токи в обеих параллельных ветвях I₁ и I₂, а также ток I в неразветвленной части цепи; активную Р, реактивную Q и полную S мощности, потребляемые цепью. Начертить схему цепи. Построить в масштабе векторную диаграмму напряжения и токов, пояснить ее построение.

Задача 40.

Цепь переменного тока содержит активные R₁=12 Ом, R₂=20 Ом, и индуктив-ное X_L2=15 Ом; емкосное X_C1=16 Ом сопротивления, образующие две паралле-льные ветви. Напряжение, приложенное к цепи, U=200 В. Определить токи в обеих параллельных ветвях I₁ и I₂, а также ток I в неразветвленной части цепи; активную Р, реактивную Q и полную S мощности, потребляемые цепью. Начертить схему цепи. Построить в масштабе векторную диаграмму напряжения и токов, пояснить ее построение

Задача 41.

В четырехпроводную сеть трехфазного тока с линейным напряжением U_л = 380 B включены по схеме «звезда» лампы одинаковой мощности Р₁=200 Вт, число ламп в фазах n_A=10; n_B=20; n_C=15. Вычислить активную мощность, потребляемую цепью; фазные напряжения и токи. Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов. Пояснить ее построение. Определить по векторной диаграмме ток в нулевом проводе I_o.

Задача 42.

В трехфазную сеть с линейным напряжением U_л=220 В включены треу-гольником три разные группы ламп. Мощность ламп в фазах составляет:

Р_AB= 4,4 кВт; Р_BC=2,2 кВт; Р_CA=3,3 кВт. Начертить схему цепи. Определить фазное напряжение; фазные токи I_AB, I_BC, I_CA и мощность Р, потребляемую всеми лампами. Построить в масштабе векторную диаграмму токов и напряжений; найти по векторной диаграмме значения токов в линейных проводах.

Задача 43.

В трехфазную сеть напряжением U_л=380 В включен двигатель. Обмотка двигателя соединена треугольником. Полное сопротивление каждой фазы обмотки двигателя Z_ф=30 Ом; коэффициент мощности двигателя h=0,84. Начертить схему цепи. Вычислить активную мощность двигателя Р; фазное напряжение U_ф; фазный I_ф и линейный I_л токи, активное Р_ф и индуктивное X_Lф сопротивления фазы. Построить в масштабе векторную диаграмму токов и напряжений.

Задача 44.

В трехпроводную сеть трехфазного тока с линейным напряжением U_л=380 В включены по схеме «треугольник» лампы одинаковой мощности Р₁=120 Вт. Число ламп в фазах n_AB=12; n_BC=18; n_CA=24. Вычислить фазные токи и активную мощность, потребляемую цепью. Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов. Пояснить ее построение. Определить по векторной диаграмме линейные токи I_A, I_B, I_C.

Задача 45.

В трехфазную сеть напряжением U_л=380 В включен звездой приемник энер-гии мощностью Р = 6 кВт с коэффициентом мощности двигателя cos j = 0,85.

Начертить схему цепи. Определить фазное напряжение U_ф; фазный I_ф и ли-нейный I_л токи, полное сопротивление фазы Z_ф; полную S и реактивную Q мощности трехфазного потребителя. Построить в масштабе векторную диаг-рамму напряжений и токов.

Задача 46.

В трехфазную сеть напряжением U_л=220 В включен двигатель, потребляю-щий мощность Р = 9 кВт. Обмотки двигателя соединены звездой. Линейный ток двигателя I_л =50 А. Начертить схему цепи. Определить фазное напряжение U_ф, полное Z_ф, активное R_ф и индуктивное X_Lф сопротивление фазы; коэффициент мощности cos j; полную S и реактивную Q мощности двигателя. Построить в масштабе векторную диаграмму напряжений и токов.

Задача 47.

В четырехпроводную сеть трехфазного тока с линейным напряжением U_л = 380 В включены по схеме «звезда» лампы одинаковой мощности. Ток каждой лампы I₁=0,79 А. Число ламп в фазах n_AB=12, n_BC=8, n_CA=15. Вычислить мощность лампы; мощность, потребляемую цепью; фазные напряжения и токи.

Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов. Пояснить ее построение. Определить по векторной диаграмме ток в нулевом проводе I_о.

Задача 48.

В трехпроводную сеть трехфазного тока с линейным напряжением U_л=220 В включены по схеме «треугольник» лампы одинаковой мощности, Р_л = 150 Вт.

Мощности фаз P_AB=3,75 кВт, P_BC=4,5 кВт, P_CA=6,0 кВт. Определить число ламп в фазах, общую мощность потребителя, фазные токи. Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов. Пояснить ее построение. Определить по векторной диаграмме линейные токи I_A, I_B, I_C.

Задача 49.

В трехфазную четырехпроводную сеть напряжением U_л=380В включены при-емники энергии по схеме «звезда». Мощность приемников в фазах: Р_А=1,5 кВт, Р_B=2 кВт, Р_C=1 кВт. Для всех приемников cos j=1. Начертить схему цепи. Оп-ределить фазное напряжение U_ф, фазные I_ф и линейные I_л токи, активную мощ-ность трех фаз. Построить в масштабе векторную диаграмму напряжений и то-ков, графически из векторной диаграммы определить ток в нулевом проводе I_о.

Задача 50.

В четырехпроводную сеть трехфазного тока включены по схеме «звезда» лампы одинаковой мощности. Ток одной лампы I₁=0,5 А. Фазные токи I_A=9 А, I_B = 4,5 А, I_C=5,4 А. Фазные напряжения на лампах U_ф=220 В. Вычислите линейное напряжение сети, число ламп в фазах, общую мощность потребителя, мощность одной лампы. Начертить электрическую схему цепи. Построить векторную диаграмму напряжений и токов. Пояснить ее построение. Определить по векторной диаграмме ток в нулевом проводе I_o.

Методические указания к выполнению

контрольной работы № 1.

Задачи 1-10

включают материал темы «Электрические цепи постоянного тока».

Для их решения необходимо знать закон Ома для всей цепи и для участка, первый закон Кирхгофа, методику определения эквивалентного сопротивления

цепи при смешанном соединении резисторов, а также уметь вычислить мощ-

ность электрического тока.

Методику и последовательность действий при решении задач 1-10 рассмотрим на конкретном примере.

Пример 1.

Определить эквивалентное сопротивление цепи, схема которой представлена на рис., если заданы значения сопротивлений резисторов R₁=8 Ом, R₂=4 Ом, R₃=2 Ом, R₄=4 Ом, R₅= 4 Ом. Напряжение сети U=16 В. Вычислить токи, проходящие через каждый резистор, и мощность, потребляемые цепью.

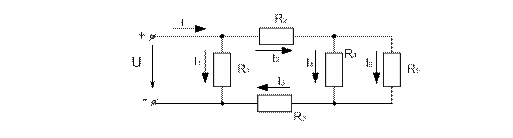
1. Делаем краткую запись условия задачи:

Дано: R₁=8 Ом, R₂=4 Ом, R₃=2 Ом, R₄=4 Ом, R₅=16 В.

Определить: R_экв,I₁, I₂, I₃,I₄, I₅, P.

Решение.

2. Обозначим стрелками токи, проходящие через каждый резистор с учетом их направления.

3. Определим общее (эквивалентное) сопротивление цепи, метод подсчета кото-рого для цепи со смешанным соединением резисторов сводится к последова-тельному упрощению схемы:

- сопротивления R₄ и R₅ соединены параллельно. Найдем общее сопротивле-ние при таком соединении: R_4,5 = R₄×R₅/(R₄+R₅) = 4×4/(4+4) = 2 Ом;

- резисторы R₂, R₃, R_4,5 соединены последовательно. Их общее сопротивле-ние: R_2-5= R_2,3,4,5= R₂+R₃+R_4,5 = 4+2+2 = 8 Ом;

- сопротивления R₁ и R_2-5 соединены параллельно. Эквивалентное сопротив-ление цепи: R_экв= R₁×R_2-5/(R₁+R_2-5) = 8×8/(8+8) = 4 Ом.

4. Общий ток по закону Ома для участка цепи: I = U/R_экв = 16/4 = 4 A.

5. Токи, проходящие через сопротивление цепи:

- ток в первом сопротивлении: I = U/R₁ = 16/8 = 2 A.

(сопротивление R₁ соединено с зажимами цепи, поэтому напряжение на R₁ равно: U₁=U=16 B. Такое же напряжение будет на сопротивлении R_2-5).

- ток во втором и третьем сопротивлениях: I₂ = I₃ = I – I₁ = 4 – 2 = 2 A.

- чтобы найти токи I₄ и I₅ надо знать U_4,5.

Это напряжение можно найти двумя способами: U_4,5 = I₂×R_4,5=2×2=4 B, или

U_4,5 = U – U₂ – U₃=16 – 2×4 – 2×2=4 B.

По закону Ома для параллельно соединенных сопротивлений:

I₄ = U_4,5/R₄ = 4/4 = 1 A; I₅ = U_4,5/R₅ = 4/4 = 1 A.

Проверка: I₂ = I₄ + I₅; 2 = 1 + 1; 2 A = 2 A.

6. Мощность, потребляемая цепью: P = U×I = 16×4 = 64 Вт.

Задач 11 – 20.

Для их решения надо изучить тему «Электромагнетизм» и хорошо усвоить основные характеристики магнитного поля:

- магнитная индукция – В (Тл). Она определяет интенсивность магнитного по-ля в точке и является основной характеристикой магнитного поля.

- магнитная проницаемость: m - характеризует магнитные свойства среды по сравнению с вакуумом; m=m_а/m_о – относительная магнитная проницаемость, величина безразмерная; m_о - магнитная постоянная, равная 4×p×10^-7 Гн/м;

- магнитный поток – Ф (Вб).

- напряженность магнитного поля – Н (А/м). Она является вспомогательной расчетной величиной.

В=m_а×Н – формула зависимости магнитной индукции от напряженности магнитного поля через абсолютную магнитную проницаемость.

Для немагнитных сред (воздух) относительная магнитная проницаемость близка к единице. Такие среды предусмотрены в условиях задач. Тогда абсолютная магнитная проницаемость: m_а = m_о×m = 4×p×10^-7 Гн/м. (m =1)

Для ферромагнитных материалов, которые используются для изготовления частей электрических машин аппаратов, приборов, величина относительной магнитной проницаемости велика и составляет тысячи, десятки, сотни тысяч единиц.

Пример 2.

Кольцевая катушка намотана на каркасе из немагнитного материала (рис. 13). Внутренний радиус катушки R₁=1,5 см, внешний R₂=2,5 см. Напряженность магнит-ного поля по средней магнитной линии катушки Н=3600 А/м; ток в лтушке I=10 А. Определить число витков катушки w и магнитную индукцию В по cредней линии катушки.

Решение.

1. Индукция магнитного поля по средней линии катушки:

B = m×m_o×H =1×4×p×10^-7×3600=4,52×10^-3 Тл, где m_o – магнитная постоянная;

m=1 – oтносительная магнитная проницаемость немагнитного материала сердечника катушки.

2. Число витков катушки найдем из формулы напряженности магнитного поля по средней магнитной линии: H=I×w/2×p×R_ср, где R_ср=(R₁+R₂)/2=2 см=2×10^{-2 м;}

w=2×p×R_ср×H/I = 2×3,14×2×10^-2×3600/10=45 витков.

Пример 3.

По проводу длиной ℓ=0,8 м, находящемуся в магнитном поле с индукцией

В=1,25 Тл, проходит ток, поступающий от источника энергии с напряжением U=4 В. Под действием электромагнитной силы провод будет перемещаться по направляющим со скоростью υ = 2,5 м/с. Линии магнитного поля показаны на рисунке точками и направлены из-за плоскости чертежа к наблюдателю. Соп-ротивление провода R_o=0,2 Ом. Определить индуктированную ЭДС – Е; электромагнитную силу F и ток I в проводе при движении его в магнитном поле. Направление ЭДС, силы и тока показаны на рисунке.

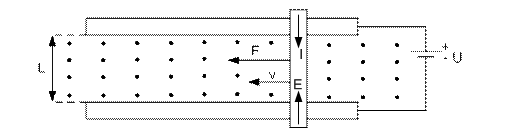
Решение.

1. Ток проходит от положительного полюса источника (+) к отрицательному (-).Под действием электромагнитной силы проводник будет перемещаться вле-во (правило левой руки); направление силы F и скорости υ одинаково. В прово-днике будет наводиться ЭДС (явление электромагнитной индукции), равная:

E = B×ℓ×υ = 1,25×0,8×2,5 = 2,5 B.

Направление ЭДС определим по правилу правой руки. Оно противоположно направлению ЭДС внешнего источника и тока, поэтому эта ЭДС (в электродви-гателях) называется противо-ЭДС.

2. Ток в проводнике: I = (U – E)/Ro = (4 – 2,5)/0,2 = 7,5 A.

3. Электромагнитная сила, под действием которой перемещается проводник:

F = B×I×ℓ=1,25×7,5×0,8=7,5 H.

Для решения задачи 14 необходимо знать, что подъемной силой электромаг-нита называется наименьшая сила, при которой подвижная часть электромагни-та может быть оторвана от неподвижной.

Для подсчета подъемной силы электромагнита используется формула:

F = 4×10⁵×B²×S, где S – суммарная площадь сечения полюсов, м²;

В – магнитная индукция, Тл.

Для решения задач 16, 19 надо помнить, что длинную и узкую цилиндричес-кую катушку можно считать частью кольцевой катушки с достаточно большим радиусом. Поэтому при расчете таких катушек следует применять формулы для кольцевых катушек.

1. Магнитный поток Ф (Вб) сквозь поперечное сечение катушки: Ф=m_a×I×w×S/ℓ, где m_a- абсолютная магнитная проницаемость, w –число витков катушки, I – ток катушки, ℓ-длина катушки, S – площадь сечения катушки: S=p×d²/4 (м²).

2. Индуктивность катушки – L(Гн): L = m_a×w²×S/ℓ .

При включении и выключении цепи ток изменяется по значению, что сопро-вождается изменением магнитного потока, который, пересекая витки катушки, наводит в них ЭДС, называемую ЭДС самоиндукции – e_L. Ее величину опреде-ляют по формуле: e_L= - L×di/dt , где L – индуктивность катушки, Гн; di/dt - скорость изменения тока (А/c); e_L - ЭДС самоиндукции (В).

Задачи 21 – 30.

Посвящены теме «Электрические измерения». Надо помнить, что результат измерения всегда отличается от действительного значения измеряемой величиныны. Разность между показаниями приборов и действительным значением измеряемой величины называют абсолютной погрешностью: _DA = A_и – A_д, где

A_и – показания прибора, А_д – действительное значение измеряемой величины (под А подразумевают напряжение, ток и другие измеряемые величины).

Отношение абсолютной погрешности к действительному значению измеряе-мой величины (или показанию прибора) называют относительной погрешнос-тью измерения: g = _DА/А_д×100% (т.к. А_д и А_и мало отличаются).

Важнейшей характеристикой измерительного прибора является класс точнос-ти, который указывается на приборе. Каждый класс характеризуется наиболь-шей относительной допустимой приведенной погрешностью, величина которой равна номеру класса и определяется по следующей формуле: g_д=_DА_наиб/А_н×100%,

где А_н – верхний предел измерения прибора; _DА_наиб – наибольшая разность меж-ду показаниями прибора и действительным значением измеряемой величины А. По классу точности прибора можно подсчитать наибольшую абсолютную погр-ешность, которую может иметь прибор в любой точке шкалы: _DА_наиб = g×А_н×100

Точность измерения характеризуется также наибольшей возможной относи-тельной погрешностью: g_{н в}=_DА_наиб/А_и×100% или g_{н в} = g_д×А_н/А_и.

Для расширения пределов измерения измерительных механизмов (ИМ) маг-нитоэлектрической системы по току используют шунты, которые включают па-раллельно измерительному механизму. Для расширения пределов измерения

ИМ по напряжению в цепях постоянного тока и в цепях переменного тока нап-ряжением до 600 В применяются добавочные резисторы, которые включают последовательно с измерительным механизмом.

Пример 4.

При проверке технического вольтметра электромагнитной системы типа Э378, имеющего предел измерения 250 В, была определена его наибольшая абсолютная погрешность _DU_наиб=3,75 В.

Определите класс точности вольтметра g_д, наибольшую возможную относите-льную погрешность измерения g_{н в1} и g_{н в2} для показаний вольтметра U₁=100 B и U₂= 200 В.

Решение.

1. Класс точности вольтметра: g_д = _DU_наиб/U_н ×100% = 3,75/250×100% = 1,5%.

2. Наибольшие возможные относительные погрешности измерения, если во-льтметр показал: U₁ = 100 B g = _DU_наиб/U₁×100% = 3,75/100×100% = 3,75%;

U₂ = 200 B g = _DU_наиб/U₂×100% = 3,75/200×100% = 1,875%.

Пример 5.

Измерительный механизм магнитоэлектрической системы рассчитан на ток I_н=20 мА и имеет шкалу на a_н=100 делений. Сопротивление ИМ R_н=10 Ом.

Определить сопротивление шунта и постоянную (цену деления) амперметра, если этим прибором нужно измерить ток I_и=30 А. Определить величину сопро-тивления добавочного резистора и постоянную (цену деления) вольтметра, если этим прибором нужно измерить напряжения U_и=75 В.

Решение.

1. Шунтирующий множитель: n = I_и/I_н = 30/20×10^-3 = 1500.

2. Сопротивление шунта: R_ш = R_н/(n -1) = 10/(1500 – 1) = 0,0067 Ом.

3. Постоянная (цена деления) амперметра: С_I = I_и/a_н = 30/100 = 0,3 А/дел.

4. Падение напряжения на измерительном механизме:

U_н= I_н×R_н =20×10^-3×10 =200×10^-3 В =200 мВ.

5. Множитель добавочного резистора: m = U_и/U_н = 75/200×10^-3 = 375.

6. Сопротивление добавочного резистора: R_д =R_н×(m -1)=10×(375 –1)=3740 Ом.

7. Постоянная (цена деления) вольтметра: С_U = U_и/a_н = 75/100 = 0,75 В/дел.

На рис. а представлена схема включения в цепь измерительного механизма с шунтом, на рис. б – измерительного механизма с добавочным резистором.

Задачи 31- 40 посвящены расчету однофазного переменного тока.

При изучении материала темы «Однофазные электрические цепи переменного тока» надо усвоить основные величины, характеризующие синусоидальные токи и напряжения: амплитуда, частота, начальная фаза, сдвиг фаз между током и напряжением, мгновенное и действующее значение. Надо научиться строить векторные диаграммы токов и напряжения сначала для цепи только с активным сопротивлением, а затем только с индуктивным или только с емкостным сопротивлением, а затем для неразветвленной и разветвленной цепи, содержащей все три вида сопротивлений.

В неразветвленной (последовательной) цепи переменного тока приложенное

напряжение определяется как геометрическая сумма активной и реактивной составляющих напряжения.

Для неразветвленной цепи строится векторная диаграмма напряжений и тока, причем за исходный вектор берется вектор тока, так как ток будет одинаковым во всех участках цепи.

Надо усвоить, что напряжение на активном сопротивлении совпадает с током по фазе, напряжение на индуктивности опережает ток по фазе на угол 90^о, нап-ряжение на емкости отстает от тока на 90^о.

В разветвленной (параллельной) цепи общий ток, то есть ток в неразветвлен-ном участке цепи, определяется как геометрическая сумма активной и реактив-ной составляющих тока. Сами параллельные ветви рассчитываются как нераз-ветвленные цепи переменного тока. Для разветвленных цепей строится вектор-ная диаграмма токов и напряжения, так как на всех параллельных ветвях напря-жение одинаковое.

Пример 6.

Сопротивления катушки: активное R_к=4 Ом, индуктивное X_L=12 Ом. Последовательно с катушкой включен резистор с активным сопротивлением R=2 Ом и конденсатор с сопротивлением X_C= 4 Ом. К цепи приложено напряжение U = 100 В. Определить полное сопротивление цепи, силу тока, коэффициент мощности, активную, реактивную и полную мощности; напряжение на каждом сопротивлении. Начертить в масштабе векторную диаграмму цепи.

Решение.

1. Полное сопротивление цепи:Z=Ö(R_к+R)² +(X_L–X_C)² =Ö(4+2)² +(12–4)² =10 Ом.

2. Сила тока в цепи: I = U/Z = 100/10 = 10 A.

3. Коэффициент мощности в цепи: cos j = (R_к +R)/Z = (4 +2)/10 = 0,6.

По таблицам Брaдиса находим j = 53^o10¢.

4. Активная мощность цепи: P = I²×(R_к + R) = 10²×(4 + 2) = 600 Вт

или P = U×I×cos j = 100×10×0,6 = 600 Вт.

5. Реактивная мощность цепи: Q = I²×(X_L – X_C) = 10²×(12 – 4) = 800 Вар или Q = U×I×sin j = 100×10×0,8 = 800 Вар; sin j = (X_L – X_C)/Z = (12 – 4)/10 = 0,8.

6. Полная мощность цепи: S = U×I = ÖP² +Q² = Ö600² +800² = 1000 BA.

7. Напряжения на сопротивлениях цепи: U_к = I×R_к = 10×4 = 40 B;

U_R = I×R = 10×2 =20 B; U_L = I×X_L = 10×12 = 120 B; U_C = I×X_C = 10×4 = 40 B.

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаем масштабы по току: М_I =2,5 А/см и по напряжению:

М_U = 20 В/см.

Построение векторной диаграммы начинаем с вектора тока, длина которого

ℓ = I/M_I = 10 A/2,5 A/см = 4 см откладывается по горизонтали.

Вдоль вектора тока откладываем векторы напряжений на активных сопротив-лениях U_к и U_R, длины которых равны: ℓ_Urк = U_Rк/M_U = 20/20 = 1 см;

ℓ_UR = U_R/M_U = 40/20 = 2 см.

Из конца вектора`U<sub>R</sub> откладываем в сторону опережения вектора тока на 90° вектор напряжения`U_L на индуктивном сопротивлении длиной:

ℓ_UL= U_L/M_U = =120/20 = 6 см.

Из конца вектора`U<sub>L</sub> откладываем в сторону отставания от вектора тока на 90° вектор напряжения на конденсаторе`U_C длиной: ℓ_UC = U_C/M_U = 40/20 = 2 см.

Геометрическая сумма векторов`U<sub>к</sub>,`U_R,`U<sub>L</sub>,`U_C равна напряжению`U, приложенному к цепи.

Пример 7.

Катушка с активным сопротивлением R=8 Ом и индуктивным X_L1=6 Ом сое-динена параллельно с конденсатором, емкостное сопротивление которого равно X_C2=20 Ом. Определить: токи в ветвях и в неразветвленной части цепи, активные и реактивные мощности ветвей и всей цепи, полную мощность всей цепи, углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи. Начертить в масштабе векторную диаграмму цепи. К цепи приложено напряжение U=60 В.

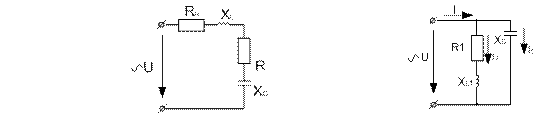
Решение.

1. Токи в каждой ветви: I₁=U/Z₁; I₂=U/Z₂, где Z₁=ÖR₁² +X_L1² = Ö8² +6² =10 Ом;

и Z₂ = X_C2 = 20 Ом – полные сопротивления ветвей.

Тогда I₁=60/10=6 A; I₂ = 60/20 3 A.

2. Углы сдвига фаз в ветвях находим по синусам углов во избежание потери знака угла:

sin j₁=X_L1/Z₁=6/10=0,6 j₁=36°50¢, напряжение опережает ток, так как j₁ > 0;

sin j₂ =-X_C2/Z₂= -20/20= -1; j₂= -90°, напряжение отстает от тока, так как j₂ < 0.

По таблицам Брадиса находим: cos j₁ = cos 36°50¢ = 0,8; cos j₂ = 0.

3. Активные и реактивные составляющие токов ветвей:

I_a1=I₁×cos j₁=6×0,8=4,8 A; I_p1=I₁×sin j₁=6×0,6=3,6 A; I_a2=0; I_p2=3×(-1) = -3 A.

4. Ток в неразветвлённой части цепи:

I=Ö(I_a1+I_a2)²+(I_p1+I_p2)² = Ö(4,8 + 0)²+(3,6 – 3) = 4,83 A.

5. Коэффициент мощности всей цепи: cos j = (I_a1 + I_a2)/I = 4,8/4,83 = 0,992.

6. Активные и реактивные мощности ветвей и всей цепи:

P₁ = I₁²×R₁ = 6×28 = 288 Вт; P₂=0; P = P₁ + P₂ = 288 Вт.

Q₁ = Q_L = I₁²×X_L1 = 6²×6 = 216 ВАр; Q₂ =Q_C = I₂²×X_C2 = 3²×20 =180 ВАр;

Q = Q₁ +Q₂ = 216 – 180 = 36 Вар.

(реактивная мощность ветви с емкостью Q₂–отрицательна, т. к. угол j₂ < 0).

7. Полная мощность цепи: S = ÖP² +Q² = Ö288² + 36² = 296 BA.

8. Ток в неразветвленной части цепи можно определить и без разложения токов

ветвей на составляющие: I = S/U = 296/60 = 4,83 A.

Для построения векторной диаграммы задаем масштабы по току М_I=1 А/см

и по напряжению М_U=10 В/см. Построение начинаем с вектора напряжения.

Под углом j₁ к нему (в сторону отставания) откладываем в масштабе вектор тока `I<sub>1</sub>; под углом j<sub>2</sub> (в сторону опережения) – вектор тока`I₂. Геометрическая сумма этих токов равна току`I в неразветвленной части цепи. На диаграмме показаны также проекции векторов токов на вектор напряжения (активная составляющая I_a1) и вектор, перпендикулярный ему (реактивные составляющие I_p1 и I_p2)

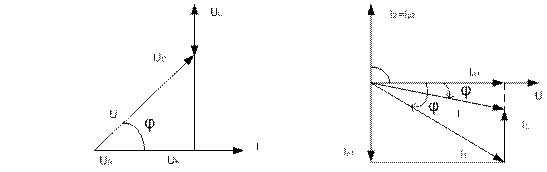
Задачи 41-50 посвящены теме «Трехфазные электрические цепи».

В трехфазных системах потребители соединяются по схеме звезда» или «треугольник».

При соединении приемников энергии «звездой» линейные напряжения об-означаются U_л, U_AB, U_BC, U_CA; фазные напряжения обозначаются: U_ф,U_A,U_B,U_C;

токи – I_A, I_B, I_C, причем токи линейные равны соответствующим фазным токам: I_л = I_ф. При наличии нейтрального провода при любой нагрузке, а при равно-мерной нагрузке и без нейтрального провода: U_л = Ö3×U_ф.

При соединении потребителей энергии «треугольником» фазное напряжение равно линейному: U_ф = U_л. Обозначаются напряжения: U_AB, U_BC, U_CA, фазные токи обозначаются: I_ф, I_AB, I_BC, I_CA. Линейные токи обозначаются: I_л, I_A, I_B, I_C. При неравномерной нагрузке фаз линейные токи определяются из векторной диаграммы, как геометрическая разность фазных токов.

При соединении приемников энергии «звездой» сеть может быть четырехпро-водной – при наличии нейтрального провода или трехпроводной – без нейтра-льного провода. При соединении «треугольником» - только трехпроводной.

Пример 8.

Осветительные лампы трех этажей станции соединены «звездой» и присоеди-нены к трехфазной четырехпроводной линии с напряжением U_л= 380 В.

проводе.

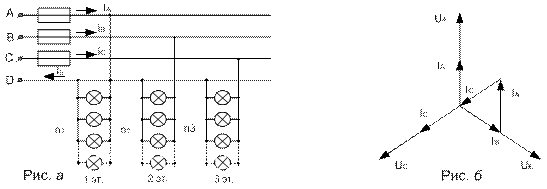
Число ламп на каждом этаже одинаковое n₁ = n₂ = n₃ = 50. Мощность каждой лампыP₁ =100 Вт. Определить: фазные токи I_A, I_B, I_C при одновременном включении всех ламп на каждом этаже; фазные активные P_A, P_B, P_C мощности и мощность Р всей трехфазной цепи. Вопрос: чему будет равен ток в нейтралном проводе?

Решение.

1. Определяем фазные мощности, исходя из того, что в каждой фазе включено по 50 ламп мощностью Р₁ каждая: P_A = P_B = P_C = n×P₁ = 50×100 =5000 Вт=5 кВт.

Тогда мощность цепи: Р = Р_А + Р_В + Р_С = 3×5 = 15 кВт.

2. Фазные (они же линейные) токи найдем из формулы фазной мощности:

Р_ф = U_ф×I_ф×cos j_ф , предварительно определив фазное напряжение: U_ф = U_л/Ö3 = 380/1,73 = 220 B; cos j_А= cos j_В= cos j_С=1 (нагрузка активная), тогда I_A=I_B =I_C= = P_ф/(U_ф×cos j_ф) = 5000/220×1 = 22,7 A.

3. Для определения тока в нейтральном проводе надо построить векторную диаграмму напряжений и токов. Выбираем масштабы: для напряжений М_U = 50 В/см, для токов М_I = 10 А/см. Длины векторов: ℓ_Uф = U_ф/M_U = 220/50 = 4,4 см; ℓ_IA = ℓ_IB = ℓ_IC = I_ф/M_I = 22,7/10 = 2,27 см.

Порядок построения диаграммы:

1. Из точки 0 проводим три вектора фазных напряжений`U<sub>A</sub>,`U_B,`U_C, углы между которыми составляют 120°.

2. Векторы фазных токов`I<sub>A</sub>,`I_B,`I_C будут иметь одинаковую длину, т.к. значения токов одинаковые. Направлены они вдоль соответствующих векторов фазных напряжений.

3. Геометрически складывая токи I_A, I_B, I_C получаем ток в нейтральном проводе

I_O =`I<sub>A</sub> +`I_B +`I_C.

Из диаграммы видно, что ток в нейтральном поводе I_O равен нулю.

Пример 9.

Трехфазный двигатель мощностью Р=15 к Вт, при cos j=0,87 питается от сети с линейным напряжением U_л=380 В. Обмотки двигателя соединены треуголь-ником. Определить фазное напряжение U_ф, фазный I_ф и линейный I_л токи, пол-

ное сопротивление фазы Z_ф, полную S и реактивную Q мощности двигателя. Построить в масштабе векторную диаграмму напряжений и токов.

Решение.

1. При соединении треугольником (рис. а) фазное напряжение равно линейному, т.е. U_ф = U_л = 380 В.

2. Из формулы активной мощности находим фазный ток двигателя:

I_Ф = P/3×U_ф×cos j = 15×10³/(3×380×0,87) = 15 А.

3. Полное сопротивление фазы по закону Ома: Z_ф= U_ф/I_ф = 380/15 =25 Ом.

4. Линейный ток при равномерной нагрузке фаз: I_л = Ö3×I_ф = Ö3×15 =26 А.

5. Полная мощность двигателя:

S=3×U_ф×I_ф= Р/cos j =15000/0,87 = 17240 ВА= »17,2 кВА.

6. Реактивная мощность двигателя:

Q = 3×U_ф×I_ф×sin j = S×sin j = 172400,5 = 8620 Вар » 8,6 кВАр.

Построение векторной диаграммы.

Задаемся масштабом: по току M_I =5 A/см; по напряжению М_U=100 В/см.

Длина векторов фазных (линейных) напряжений: ℓ_Uф =Uф/M_U =380/100=3,8 см;

Длина векторов фазных токов в масштабе: ℓ_Iф = I_ф/М_I = 15/5 = 3 см.

При построении векторной диаграммы вначале откладываем три вектора фазных (линейных) напряжений со сдвигом относительно друг друга на 120°. Векторы фазных токов отстают от векторов фазных напряжений на угол j = 30°,

(cos j =0,87), т.к. нагрузка активно–индуктивная. Соединив концы векторов фазных токов, получаем треугольник линейных токов; при этом векторы

линейных токов являются разностью векторов соответствующих фазных токов:

I_A =`I<sub>AB</sub> -`I_CA; ` I<sub>B</sub> =`I_BC -`I<sub>AB</sub>; `I_C =`I<sub>CA</sub> -`I_BC.

Векторная диаграмма приведена на рис. б.

Контрольная работа № 2.

Задача 1.

Понижающий однофазный двухобмоточный трансформатор подключен к сети с напряжением U₁=220 В; напряжение вторичной обмотки U₂=22 В. Транcформатор работает в номинальном режиме и используется для питания специальной аппаратуры, имеющей активное сопротивление R=2,2 Ом (рис. 1). Определить токи первичной и вторичной обмоток; коэффициент трансформации трансформатора. Начертить электрическую схему включения трансформатора.

Задача 2.

Трехфазный трансформатор имеет следующие данные: номинальная мощность S=25 кВА, номинальные напряжения обмоток U₁=6 кВ; U₂=0,4 кВ. Максимальный магнитный поток в сердечнике Ф_мах=0,02 Вб; схема соединения обмоток «звезда–звезда» с нулевым выводом. Начертить электрическую схему соединения обмоток трансформатора; определить коэффициент трансформации k; число витков обмоток w₁ и w₂; линейные токи в обмотках I₁ и I₂. Частота тока питающие сети f=50Гц.

Задача 3.

Однофазный трансформатор, номинальная мощность которого S=600 кВА, включен в сеть с напряжением U₁=5 кВ и частотой f=50 Гц. Число витков ларичной обмотки w₂= 32, Максимальный магнитный поток в сердечнике Ф_мах= 0,06 Вб. Определить токи в обмотках трансформатора; напряжение вторичной обмотки U₂; коэффициент трансформации k. Начертить электрическую схему соединений для проведения опыта холостого хода трансформатора.

Задача 4.

Двухобмоточный однофазный трансформатор используется для питания пониженным напряжением осветительной аппаратуры (рис. 2). Первичная обмотка трансформатора подключена к сети с напряжением U₁=220 В. Вторичная обмотка питает лампы накаливания одинаковой мощности. Число витков первичной обмотки w₁=6000; число витков вторичной обмотки w₂=600; ток вторичной обмотки I₂=10А. Определить напряжение вторичной обмотки U₂ трансформатора; коэффициент трансформации k; активную мощность, отдаваемую вторичной обмоткой трансформатора Р₂. Начертить электрическую схему трансформатора.

Задача 5.

Трехфазный трансформатор имеет следующие номинальные данные: номинальная мощность S=160 кВА; напряжение первичной обмотки U₁=10кВ; напряжение вторичной обмотки U₂=0,4кВ; потери мощности в опыте холостого хода ∆Р_ст=0,565 кВт, потери мощности в опыте короткого замыкания ∆Р_кз= 2,65кВт; коэффициент мощности cos φ =0,8; схема соединения обмоток «звезда–звезда» с нулевым выводом. Определить номинальные токи в обмотках; номинальный КПД; коэффициент трансформации и суммарные потери мощности в трансформаторе. Начертить электрическую схему соединения обмоток трансформатора.

Задача 6.

Трехфазный трансформатор, обмотки которого рассчитаны на номинальное напряжение U₁=6 кВ и U₂=0,23 кВ отдает со вторичной обмотки активную мощность Р₂=40 кВт и реактивную Q₂=20 кВАр; номинальный ток вторичной обмотки I₂=158 А. Схема соединения обмоток «звезда-звезда» с нулевым выводом. Определить номинальную мощность трансформатора; коэффициент трансформации k; его коэффициент нагрузки k_н; номинальный ток первичной обмотки и КПД трансформатора при номинальной нагрузке. Начертить электрическую схему соединения обмоток трансформатора.

Задача 7.

Однофазный трансформатор работает в номинальном режиме и имеет следующие характеристики: номинальная мощность S=100 кВА; токи в обмотках I₁=16,7 А; I₂=250 А. Трансформатор работает на нагрузку с cos φ =0,8. В сердечнике создается магнитный поток Ф= 0,017 Вб. Частота тока в сети f=50Гц. Потери в стали составляют ∆Р_ст= 400 Вт, потери в обмотках ∆Р_кз=2000 Вт. Определить: ЭДС в обмотках Е₁ и Е₂; коэффициент трансформации k; число витков обмоток; КПД трансформатора. Начертить электрическую схему включения трансформатора.

Задача 8.

Трехфазный трансформатор имеет номинальные данные: номинальная мощность S = 400 кВА; номинальное напряжение обмоток U₁=6 кВ; U₂=0,4 кВ. Схема соединения обмоток «звезда–звезда» с нулевым проводом. Коэффициент нагрузки его равен k_н=0,8; потери мощности в стали ∆Р_ст=0,9 кВт; потери мощности в обмотках ∆Р_кз=5,5 кВт. Определить коэффициент трансформации k; номинальные токи в обмотках; действительные токи в обмотках при заданном значении k_н; суммарные потери мощности в трансформаторе ∆Р при номинальной нагрузке. Начертить электрическую схему соединения обмоток трансформатора.

Задача 9.

Понижающий однофазный двухобмоточный трансформатор подключен к сети с напряжением U₁=220 В. Трансформатор работает в номинальном режиме и используется для питания стенда, имеющего активно – индуктивную нагрузку (рис.3). Номинальная мощность трансформатора S=220 ВА; напряжение ларичной обмотки U₂=44 В. КПД трансформатора η=0,8; коэффициент мощности вторичной цепи cos φ=0,91. Определить ток вторичной обмотки; коэффициент трансформации k; активную номинальную мощность, потребляемую трансформатором из сети Р₁; активную номинальную мощность Р₂, отдаваемую трансформатором в нагрузку. Начертить электрическую схему включения трансформатора.

Задача 10.

Двухобмоточный однофазный трансформатор используется для питания ламп накаливания. Первичная обмотка трансформатора подключена к сети с напряжением U₁=240 В. К вторичной обмотке подключены лампы одинаковой мощности Рл=12 Вт (мощность одной лампы). Коэффициент трансформации трансформатора k=10; активная мощность, отдаваемая трансформатором Р₂=240 Вт. Определить напряжение вторичной обмотки трансформатора U₂; ток вторичной обмотки трансформатора I₂; ток одной лампы Iл; число ламп n. Начертить электрическую схему включения трансформатора.

Задача 11.

Трехфазный шестиполюсной асинхронный двигатель (2р = 6), включен в сеть с напряжением U₁=380 В, частотой f₁=50 Гц, развивает полезный вращающий момент М₂=41 H·м при скольжении s=5%. Мощность, потребляемая двигателем Р₁=5,2 кВт; ток I₁=11 А. Определить частоту вращения ротора n₂, полезную мощность двигателя P₂, КПД – η и коэффициент мощности cos φ, суммарные потери мощности в двигателе ΣP.

Задача 12.

Трехфазный асинхронный двигатель имеет следующие номинальные характеристики: номинальная мощность Р_н=11 кВт; частота вращения ротора n₂=2900 об/мин; номинальный КПД - η=0,88; коэффициент мощности cos φ =0,9. Номинальное напряжение двигателя U_н= 380 В. Частота тока в сети f_1н=50 Гц. Определить частоту вращения магнитного поля n₁; скольжение s; номинальный момент М_н двигателя.

Задача 13.

На заводе для работы вентиляторов используются асинхронные двигатели. Двигатели подключены к электрической сети с напряжением U_н=380 В. Число полюсов двигателя 2р=6, номинальная мощность Р_2н=55 кВт; скольжение s_н=4,4 %, коэффициент мощности cos φ_н = 0,88; КПД - η_н=0,93; частота тока в сети f_1н=50 Гц. Определить частоту вращения магнитного поля статора n₁; частоту вращения ротора n₂; ток двигателя I₁; номинальный момент вращения М_н; активную мощность, потребляемую двигателем из сети Р_1н.

Задача 14

Трехфазный двухполюсной асинхронный двигатель (2р=2) питается от сети с напряжением U₁=380 В, частотой f₁=50 Гц. Двигатель имеет следующие данные: полезная мощность Р₂=55 кВт; скольжение s=2 %; КПД – η=88 %; коэффициент мощности cos φ =088. Определить ток I₁ и мощность P₁, потребляемые двигателем из сети; частоту вращения магнитного поля статора n₁ и частоту вращения ротора n₂, полезный вращающий момент М₂ и суммарные потери мощности в двигателе ΣP.

Задача 15.

Трехфазные асинхронные двигатели используются для работы токарных станков. Все двигатели работают в номинальном режиме и подключены к сети с линейным напряжением U₁= 380 В, промышленной частоты f=50 Гц. Число полюсов двигателей 2р=8; номинальная мощность Р_2н=15 кВт; частота вращения ротора n_2н=735 об/мин. Коэффициент мощности cos φ_н = 0,91 и КПД – η_н = 0,89. Определить частоту вращения магнитного поля статора n₁; скольжение s_н; ток двигателя I_1н; номинальный момент вращения M_н; активную мощность, потребляемую двигателем из сети P_1н.

Задача 16.

Трехфазный четырехполюсный асинхронный двигатель (2р=4) имеет следующие номинальные данные: номинальная мощность Р₂=115 кВт; напряжение сети U₁= 220В; частота тока в сети f₁=50Гц; коэффициент мощности cos φ =0,99; КПД η=0,91; частота вращения ротора n₂=1455 об/мин. Определить мощность, потребляемую двигателем P₁; ток двигателя I₁; вращающий момент М; номинальное скольжение s.

Задача 17.

Трехфазный восьмиполюсный асинхронный двигатель (2р = 8) включен в сеть напряжением U₁=380 В и частотой f₁=50 Гц. Двигатель развивает вращающий момент M₂=911 н·м при скольжении s=2 %. Потребляемая из сети мощность Р₁=81 кВт, ток I₁=140 А. Определить частоту вращения магнитного поля статора n₁; частоту вращения ротора n₂; коэффициент мощности двигателя cos φ; КПД – η; полезную мощность двигателя P₂и суммарные потери мощности ΣP в нем.

Задача 18.

Трехфазный асинхронный двигатель с короткозамкнутым ротором работает в номинальном режиме и подключен к электрической сети напряжением U₁=380 В. Двигатель развивает номинальную мощность на валу Р₂=20 кВт и имеет число полюсов 2р=10. Скольжение s = 2,5%; коэффициент мощности cos φ=0,88; КПД – η=0,93. Частота тока f₁=50Гц. Определить частоту вращения магнитно поля статора n₁; частоту вращения ротора n₂; ток двигателя I₁; номинальный момент вращения M; активную мощность, потребляемую двигателем из сети.

Задача 19

Трехфазный шестиполюсный асинхронный двигатель (2р = 6) подключен к сети с напряжением U₁=220 В, частотой f₁=50 Гц. Двигатель потребляет мощность Р₁=40 кВт при частоте вращения ротора n₂=96 об/мин и коэффициенте мощности cos φ=0,75. Суммарные потери мощности в двигателе ΣP=7кВт. Определить полезную мощность двигателя Р₂, КПД – η и полезный вращающий момент М; ток I₁, потребляемый двигателем; oпределить частоту вращения магнитно поля статора n₁ и скольжение s.

Задача 20.

Трехфазный асинхронный двигатель короткозамкнутым ротором работает в номинальном режиме и подключен к сети линейным напряжением U₁=380 В, промышленной частоты f₁= 50 Гц. Число полюсов двигателя 2р=12; номинальная мощность Р₂=45 кВт; частота вращения ротора n₂=490 об/мин; коэффициент мощности cos φ =0,91; КПД – η=0,91. Определить частоту вращения магнитно поля статора n₂, скольжение s; ток двигателя I₁, номинальный момент вращения M; активную мощность P₁, потребляемую двигателем из сети.

Задача 21.

Номинальная мощность генератора постоянного тока независимого возбуждения Р₂ = 50 кВт; КПД – η=0,86; ток во внешней цепи (ток нагрузки) I_н=I_а=109 А; напряжение возбуждения U_в=230 В, сопротивление цепи возбуждения R_в=40,9 Oм; сопротивление цепи якоря R_а = 0,15 Ом. Определить напряжение на зажимах генератора U; ЭДС генератора E; мощность Р₁, потребляемую генератором от первичного двигателя; сопротивление внешней цепи R_н, ток возбуждения I_в, суммарные потери мощности в генераторе ΣP. Начертить схему генератора независимого возбуждения.

Задача 22.

Двигатель постоянного тока последовательного возбуждения потребляет из сети напряжением U=220 В мощность Р₁=21,5 кВт. Частота вращения якоря n=1000об/мин; КПД – η=0,79; сопротивление цепи двигателя R_а+R_в=0,27 Ом. Определить полезную мощность на валу двигателя P₂; ток в обмотке якоря I_я; противо-ЭДС – Е в обмотке якоря, момент вращения двигателя М, суммарные потери мощности ΣP. Начертить схему генератора независимого возбуждения.

Задача 23

Генератор постоянного тока с параллельным возбуждением используется для питания специальной аппаратуры. Напряжение на зажимах генератора U=250 В; ток нагрузки I=95 А. Сопротивление обмотки якоря R_а=0,1 Ом; возбуждение R_в=50 Ом; КПД генератора η=0,9. Определить ЭДС генератора –Е; токи в обмотке якоря I_а и в обмотке возбуждения I_в; полезную мощность P₂, отдаваемую генератором; мощность P₁, затраченную двигателем на работу генератора. Начертить схему соединений генератора с параллельным возбуждением.

Задача 24.

Двигатель постоянного тока с параллельным возбуждением используется для приведения в движение центробежного насоса. Противо- ЭДС, которая индуцируется в обмотке якоря Е= 265 В; ток в обмотке якоря I_а=100 А; сопротивление обмотке якоря R_а=0,1 Ом; в обмотке возбуждения R_в=55 Ом; КПД – η=0,85; частота вращения якоря n=956 об/мин. Определить напряжение сети U, от которой питается двигатель; момент вращения двигателя М; ток в обмотке возбуждения I_в; общий ток двигателя I; мощности: на валу двигателя P₂ и потребляемую из сети P₁. Начертить схему соединений двигателя с параллельным возбуждением.

Задача 25.

Номинальная мощность генератора постоянного двигателя параллельного возбуждения Р₂ =100 кВт; КПД – η=0,9; ток во внешней цепи I=235 А; ЭДС генератора Е=460 В; сопротивление цепи возбуждения R_в=48 Ом. Определить мощность, потребляемую генератором P₁; напряжение на зажимах генератора U; сопротивление цепи якоря R_а; ток в обмотке возбуждения I_в; мощность в цепи возбуждения P_в. Начертить схему соединений генератора с параллельным возбуждением.

Задача 26.

Двигатель постоянного тока с параллельным возбуждением, полезная мощность которого Р₂=60 кВт, питается от сети с напряжением U=110 В, потребляя ток из сети I=608А. Ток в цепи возбуждения I_в=8 А, частота вращения якоря n=980 об/мин. Определить вращающий момент двигателя М; потребляемую двигателем мощность Р₁; КПД – η; ток в обмотке якоря I_а; сопротивление обмотки возбуждения R_в; мощность в обмотке возбуждения P_в. Начертить схему соединений двигателя параллельного возбуждения.

Задача 27.

Генератор постоянного тока потребляет от первичного двигателя мощность Р₁=84кВт; напряжение на зажимах генератора U=230 В; сопротивление внешней цепи R_н=0,7 Ом; сопротивление обмотки якоря R_а=0,03 Ом; ток в обмотке возбуждения I_в=10 А. Определить номинальную мощность генератора P₂; КПД – η; ток, отдаваемый во внешнюю цепь I_н; ток в обмотке якоря I_а; мощности в обмотках Р_я якоря и возбуждения Р_в; ЭДС генератора – Е. Начертить схему такого генератора.

Задача 28.

Генератор постоянного тока с независимым возбуждением отдает в нагрузку мощность P_2н=8,17 кВт. Сопротивление нагрузки R_н=1,62 Ом, сопротивление обмотки якоря R_а=0,12 Ом. КПД генератора η=0,85. Определить напряжение на зажимах генератора –U_н; ток нагрузки I_н; ЭДС генератора – Е; мощность Р₁ двигателя, приводящего генератор во вращение. Начертить схему такого генератора.

Задача 29.

Двигатель постоянного тока с последовательным возбуждением включен в сеть с напряжением U_н=220 В; частота вращения якоря n=1000 об/мин. КПД двигателя: η=0,882; ток в обмотке якоря I_а=77,3 А; противо – ЭДС Е=205,5 В. Определить полезный момент М двигателя; полезную мощность Р₂ на валу; потребляемую из сети мощность Р₁; сопротивление обмотки якоря и последовательной обмотки возбуждения R_а+R_по; суммарные потери мощности в двигателе ΣP. Начертить схему такого двигателя.

Задача 30.

Двигатель постоянного тока с параллельным возбуждением развивает номинальную мощность Р_н=40 кВт при напряжении U_н=220 В. КПД двигателя η_н=0,9. Частота вращения якоря n=800 об/мин; сопротивление обмотки якоря R_а=0,1 Ом, обмотки возбуждения R_в=55 Ом.

Определить потребляемую из сети мощность P_1н; ток двигателя I; суммарные потери мощности в двигателе ΣP; токи в обмотках якоря I_а и возбуждения I_в; номинальный момент М_н; противо-ЭДС – Е двигателя. Начертить схему такого двигателя.

Задача 31.

Потребитель подключен к однополупериодному выпрямителю и потребляет ток I_d=3 А при мощности Р_d=450 Вт. Подберите полупроводниковые диоды по допустимому току I_доп и обратному напряжению U_обр (табл. 1) для работы в лчестве вентилей такой схемы выпрямителя. Начертите схему выпрямителя и кратко опишите назначение ее элементов.

Задача 32.

От двухполупериодного выпрямителя, собранного по мостовой схеме, потребителю подается выпрямленное напряжение U_d=80 В при мощности Р_d=400 Вт. Подберите полупроводниковые диоды по допустимому току I_доп и обратному напряжению U_обр (табл. 1) для работы в качестве вентилей заданной схемы выпрямителя. Начертите схему выпрямителя и кратко опишите назначение ее элементов.

Задача 33.

От двухполупериодного выпрямителя, собранного по схеме с выводом от средней точки вторичной обмотки трансформатора, потребителю подается выпрямленное напряжение U_d=90 В при мощности Р_d=450 Вт. Подберите полупроводниковые диоды по допустимому току I_доп и обратному напряжению U_обр (табл. 1) для работы в качестве вентилей такой схемы выпрямителя. Начертите схему выпрямителя и кратко опишите назначение ее элементов.

Задача 34.

Подобрать диоды по допустимому току I_доп и обратному напряжению U_обр (табл. 1) для работы в качестве вентилей в схеме однополупериодного выпрямителя при значениях выпрямленного напряжения U_d=30 В и мощности Р_d=6 Вт. Начертите схему выпрямителя и кратко опишите назначение ее элементов.

Задача 35.

Выпрямленное напряжение выпрямителя, собранного по однополупериодной схеме, U_d=100 В при мощности Р_d=50 Вт. Подобрать полупроводниковые диоды по допустимому току I_доп и обратному напряжению U_обр (табл. 1) для работы в качестве вентилей такой схемы выпрямителя. Начертить схему выпрямителя и кратко опишите назначение ее элементов.

Задача 36.

От двухполупериодного выпрямителя, собранного пол мостовой схеме, потребителю подается выпрямленное напряжение U_d=30 В при мощности Р_d=300 Вт. Подберите полупроводниковые диоды по допустимому току I_доп и обратному напряжению U_обр (табл. 1) для работы в качестве вентилей такой схемы выпрямителя. Начертите схему выпрямителя и кратко опишите назначение ее элементов.

Задача 37.

Потребитель подключен к однополупериодному выпрямителю и потребляет ток I_d=8А при мощности Р_d=480 Вт. Подберите полупроводниковые диоды по допустимому току I_доп и обратному напряжению U_обр (табл. 1) для работы в лчестве вентилей заданной схемы выпрямителя. Начертите схему выпрямителя и кратко опишите назначение ее элементов.

Задача 38.

От двухполупериодного выпрямителя, собранного по схеме с выводом от средней точки вторичной обмотки трансформатора, потребителю подается выпрямленное напряжение U_d=25 В при мощности Р_d=250 Вт. Подберите полупроводниковые диоды по допустимому току I_доп и обратному напряжению U_обр (табл. 1) для работы в качестве вентилей такой схемы выпрямителя. Начертите схему выпрямителя и кратко опишите назначение ее элементов.

Задача 39.