ТЕМА 9. СИНТЕЗ ЗУБЧАСТИХ ЗАЧЕПЛЕНЬ
9.1. Основні поняття та задача
Зубчасте зачеплення – це вища кінематична пара, яка утворена послідовно взаємодіючими елементами двох ланок.
Зубчаста передача - це триланковий механізм, який складено з двох зубчастих коліс і стояка.
Зубчасті передачі призначені для передачі руху з одночасною зміною кутової швидкості та відповідно обертового моменту.
Рухомими ланками зубчастого механізму є зубчасті колеса, які утворюють зі стояком нижчу кінематичну пару, а між собою - вищу.
Елементами цієї вищої кінематичної пари є бокові поверхні зубців.
Лінія перетину бокових поверхонь зубців із площиною, перпендикулярною до осі обертання колеса, називається профілем зубця.
Менше з двох коліс називається шестернею, більше – колесом.
За формою колеса бувають: круглі, конічні, еліптичні.
Задача синтезу зубчастого зачеплення полягає в проектуванні елементів вищої кінематичної пари зубчастого зачеплення, тобто, профілів зубців, відповідно до заданих умов.
Умовами синтезу є:
l положення осей обертання (паралельні, пересічні, перехресні);
l необхідне передаточне відношення;
l якісні показники зачеплення (коефіцієнти перекриття, відносного ковзання, питомого тиску);
l експлуатаційні умови (плавність і безшумність роботи передачі, міцність, довговічність тощо).
9.2. Геометричні параметри зубчастого колеса
На рис. 9.1. наведена схема зубчастого зачеплення та позначення основних параметрів.
Термінологія надана за ГОСТ 16530-83.
Індекси для позначення коліс: 1 – шестерня; 2 – колесо.
 - міжосьова відстань – це відстань між центрами обертання коліс.
- міжосьова відстань – це відстань між центрами обертання коліс.
Ділильне коло – це базове коло, відносно якого визначаються всі геометричні параметри зубчастого колеса.
На рис. 9.1:
 - радіуси ділильних кіл шестерні та колеса;
- радіуси ділильних кіл шестерні та колеса;
 - радіуси початкових кіл шестерні та колеса;
- радіуси початкових кіл шестерні та колеса;
 - радіуси основних кіл шестерні та колеса;
- радіуси основних кіл шестерні та колеса;
 - радіуси кіл вершин шестерні та колеса;
- радіуси кіл вершин шестерні та колеса;
 - радіуси кіл западин шестерні та колеса;
- радіуси кіл западин шестерні та колеса;
 - товщини зубців шестерні та колеса.
- товщини зубців шестерні та колеса.

|
| Рис. 9.1. Геометричні параметри зубчастих коліс |
Основне коло – це геометричне місце центрів кривизни профілю зубця.
Крок зачеплення – це відстань по ділильному колу між однойменними профілями двох сусідніх зубців.
Позначимо:  - крок зачеплення;
- крок зачеплення; 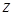 - число зубців;
- число зубців;  - діаметр ділильного колеса.
- діаметр ділильного колеса.
Тоді довжина ділильного кола:
 , ,
| (9.1) |
або:
 де де  - модуль зачеплення. - модуль зачеплення.
| (9.2) |
Модуль зачеплення – це відношення кроку зачеплення до числа 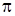 . Модуль зачеплення – головна характеристика зубчастих коліс. Вимірюється в міліметрах. Є величиною стандартною (ГОСТ 9563-60).
. Модуль зачеплення – головна характеристика зубчастих коліс. Вимірюється в міліметрах. Є величиною стандартною (ГОСТ 9563-60).
9.3. Основний закон зачеплення
Розглянемо фрагмент зубчастого зачеплення, що наведено на
рис. 9.2.
Виділяємо по одному зубцю шестерні 1 та колеса 2. Через т. 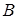 контакту профілів проводимо дотичну
контакту профілів проводимо дотичну  і нормаль
і нормаль  . З центрів коліс
. З центрів коліс  і
і  на нормаль
на нормаль  опускаємо перпендикуляри
опускаємо перпендикуляри  і
і 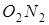 .
.
Точку 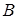 контакту з'єднуємо з центрами коліс
контакту з'єднуємо з центрами коліс  і
і  (це радіуси-вектори т.
(це радіуси-вектори т. 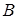 ).
).
Показуємо вектори лінійних швидкостей  і
і  (вони перпендикулярні до відповідних радіусів-векторів) і розкладаємо їх на нормальні та тангенціальні складові:
(вони перпендикулярні до відповідних радіусів-векторів) і розкладаємо їх на нормальні та тангенціальні складові:  і
і 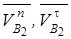 .
.
Умова сталості контакту профілів зубців, що забезпечує безперервність передачі обертального руху:
 . .
| (9.3) |
Розглянемо трикутники BO1N1 і BO2N2. Можна записати:

| (9.4) |

| (9.5) |
У свою чергу:
 ~
~  .
.
Тоді:

| (9.6) | ||

| |||
| Рис. 9.2. До основного закону зачеплення | |||
Умову сталості контакту (9.3) запишемо таким чином:

| (9.7) |
або
 . .
| (9.8) |
Уведемо поняття передаточне відношення - це відношення кутової швидкості ведучої ланки до кутової швидкості веденої ланки.
 , ,
| (9.9) |
де 
 - радіуси початкових кіл шестерні та колеса.
- радіуси початкових кіл шестерні та колеса.
Відносно полюса Р:
 . .
| (9.10) |
 . .
| (9.11) |
Але з векторного рівняння швидкості маємо:
 . .
| (9.12) |
Проте:
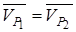 , тоді
, тоді 
Отже, т. Р – миттєвий центр обертання або полюс зачеплення.
Основний закон зачеплення:
Нормаль профілів зубців завжди проходить через миттєвий центр обертання, який ділить міжосьову відстань на відрізки, обернено пропорційні кутовим швидкостям.
Профілі зубців, які задовольняють основному закону зачеплення, називаються спряженими.
Основна вимога до зубчастих механізмів:
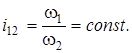
| (9.13) |
Отже:
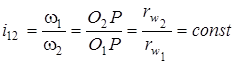 . .
| (9.14) |
Міжосьова відстань:

| (9.15) |
Інакше:

| (9.16) |
Отже:

| (9.17) |
Якщо при проектуванні зубчастого механізму задані  і
і 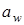 , то радіуси початкових кіл визначаються за формулами:
, то радіуси початкових кіл визначаються за формулами:

| (9.18) |
Оскільки профілі зубців перекочуються з ковзанням, то треба визначити швидкість ковзання  .
.
 Однак, відносно полюса Р швидкості рівні:
Однак, відносно полюса Р швидкості рівні:

Остаточно:
 . .
| (9.19) |
У полюсі зачеплення Р: 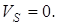
Коефіцієнти відносного ковзання:
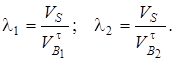
| (9.20) |
У полюсі зачеплення Р:  .
.
Висновки з основного закону зачеплення:
Профілями зубців можуть бути дві будь-які взаємообвідні лінії: пряма, парабола, гіпербола, евольвента тощо. Однак, профілі зубців мають відповідати ще й експлуатаційним умовам (технологічності, міцності, довговічності тощо), тому на практиці за профіль зубців приймають:
Ø евольвенту кола;
Ø циклоїдальні криві;
Ø дуги кола.
9.4. Види зачеплень (загальна класифікація)
9.4.1. За формою профілю зубця
l Евольвентні
Запропонував Леонард Ейлер (наприкінці  століття). Найбільш поширені. Забезпечують головну перевагу – сталість передаточного відношення.
століття). Найбільш поширені. Забезпечують головну перевагу – сталість передаточного відношення.
l Циклоїдальні
Застосовують переважно в приладобудуванні із-за складності у взаємозамінності.
l Зачеплення Новикова
Запропонував викладач академії ім. М.Є.Жуковського в 1948 р. Запатентоване в Швеції, Англії. Профіль зубця окреслений дугою кола. Зачеплення точкове, колеса тільки косозубі.
9.4.2. За положенням полюса зачеплення
l Зовнішнє зачеплення (рис. 9.3).
Полюс 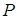 знаходиться між центрами обертання коліс
знаходиться між центрами обертання коліс  і
і  .
.
Міжосьова відстань:
 . .
| (9.21) |
Передаточне відношення:
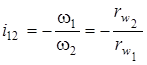 (напрям обертання змінюється). (напрям обертання змінюється).
| (9.22) |
Якщо відомі  і
і 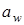 , то можна визначити радіуси початкових кіл:
, то можна визначити радіуси початкових кіл:
 ; ;  . .
| (9.23) |

| |
| Рис. 9.3. Схема зовнішнього зачеплення |
Швидкість ковзання:
 . .
| (9.24) |
l Внутрішнє зачеплення (рис. 9.4).
Полюс 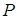 знаходиться поза центрами обертання коліс
знаходиться поза центрами обертання коліс  і
і  .
.

|
| Рис. 9.4. Схема внутрішнього зачеплення |
Міжосьова відстань:
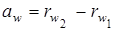 . .
| (9.25) |
Передаточне відношення:
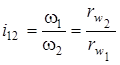 (напрям обертання не змінюється). (напрям обертання не змінюється).
| (9.26) |
Якщо відомі  і
і 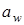 , то можна визначити радіуси початкових кіл:
, то можна визначити радіуси початкових кіл:
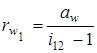 ; ;  . .
| (9.27) |
Швидкість ковзання:
 . .
| (9.28) |
l Рейкове зачеплення (рис. 9.5).
Обертальний рух шестерні перетворюється в поступальний рух зубчастої рейки.
Швидкість ковзання:
 . .
| (9.29) |

| |
| Рис. 9.5. Схема рейкового зачеплення |