Вторые производные и производные более высоких порядков.
Определение 1.6.Производная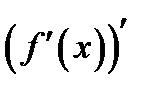 
от производной функции называется второй производной функции или производной второго порядка и обозначается формулой 
.
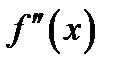Замечание. Вторые производные также можно записывать символами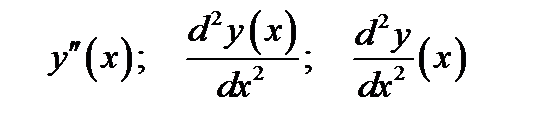 
Определение 1.7.Производная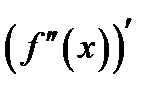 
от второй производной функции называется третьей производной функции или производной третьего порядка и обозначается формулой 
.
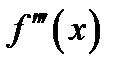Замечание. Производные 3-го порядка также можно записывать формулами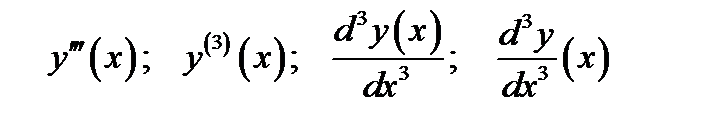 
Замечание.Производные n-го порядка определяются аналогично и записываются так
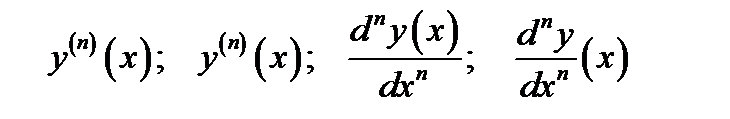
Пример 1.5.Вычислим производные второго, третьегои четвёртого порядков от функции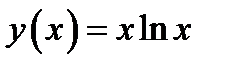 
. Решение.
Замечание.При дифференцировании многочленов порядок его производной понижается при каждом дифференцировании на единицу и поэтому любой многочлен всегда имеет конечное число ненулевых производных.
Пример 1.6.Вычислим все производные многочлена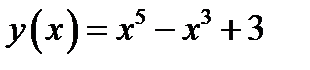 
.
Решение. 
Пример 1.7.Вычислим производные 
, где 
Решение. Используя правило дифференцирования произведения, получаем
Пример 1.8.Две материальные точки, массами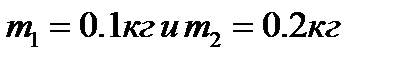 
, движутсяпрямолинейно со скоростями 
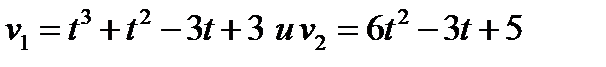. В какой момент времени значения сил, действующих на эти точки, окажутся равными.
Решение. При решении данной задачи, используем второй закон Ньютона: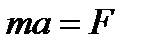 
. Ускорение
точки есть скорость изменения скорости. Действующие на точку силы равны, если ускорения этих точек равны. Следовательно,
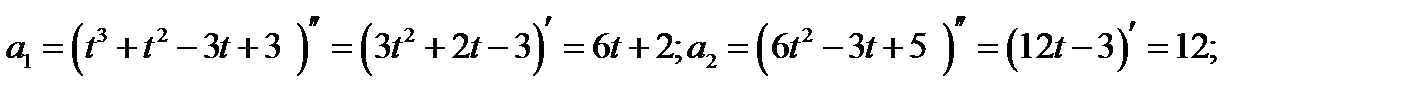Откуда
.
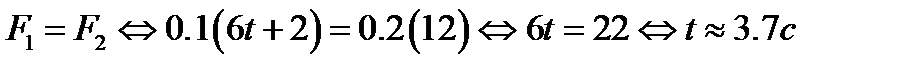Контрольные вопросы.
I. Дайте определения секущей и касательной прямых линий к графику .
II. Дайте определение средней и мгновенной скорости движения точки вдоль прямой.
III. Сформулируйте определение производной в точке. Каков геометрический и физический смысл производной функции в точке?
IV. Какие функции называются дифференцируемыми?
V. Будет ли дифференцируемая функция непрерывной функцией?
VI. Как определяется угол между графиками в точке их пересечения?
VII. Как вычисляются производные базовых элементарных функций с помощью
замечательных пределов?
VIII. Сформулируйте основные правила дифференцирования функции.
IX. Дайте определения второй и других старших производных. Какой геометрический смысл второй поизводной?
