Преобразование Галилея

Автор. Проводя вычисления в рассматриваемых выше задачах, мы всегда вводили систему отсчета. Но в разных системах отсчета одно и то же движение выглядит по-разному. При этом в одних системах отсчёта движение представляется проще, в других – сложнее. Если в системе отсчета любой процесс не зависит от местоположения тела, т. е. безразличен к смещению, то говорят, что пространство однородно. Если этот процесс не зависит от ориентации тела в пространстве, т. е. безразличен к повороту тела, то пространство считают изотропным. В случае равноправия всех моментов времени, мы будем считать время однородным. Справедлив закон инерции: тело, не взаимодействующее с другими объектами, сохраняет свою скорость неизменной. Именно поэтому такие системы назвали инерциальными, т. к. в них выполняется закон инерции.

В инерциальных системах отсчета одинаково поставленные опыты приводят к идентичным результатам независимо от того, где и когда они проводились и как при этом была ориентирована экспериментальная установка. Если система отсчета является неинерциальной, то соответствующие опыты могут давать разные результаты.

Существует бесконечное множество инерциальных систем отсчета, движущихся друг относительно друга прямолинейно и равномерно. Во всех инерциальных системах свойства пространства и времени одинаковы; все физические законы и явления тоже одинаковы при одинаковых начальных условиях. Так формулируется принцип относительности. Для механических явлений его сформулировал Галилей, позднее Эйнштейн дал более обобщенную формулировку, которую мы привели выше. Полная физическая эквивалентность всего множества инерциальных систем показывает, что не существует никакой одной "абсолютной" системы отсчета, которую можно было бы предпочесть другим.

В разных системах отсчета одно и то же движение выглядит по-разному. При этом в одних системах отсчета движение представляется проще, в других – сложнее.

Радиусы-векторы R₀ и r одной и той же точки в двух различных системах отсчета, одна из которых движется относительно первой со скоростью V, связаны соотношением.

R₀= r+ Vt (1.15)

 

 

Рис.1.5.1

 

Чтобы перейти в систему отсчета О₁, движущуюся прямолинейно и равномерно со скоростью V относительно наблюдателя (О – лабораторная система), необходимо сделать следующие преобразования:

r = R₀ – Vt (1.16)

V₁= V₀–V

а=а_0,

гдеV₀ , а₀ – соответственно скорость и ускорение частицы в лабораторной системе отсчета;V₁ и а – скорость и ускорение в системе отсчета, движущейся со скоростью V. Равенство (1.16) называют преобразованием Галилея, а соотношение (1.15) – обратным преобразованием Галилея.

Сохранилось любопытное предание, которое приписывают Диогену. Древнегреческий философ Зенон сформулировал знаменитую апорию (затруднение) под названием "Стрела". Это было главное доказательство Зенона против любого движения. Вот его суть. Стрела движется либо там, где она находится, либо там, где она не находится, третьего не дано. Второе отпадает, т. к. стрела не может двигаться там, где её нет. Значит, ей остается двигаться только там, где она находится. Но как тело может двигаться в пространстве, которое оно само заполняет? Ему просто некуда в нем двигаться! Выслушав Зенона, в качестве ответа Диоген стал расхаживать перед ним туда и обратно, демонстрируя движение. Однако Пушкин проницательно отметил:

Движенья нет, сказал мудрец брадатый.

Другой смолчал и стал пред ним ходить.

Сильнее бы не мог он возразить;

Хвалили все ответ замысловатый.

Но, господа, забавный случай сей

Другой пример на память мне приводит:

Ведь каждый день пред нами солнце ходит,

Однако ж прав упрямый Галилей.

Действительно, не всегда то, что человек видит или чувствует, является истиной. Наше восприятие далеко не совершенно.

Задача 1.8. «Мальчик, догоняющий автобус»

По прямому шоссе едет автобус с постоянной скоростью V. Мальчик заметил автобус, когда тот находился в точке А. Из какой области около шоссе мальчик сможет догнать этот автобус, если скорость мальчика U<V? Нарисуйте эту область для случая U=V/2.

Студент: – Задачи на преобразования Галилея мне всегда казались сложными.

Автор: – Это не случайно. Мне самому доставляет некоторое волнение разбор этого материала со студентами. Насколько проста и понятна эта теория, и какие сложные бывают варианты её применения! Дело в том, что при решении задач на эту тему приходится использовать укрупнённые дидактические единицы, как сказали бы методисты. Одновременно выполняется целая совокупность разнообразных математических операций и физических рассуждений: переход в движущуюся систему отсчета и возврат в лабораторную систему. При этом необходимо уметь переписать все необходимые уравнения в новых переменных. Немалую трудность вызывает определение критерия оптимальности задачи, а во многих заданиях просят найти именно максимальное или минимальное значение какой-то физической величины. Выбор удобной системы отсчета требует значительного опыта, а порой интуиции.

Студент: – Сначала нарисуем исходные положения участников движения. Пусть в начальный момент автобус находился в точке А, мальчик – в крайней точке В, от которой он еще сможет догнать автобус. Место их встречи обозначим С. По нашему построению, 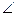ВАС= α – максимально возможный.

 

 

 

 

Если мальчик начнет движение из точки В₁, находящейся вне угла α, то он не успеет добежать до автобуса. Первые трудности возникают в определении направления движения ВС. Пока непонятно, под каким углом β следует бежать мальчику.

Автор: – Известны способы решения такого рода задач, когда требуется найти оптимальное значение какого-либо параметра. Для нахождения минимального времени можно составить функцию t(β) и, вычислив производную, получить значение β. Но эта задача решается проще без использования свойств производной. Мы разберём два способа решения. Первый – чисто математический. Составьте вспомогательную функцию f(β)=t₁/t₂, где t₁ – время движения автобуса до точки С, а t₂ – время, затраченное мальчиком. По смыслу движения нам необходимо, чтобы f(β) была максимальна.

Студент:

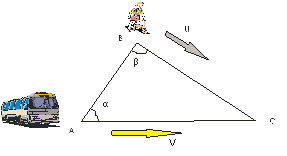
f(β)= t₁/t₂ = · 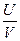. (1.17)

По теореме синусов для ΔАВС имеем:

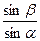= . (1.18)

Получим, f(β)= 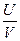· 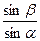. Понятно, что f(β) имеет максимум, если sinβ наибольший, т. е. sinβ=1, следовательно, β=π/2. А значение функции f=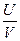 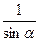. Мальчик догонит автобус при выполнении условия f≥1. Или sinα≤ 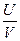. В частности, при U=V/2 имеем α≤ π/6.

Автор: – Следует заметить, что такая же область, ограниченная углом π/6, существует и в нижней полуплоскости. Поэтому окончательный ответ такой.

◄Область, из которой мальчик догонит автобус, есть угол с вершиной в точке А, равный 2arcsin 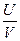, биссектриса этого угла лежит на траектории автобуса►.

Как Вы уже поняли, ключевым моментом этого способа решения было удачное введение функции f(β), что требует определённой исследовательской интуиции, которая формируется и развивается только в ходе решения подобных задач.

Рассмотрим более "физичный" вариант анализа данного движения, основанный на преобразовании Галилея. Перейдите в систему отсчёта, связанную с движущимся автобусом, и рассмотрите возможные направления относительной скорости мальчика.

Студент: – Система отсчёта, в которой автобус покоится, движется вправо со скоростью V. Чтобы перейти в неё, добавим ко всем объектам, участвующим в движении, скорость –V. Результирующая скорость мальчика находится как векторная суммаU + (–V )=U₁ .

 

 

Рис. 1.5.2

 

Автор: – Куда может быть направлена скоростьU₁?

Студент: – Думаю, точно на автобус. Потому что в случае, если линия скоростиU₁ пересечётся с траекторией левее точки нахождения автобуса, это будет означать, что мальчик опоздал. А в случае пересечения справа – мальчик попадёт на шоссе с опережением. Значит, у него есть "резервы" по дальности стартового положения.

Автор: – Хорошо. Но под каким углом может бежать мальчик?

Студент: – Я затрудняюсь ответить. Есть два варианта суммы U + (–V), и оба они дадут вектор, направленный вдоль оси, соединяющей автобус и мальчика.

 

 

Рис. 1.5.2а

 

Автор: –Напомню, что мы исследуем пограничную ситуацию, т. е. нас интересует минимальная скорость, при которой мальчик еще догонит автобус. Из всего семейства векторовU, которое Вы изобразили на рис. 1.5.2а, выберите вектор с наименьшей длиной.

Студент: – Я, кажется, догадался. Это будет вектор, перпендикулярный направлению АВ. Значит, по подобию ΔАВС тоже прямоугольный. Получается, что направление движения мальчика в лабораторной системе отсчёта составляет угол 90^о с линией "мальчик – автобус", что мы уже получали чисто математически. Таким образом, величина угла, в пределах которого мальчик успеет догнать автобус, находится из равенства:

sinα= .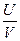

Автор: – Если сопоставить оба наших метода решения, то видно, что как только мы положили значение функции f(β)=1 и минимизировали неявную зависимость U(β), то сразу получили туже пропорцию, которую Вы написали из геометрических соображений, правильно определив направление вектораU.

Действительно,

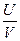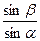· =1, U=V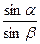 U_min=Vsinα.

В качестве дополнительного задания исследуйте следующую ситуацию.

Пусть в начальный момент времени мальчик находился на расстоянии Н до шоссе. На каком минимальном расстоянии от точки D может находиться автобус в начальный момент, чтобы мальчик его догнал?

Студент: – Это уже просто. АD=Нctgα=Н /U.

Время встречи найдем так:

t=ВС/U=H/(U cosα)=НV/( ·U).

Автор: – Как видно из полученных соотношений, они имеют смысл только при V>U. Если чисто теоретически предположить, что скорость мальчика больше, чем скорость автобуса, то он в любом случае догонит автобус. А как понять то, что время до встречи стремится к бесконечности при скорости U приближающейся к V?

Студент: – Если U ≈ V, то α ≈ π/2. Следовательно, прямая ВС почти параллельна шоссе. Это и означает, что место встречи будет очень далеко и для этого потребуется значительное время.

Задача 1.9. "Самонаводящиеся" черепашки.

Четыре черепашки расположились в вершинах квадрата со стороной а. Затем они устроили игру в "догонялки". Но преобразований Галилея черепашки в школе не усвоили, поэтому одновременно начали ползти друг к другу со скоростью V, точно направленной на соседа, расположенного по часовой стрелке. Где и когда встретятся наши "спринтеры"?

 

 

 

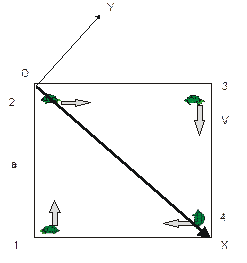
Студент: – Необходимо найти удобную систему отсчёта.

Автор: – Попробуйте связать ее с одной черепашкой. И найдите скорость приближения её к центру квадрата.

Студент: – Разложим скорость черепашки на составляющие вдоль оси ОХ, направленной от черепашки к центру квадрата, и вдоль оси ОY, перпендикулярной ОХ. За приближение к центру отвечает только Х–компонент скорости V_х=Vcos(π/4)=V/ . Можно заметить, что исследуемая система при повороте на угол π/2 переходит в себя, т. е. обладает симметрией относительно поворота на 90^о. Из этого следует, что черепашки так и останутся в вершинах квадрата, т. к. он обладает такой симметрией. Ось ОХ будет лежать на диагонали этого квадрата в любой момент времени. Значит, черепашка достигнет центра через время t= S/V_х = (а/ ):(V/ )= а/V. Такая же судьба ожидает и всех остальных участников гонки, поэтому они все встретятся в центре квадрата. Итак, получаем ответ:

◄t= а/V►.

Автор: – Есть и другие способы, позволяющие решить эту задачу. Рассмотрим сближение двух соседних черепашек через бесконечно малый промежуток времени Δt. Первая черепашка приблизится к положению второй на расстояние VΔt. В свою очередь, вторая черепашка движется перпендикулярно первой и за малое время Δt почти не удаляется от неё. Так будет происходить в любой момент времени. Значит, расстояние между черепашками уменьшается со скоростью V. Эту скорость можно назвать скоростью сближения. Начальное расстояние между соседними черепашками а. Ответ следует незамедлительно: t= а/V.

Задача 1.10. «Опасный угол»

Снаряд, летящий со скоростью V, разрывается на множество осколков. В системе отсчета снаряда, осколки имеют одинаковую скорость U и равномерно разлетаются во все стороны. Найти область, которая может быть поражена этими осколками.

 

 

Студент: – Так как осколки разлетаются во все стороны и с одинаковыми по модулю скоростями, то в системе снаряда мы получим векторы скорости, концы которых образуют окружность. Чтобы найти скорость осколка в лабораторной системе отсчета, сложим векторыV иU. Получим результирующую скорость. Но как исследовать все эти векторы?

Автор: – Вы хорошо применили преобразование Галилея для скоростей, но правило параллелограмма для сложения скоростей здесь не очень удобно. Попробуйте переделать чертёж, применив правило треугольника.

 

 

Студент: – Из этого рисунка видно, что получилось целое семейство векторов скоростей разлетающихся осколков. Скорость "пограничного" осколка направлена по касательной к окружности, которая представляет собой совокупность концов векторов скоростей всех осколков. Обозначим предельный угол разлета φ. Видим, что sinφ=U/V. Все другие осколки полетят под углом, меньшим чем φ. Такой же угол можно отложить и в противоположную сторону. Значит, область поражения представляет собой угол, равный 2φ, биссектриса которого лежит на траектории снаряда.

Автор: – Проанализируйте ситуацию, когда U>V.

Студент: – Странно, синус превысил единицу. Хотя в этом случае мой рисунок надо переделать. Получится, что осколки вполне могут лететь даже в направлении, противоположном скорости снаряда. Значит, везде находиться не безопасно.

Автор: Окончательно имеем следующий ответ для границы поражения.

◄При U≤V – это конус с углом между высотой и образующей φ, вершиной в месте разрыва снаряда и высотой, лежащей на траектории снаряда,

sinφ =U/V.

При U>V – все направления будут поражены ►.

 

Задача 1.11. «Когда кошка догонит мышку?»

Из угла комнаты выбегает мышка со скоростью U, направленной вдоль стены. В другом углу, находящемся на расстоянии Н от стартового положения мышки, притаилась кошка, которая тут же бросилась догонять мышку со скоростью V, направленной всегда строго на объект преследования. Через какое время кошка приступит к своему завтраку?

 

 

Автор: – Это задача знаменита наличием оригинального и неочевидного способа решения. Дело в том, что простая запись дифференциальных уравнений, описывающих скорость и координаты кошки, дает сложную систему. Но преобразования Галилея позволяют ответить на вопрос задачи без знания траектории кошки. Одна подсказка: удобно рассмотреть произвольную точку траектории кошки в какой-то момент времени t. Далее надо записать скорость сближения участников движения. Для этого удобно обозначить модуль расстояния между кошкой и мышкой r и спроецировать на ось "кошка – мышка" все скорости. Тем самым Вы получите интересное дифференциальное уравнение.

Студент: – Если я правильно понимаю, то скорость сближения способствует уменьшению относительного расстояния между участниками движения. Значит, dr/dt имеет отрицательный знак. Следовательно,

dr/dt = –V_сб,

где V_сб – скорость сближения, с которой сейчас разберемся. Кошка имеет всегда одну и ту же проекцию скорости на ось, соединяющую движущиеся объекты. Величина этой проекции V. Спроецируем скорость мышки на эту ось, получим Ucosφ. Следовательно, скорость сближения равна

V_сб =V – Ucosφ.

Наше дифференциальное уравнение принимает вид:

dr/dt = –V + Ucosφ.

Автор: – Теперь выразите cosφ из разложения скорости кошки по компонентам.

Ученик:

V_x = Vcosφ.

Значит,

cosφ= V_x / V= .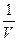

В итоге получим

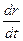= –V+ .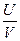

Автор: – Проинтегрируем левую и правую части уравнения по переменной t в пределах от 0 до Т, где Т – время, которое пройдет до приятной встречи кошки с мышкой. В левой части получим:

= = –Н.

Правая часть преобразуется так:

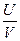
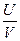
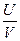– + = – + = –VT+ X_{o .}

Здесь введено обозначение X_o – полное расстояние, которое пробежит мышка. Можно сказать, что X_o – конечная координата мышки вдоль оси ОХ. Раз мышка двигалась с постоянной скоростью, то X_o =UT.

Студент: – Теперь легко довести вычисления до ответа. Сравнивая преобразованные левую и правую части, получаем

– Н= –VT+ T=( –V)T,

Получаем ответ:

◄T= V►.

Ответ имеет смысл только при условии V>U.

Второй способ решения.

Обозначим положение кошки К, а мышки М. Проекцию точки К на ось ОХ (тень кошки) обозначим К_х. Точка К_х будет двигаться со скоростью V_x = Vcosφ. Значит, мышка удаляется от точки К_х со скоростью V₂=U- Vcosφ. Эта скорость будет иметь сначала положительное, а потом отрицательное значение. Учитывая

V_сб =V – Ucosφ, избавимся от cosφ и получим:

, V₂U – U²=V∙V_сб – V²

U² - V²=V₂U - V∙V_сб=

=U - V 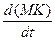=d(U∙MK_x+V∙MK)/dt.

U² - V²<0, значит, величина U∙MK_x+V∙MK убывает с постоянной скоростью U² - V².

В начальный момент U∙MK_x+V∙MK =VH. В конце пути мышки (начале завтрака кошки) U∙MK_x+V∙MK =0. Исходя из определения производной, имеем:

VH/T= U² - V²

Получаем тот же ответ.

Как видим, единственным персонажем наших задач, который в состоянии догнать цель, имеющую скорость большую, чем сам догоняющий, был мальчик, из задачи 1.8. Это потому, что он хорошо освоил преобразования Галилея.

История.

Эрнст Резерфорд пользовался следующим критерием при выборе своих сотрудников. Когда к нему приходили в первый раз, Резерфорд давал задание. Если после этого новый сотрудник спрашивал, что делать дальше, его увольняли.

 

Задачи

5.1. Человек, сидящий в закрытом вагоне поезда, идущего с постоянной скоростью, подбрасывает мяч вверх (в своей системе отсчета). В каком месте упадет мяч? Как изменится ответ в случае, если вагон: а) ускоряется, б) тормозится, в) выполняет поворот, д) вагон движется с постоянной скоростью, но испытывает сопротивление воздуха?

5.2. Капли дождя из-за сопротивления воздуха падают с постоянной скоростью V, перпендикулярной поверхности земли. Как необходимо расположить цилиндрическое ведро, находящееся на движущейся горизонтально со скоростью U платформе, чтобы капли не попадали на стенки?

5.3. Начальные положения и векторы скоростей двух кораблей заданы на рисунке. Корабли движутся без ускорения. Как найти наименьшее расстояние между ними?

5.4. Буер представляет собой парусные сани. Он может двигаться лишь по линии, по которой направлены коньки. Ветер дует со скоростью V, перпендикулярной его движению. Парус же составляет угол 30^º с направлением движения. Определите максимально возможную скорость буера.

5.5. При упругом ударе тела о неподвижную стенку скорость V меняется лишь по направлению. Определите, на какую величину изменится после удара скорость этого тела, если стенка движется: а) со скоростью U навстречу телу; б) со скоростью W< V в направлении движения тела.

5.6. Какой будет длительность полёта самолёта из Новосибирска в Москву и обратно, происходящего по прямой, если в течение всего полёта дует ветер под углом a к трассе со скоростью U? Скорость самолёта относительно воздуха V, длина трассы L. При каком направлении ветра длительность рейса максимальна?

5.7. Тело влетает горизонтально со скоростью V в пространтрассы L. При каком направлении ветра длительность рейса максимальна?

5.7. Тело влетает горизонтально со скоростью V в пространство между двумя вертикальными плоскостями, которые движутся со скоростью U. Определите скорость тела после n-го удара о переднюю стенку. Расстояние между стенками L. Удары абсолютно упругие.

5.8. Идёт “вертикальный” дождь. Скорость капель U. По асфальту со скоростью V скользит мяч. Во сколько раз на него попадает больше капель за секунду, чем на такой же неподвижный мяч? Изменится ли ответ, если мяч не круглый?

5.9. Мальчик, который может плавать со скоростью, в два раза меньшей скорости течения реки, хочет её переплыть так, чтобы его снесло вниз по течению как можно меньше. Под каким углом к берегу он должен плыть? На какое расстояние его снесёт, если ширина реки 200 м?

5.10. На рисунке (вид сверху) изображены шлейфы дыма, тянущиеся от двух паровозов, которые движутся по прямолинейному участку дороги со скоростями V₁ и V₂ (V₁>V₂.). С помощью геометрических построений найдите вектор скорости ветра.

 

 

 

§ 1.6