Дедукция и индукция
Множество и операции над ними
Множеством именуется некоторая совокупность элементов, объединенных
по какому-либо признаку. Если есть такая совокупность, разумеется, как единое целое, говорят, что имеют дело с множеством.
Приведенное определение не может рассматриваться как математически строгое, поскольку понятие множества является исходным, на основе него стоятся остальные понятия математики. Тем не менее, из при веденного определения ясно, как можно говорить с множестве, например, действительных чисел или множестве плоских фигур.
Если множество состоит из конечного числа элементов, оно называется конечным. Остальные множества называются бесконечными. Для множества используются следующие обозначения:
А = {a,b,c,d}
Приведенное обозначение записано для множеств А, состоящего из элементов a, b, c, d.
Конечные множества можно задать перечнем их элементов, бесконечные –
нельзя. Обычно бесконечное множество задают, указывая на свойства, которым
обладают все элементы данного множества, при этом подчёркивают, что таким свойством не обладают никакие элементы, не входящие в это множество. Такое
свойство называется характеристическим для рассматриваемого множества.
Множество, в котором не содержится ни одного элемента, называется пустым. Обозначается оно знаком ø
Множества, состоящие из одних и тех же элементов , называют совпадающими. Например, совпадают два конечных множества, которые отличаются друг от друга порядком их элементов. Если элемент а принадлежит множеству А, то пишут :
А є А
В противном случае пишут :

Если одно множество является частью другого множества, говорят, что первое множество является подмножеством второго. Если первое множество обозначить А, а второе В, то обозначение такое:

Для любого множества А справедливы высказывания: множество А является подмножеством самого себя. Пустое множество является подмножеством любого
множества.
В качестве примера можно привести высказывание о том, что множество всех ромбов является подмножеством множества параллелограммов.
Над множествами определяют операции, во многом сходные с арифметическими. Рассмотрим понятие таких операций только над двумя множествами А и В, которые являются разнообразными подмножествами одного и того же множества U. Последние назовём универсальным множеством. Операции над множествами удобно интерпретировать геометрически с помощью диаграмм Эйлера –Венна (рис. 1-4)
Определение 1.Пересечением множеств А и В называют их общую часть С. Другими словами, пересечение множеств А и В образуют элементы, принадлежащие равно как и А, так и В

Такое множество обозначают :


Определение 2. Объединением множеств А и В, называют С, составленное из элементов, принадлежащих хотя бы одному из этих множеств
Определение 3. Разностью множеств А и В называют множество
С = В \ А

Составленное из элементов, принадлежащих множеству В, но не принадлежащих множеству А
Разностью U \ A называется дополнением множеству А до универсального множества U и обозначается А = U \ A
Геометрическая интерпретация множества А дана на следующем рисунке: 
Если применять операции объединения и пересечения – к подмножествам некоторого множества D, то снова получается подмножества того же множества D.
Операции объединения и пересечения обладают многими свойствами, похожими на свойства операций сложения и умножения чисел. Например, пересечения и объединение множеств обладают свойствами коммутативности и
ассоциативности. Пересечение дистрибутивно относительно объединения, то есть для любых множеств А, В и С верно соотношение 
Примеры множеств. Примеров множеств можно привести сколько угодно. Так, можно говорить о множестве всех букв книги, причем одна и та же буква на разных страницах или разных строках одной страницы считается за два различных элемента множества, о множестве всех людей земного шара, причем надо сделать предположение, что в рассматриваемый момент времени никто не рождается и не умирает, о множестве молекул воды в данном стакане и т.д.
Все это – конечные множества. Приведем некоторые примеры бесконечных множеств, кроме упоминавшихся выше множеств натуральных чисел, четных натуральных чисел, рациональных чисел, действительных чисел и др.
Пусть а и b – два действительных числа, причем a < b. Множество всех действительных чисел х, для которых a ≤ x < b, называется отрезкомс концами a,b и обозначается [ a, b ]. Множество (a,b ) всех х, для которых a < x < b называется интервалом с концами a,b. Далее полуинтерваламиназывается множество [ a,b) , тех х, для которых a ≤ x < b, и (а, b], тех х, для которых a < x ≤ b.
Введем ещё два символа : +∞ ( плюс бесконечность ) и -∞ ( минус бесконечность). Они не являются числами и вводятся для удобства записи. Тем не менее для более легкого обращения с ними условимся говорить, что +∞ больше, а
-∞ меньше любого действительного числа. Тогда можно ввести обозначения, аналогические приведенным выше, для бесконечных полуинтрвалов и интервалов. Именно: [ a, + ∞) – множество чисел х, для которых а ≤ х (-∞,b]- множество чисел х, для которых х ≤ b, (а, +∞) – множество чисел для которых а < х, ( -∞, b) – множество чисел х, для которых x < b, ( -∞, +∞ ) – множество всех действительных чисел.
Упражнения:
1. Записать множества, перечислить их элементы:
а). положительные числа, кратные 7 и меньше 60;
б). решите уравнение  - 3x - 10 = 0
- 3x - 10 = 0
2. Записать все подмножества М = {5,12,6}
3. Найти объединение и пересечение множеств решений уравнений  -3x+2=0 и
-3x+2=0 и 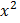 - 1 = 0
- 1 = 0
4. Найти разность А\В и В\А, если А = {а,b,c,d} и В = {b,d,p,q,r}
5. Пусть А – множество целых чисел, которые делятся на 4, В- множество целых чисел, которые делятся на 3. Какие из чисел 9,0,-24,-53,1242048 входят во множество А U В ?
6. Пусть множество, состоящие из 20 студентов, которым нужны проездные билеты на троллейбус, В – множество проездных билетов на троллейбус. Будет ли А=В. Обосновать ответ
7. Найти сумму множеств:
а). А- { четные числа}, В - {натуральные степени числа 2};
б). М= {простые числа}, Р = {нечетные числа}.
8. Найти:
а). Пересечение множеств М= {простые числа, меньше 40}, Р={нечетные числа, больше 14}
б) разность множеств К = {1,2,3,4,5,6,7} и L = {2,4,6}.
9. Запишите с помощью фигурных скобок множество:
1). Букв в слове «алгебра» 3).Нечетных однозначных натуральных чисел
2). Частных однозначных натуральных чисел 4). Однозначных простых чисел.
2. По какому характеристическому свойству записаны такие множества:
а). {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}
б). {январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь }
в). {Австралия, Азия, Америка, Антарктида ,Африка, Европа }
г). {до, ре, ми, фа, соль, ля, си}
10. Приведите примеры пустых множеств:
11. А- множество четных натуральных чисел, расположенных между числами 25 и 35. Запишите множество А с помощью фигурных скобок. Какие из чисел 18, 28, 30,40 принадлежат множеству ? Ответ запишите с помощью знаков
12. Запишите с помощью фигурных скобок и обозначьте множество:
а). натуральных делителей числа 12
б). натуральных делителей числа 30
в). целых делителей числа 6
г). простых делителей числа 12
13. Известно, что М = {1,2,5}, N = {1,4,5,7,9}, К = {4,7,9}
Запишите с помощью фигурных скобок или знака ø
а). пересечение М и N е). объединение N и К
б). пересечение М и К ж). разность М и N
в). пересечение N и К з). разность М и К
г). объединение М и N и). разность N и К
д). объединение М и К к). дополнение К и N
14. Объясните почему выполняется равенство:
1). А U ø = A
2). А U А= А
15. Часть жителей города говорит только по–украински, часть только по-
русски, а часть на двух языках. По-украински говорит 95 % жителей, а по-русски 85%. Сколько процентов жителей города говорит на двух языках ?
15. Докажите равенство множеств и проиллюстрируйте его с помощью кругов Эйлера – Вена:
1). А\В = А (АΩВ)
2). АΩ (В\С) = (АΩВ) \ (АΩС)
16. Запишите множество всех правильных дробей  , где а є А, b є B и
, где а є А, b є B и
А= {2,3,4,6}, В= {1,3,4,5,6}
17. Какие трёхзначные числа можно записать, если:
А = {3,1,2} – множество цифр для обозначения сотен;
В = {2,8} –множество цифр для обозначения десятков
С = {5,7} – множество цифр для обозначения единиц
Сколько таких чисел получим ? Попытайтесь сформулировать общее правило подсчёта количества таких чисел, если множество А содержит m элементов (0
а). множество В- n элементов, множество С – k элементов.
18. Изобразить на координатной прямой промежуток:
1). ( -4, 2); 5). [-4, +∞]
2). [ -4,2] 6). (-4, +∞)
3). [-4,2) 7). (-∞, -4)
4). (-4,2] 8). (-∞, -4]
19. Изобразить на координатной прямой и записать промежуток, заданных неравенством:
1). Х < 3 5). 0 < x < 9
2). X > -5 6).  < = x < = 4
< = x < = 4 
3). X < = -2 7). -3,8 < x < = 6,4
4). X = > 1 8). 0,1 < = x < 604
8
20) Записать все целые числа, принадлежащие промежутку:
1). [4; 8] 2). (3; 7; 9 ] 3). [ -4,8; 2 ] 4). (-3; 3 )
21). Найти наименьшее целое число, принадлежащие промежутку:
1) [-10; -5 ] 2). (6; 12) 3). (11,2; +∞) 4).[13; + ∞)
22). Показать на координатной прямой и записать пересечение промежутков:
1). [ -2; 6 ] и [ 3 8 ] 2). [ 4; 7 ] и (4; 9 ] 3). (4,3; + ∞ )
4). [ - ∞; 3,7 ) и [ 3,9; +∞) 5). [ 10; -∞) и [ 13,4; +∞) 6). (-∞;3,7) и (3,9; +∞)
23. Показать на координатной прямой и записать объединение промежутков :
1) [2; 7,4 ] и (3;9) 2). [2; 7,] и (4;9] 3). (-∞;5) и (2;8,1 )
4) [3;7) и (7;+∞] 5). (-∞; 10) и (6,4; +∞) 6). (-∞; 3,7) и (3,9; +∞)
Дедукция и индукция
Индуктивные рассуждения
«По одной капли воды … человек, умеющий мыслить логически, может сделать вывод о существование Атлантического океана или Ниагарского водопада, даже если он не видел ни того, ни другого и никогда о них не слыхал…
По ногтям человека, по его рукам, обуви, сгибу брюк на коленях, по утолщениям кожи на большом и указательном пальцах , по выражению лица и обшлагам рубашки – по таким мелочам не трудно угадать его профессию. И можно не сомневаться, что все это вместе взятое, подскажет сведущему наблюдателю верные выводы»
9
Эта цитата из программной статьи самого знаменитого в мировой литературе сыщика- консультанта Шерлока Холмса. Исходя из мельчайших деталей, он строил логически безупречные цепи рассуждений и раскрывал запутанные преступления, причем зачастую не выходя из своей квартиры на Бейкер-стрит. Холмс использовал созданный им самим дедуктивный метод, ставящий, как полагал его друг доктор Уотсон, раскрытие преступлений на грань точной науки.
Конечно, Холмс несколько преувеличивал значение дедукции в криминалистике, но его рассуждения о дедуктивном методе сделали свое дело. «Дедукция» из специального и известного только немногим термина превратилась в общеупотребительное и даже модное понятие. Популяризация искусства правильного рассуждения, и прежде всего дедуктивного рассуждения, не - меньшая заслуга Холмса, чем все раскрытые им преступления. Ему удалось «придать логике прелесть грезы, пробирающейся сквозь хрустальный лабиринт возможных дедукций к единственному сияющему выводу» ( В. Набоков)