Следите за тем, чтобы грузы на стержнях маятника были надежно закреплены.

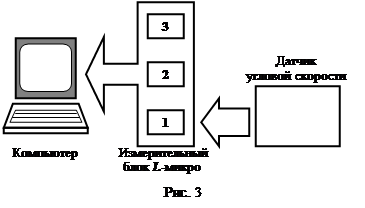
2. Подключите измери­тельный блок L-микро к разъ­ему последовательного порта компьютера и к сети (220 В, 50 Гц). Кабель датчика угло­вой скорости включите в разъем 1 канала блока - рис. 3. Включать в сеть измерительный блок L-микро можно только после его подключения к разъему последовательного порта компьютера.

 
 

 

 


3. Вклю­чите тумблер питания изме­рительного блока. Запустите программу L-рhуs.ехе,выберите пункт меню«СПИСОК ОПЫТОВ» и в появившемся на экране списке выбе­рите лабораторную работу«Определение моментов инерции тел».
4. Приступите к проведению измерений. Для этого необходимо:

а) намотать нить на катушку в один слой так, чтобы перегрузок, привязанный к нити, поднялся почти до уровня катушки. После этого удерживать маятник рукой, не давая ему начать враще­ние.

б) включить режим регистрации данных компьютером. Для этого выбрать пункт меню «ЗАПУСК» и опустить маятник. Запись данных будет продолжаться около 5 секунд.Вращение маятника следует остановить после того, как перегрузок коснётся стола.

в) провести первичную обработку данных появившихся на экране в виде графика зависимости угловой скорости вращения маятника Обербека от времени. Оставьте на графике участок, относящийся к равноускоренному движению системы. Для этого уберите точки, не относящиеся к периоду равноускоренного движения системы (соответствующие движению системы после того, как перегрузок на нити достигает поверхности стола). Перемещение курсора производится с помощью мыши или клавиш, а выбор интервала осуществляется при нажатой и удержи­ваемой кнопке мыши. (Чтобы вернуться к отображению всего графика, нажмите на графике правой кнопкой мыши, и выберите в меню пункт«ПОКАЗАТЬ ВЕСЬ ГРАФИК».)

По определению угловое ускорение определяется как тангенс угла наклона графика зависимо­сти угловой скорости от времени (так графически интерпретируется производная любой функции). Компьютерная программа строит прямую, наилучшим образом аппрок­симирующую экспериментальные данные и определяет ее угловой коэффициент (коэффициент e в уравнении прямой w=w0 + et ). Для этого курсор необходимо навести на соответствующую точку графика, после чего нужно нажать правую кнопку мышки и выбрать в появившемся на экране меню пункт«ПРОВЕСТИ ПРЯМУЮ».

г) действия, описанные в п.п. а) - в) необходимо повторить три раза. Результаты измерений внесите в таблицу 3.

д) снимите грузы со спиц и, вновь выполнив п.п. а) - г), получитеновые значения ускорения маятника Обербека. Результаты измерений занесите в таблицу 3.

5. Обработайте результаты экспериментов. Для этого:
а) пользуясь формулой (6) и значением rСР, вычислите три значения момента инерции I1 крестовины с грузами, а также его среднеарифметическое значение I1СР. Результаты занесите в таблицу 3.

б) пользуясь формулой (7) и значением rСР, вычислите три значения момента инерции I2 крестовины без грузов, а также его среднеарифметическое значение I2СР. Результаты занесите в таблицу 3.

в) рассчитайте DI1 иDI2 - ошибки измерений I1 иI2. Так,

 

DI1= a ,

DI2= a .

 

Здесь a -коэффициент Стьюдента, значения которого можно найти в таблице, приведённой в Приложении к настоящему сборнику (см. также методические указания [3]). Величину доверительной вероятности при выборе коэффициента Стьюдента по этой таблице примите рав­ной 0,95.

Таблица 3

Номер измерения rСР
Радиус маховика r, м        
Масса перегрузка mП, кг :
 
I. ВРАЩЕНИЕ С ГРУЗАМИ НА КОНЦАХ СПИЦ:
Массы грузов, кг m1 = m2 = m3 = m4 =
Расстояния до оси, м R1 = R2 = R3 = R4 =
 
Номер измерения  
e1, рад/с2        
I1, кг×м2       I1СР =
 
II. ВРАЩЕНИЕ БЕЗ ГРУЗОВ:
Номер измерения  
e2, рад/с2        
I2, кг×м2       I2СР =
 
III. ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ГРУЗОВ:
Эксперимент: Iг = I1СР- I2СР , м  
Расчет Iг*по формуле (10)  
           

 
6. Результат вычислений DI1и DI2округлите до первой значащей цифры, после чего округлите полученные ранее значения I1СР и I2СР до того же разряда, что и DI1и DI2.

7. Подставив в формулу (9) округлённые значения I1СР и I2СР, вычислите, среднее значение момента инерции грузов IгСР .

8.Ошибку измерения Iг рассчитайте по формуле: DIг = DI1+ DI2.

9. Используя соотношение (10), рассчитайте теоретическое значение момента инерции грузов Iг* и округлите его до той же значащей цифры, что и Iг.

9. Окончательные результаты выполнения лабораторной работы представьте в виде:

 
 


Iг =IгСР ± DIг,

Iг* =……

 

 

Контрольные вопросы

1. Какое свойство тела выражает момент инерции и как он вычисляется для материальной точки и системы матери­альных точек? В каких единицах он измеряется в СИ?

2. Объясните, из каких соображений в данной работе выбирается число значащих цифр после запятой при округлении результатов вычислений.

3. Выведите формулу (9); укажите возможные причины неко­торого несовпадения величин моментов инерции, определен­ных по этим формулам.

4. Сформулируйте основной закон динамики вращательного движения.

5. При каком положении грузов маховик Обербека раскручивается с наибольшим угловым ускорением? Ответ обоснуйте.

 

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

 

1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А. Гринчар, Ф.П. Денисов, Б.А. Курбатов и др.; Под общ. ред. Ф.П. Денисова. - М.: МИИТ, 1995. - 38 с.

 
 

 


РАБОТА № A4-П

ИЗМЕРЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО И ФИЗИЧЕСКОГО МАЯТНИКОВ

Цель работы: измерение ускорения свободного падения в поле сил тяжести.

Приборы и принадлежности: штатив универсальный, кронштейн, скоба, математический маятник (шарик диаметром 13 мм на нити), оборотный маятник, оптодатчик, линейка, измерительный блок L-микро.

 

Введение

 

Математическим маятникомназывается твёрдое тело, подвешенное на нити; массой нити можно пренебречь по сравнению с массой тела; размерами тела можно пренебречь по сравнению с размерами нити; по сравнению с размерами нити можно пренебречь и её возможным удлинением под действием внешних сил.В идеальном случае математическим маятником является материальная точка, подвешенная на невесомой и нерастяжимой нити. Можно показать, что если углы отклонения j такого маятника от вертикали малы (так, что j » tg j » sin j), то период Tмколебаний (время, за которое совершается одно полное колебание) описывается формулой

Тм= 2p . (1)

 

Здесь l – длина нити, g – ускорение свободного падения. (При выводе данной формулы предполагается, что на маятник не действует никаких других сил, кроме силы тяжести).
Физическим маятником называется абсолютно твёрдое тело, совершающее колебания относительно оси, проходящей через точку, не являющуюся центром тяжести тела. В механике под абсолютно твёрдым понимают тело, которое невозможно деформировать (реально – возможные деформации которого много меньше размеров тела). Если углы отклонения j такого маятника от вертикали малы (то есть j » tg j » sin j), то период Tфего колебаний рассчитывается следующим образом:

Тф= 2p . (2)

В этой формуле I – момент инерции маятника относительно оси, относительно которой происходят колебания, m – масса маятника, d – расстояние от центра его тяжести до этой оси.

Напомним, что момент инерции тела I относительно некоторой оси является мерой инертности тела при вращении его вокруг этой оси. Для материальной точки момент инерции равен произведению ее массы на квадрат расстояния до оси вращения:

I = mr2,

а для тела, которое можно представить в виде системы боль­шого количества материальных точек, момент инерции отно­сительно некоторой оси равен сумме произведений масс всех материальных точек на квадраты их расстояний до этой оси:

I = или I = .

Момент инерции зависит как от общей массы тела, так и от его формы, от характера распределения массы по объёму.

Как следует из формул (1) и (2), периоды колебаний математического и физического маятника зависят от ускорения свободного падения: измерив Тм или Тф в эксперименте, с учётом известных значений параметров маятника, можно вычислить, чему равно g.

Если измерение ускорения свободного падения с помощью математического маятника достаточно просто осуществить (и период колебаний и длина маятника легко измеряются):

g = 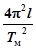, (3)
то проводить измерения g с помощью произвольного физического маятника уже не так просто. Дело в том, что для этого необходимо знать точное значение момента инерции маятника относительно выбранной оси и положение его центра масс (для измерения расстояния d). Поэтому для определения g используется прибор, называемый оборотным маятником, при использовании которого задача определения ускорения свободного падения сводится к измерению периода колебаний и некоторого расстояния между элементами конструкции такого маятника.

Оборотный маятник рис. 1 является физическим маятником, кото­рый устроен следующим образом. На стержне (1) закрепляются два груза (2), (3). Стержень имеет две оси вращения, расположенные, по разные стороны от центра масс (точка О)системы. Осями вращения служат рёбра вершин треугольных призм (4), (5), изготовленных из твердого материала; призмы установлены на специальную опору (6) закрепленную на подставке.

Оборотный маятник регулируется таким образом, чтобы период его колебаний при установке на одной призме равнялся периоду колебаний его на другой призме. Регулировка произ­водится путем изменения взаимного расположения грузов и призм на стержне.

Выведем формулу периода колебаний оборотного маятника. Согласно теореме Штейнера момент инерции I тела относительно произвольной оси равен сумме момента инерции I0 этого тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения его массы т на квадрат расстояния d между осями:

I = I0 + md2. (4)

После подстановки в формулу (2) получим:

Тф= 2p . (5)

Поскольку оборотной маятника имеет равные периоды колебаний на обоих призмах (осях), на основании (5) можно записать:
Тф= 2p

Тф= 2p . (6)

Здесь d1 и d2 – расстояния от центра масс маятника до рёбер первой и второй призм соответственно; очевидно,что d1 + d2 = b (см. рис. 1).

Возведем правые и левые части формул (6) в квадрат и умножим на знаменатели правых частей:

Tф2mgd1 = 4p2(I0 + md12),

Tф2mgd2 = 4p2(I0 + md22)

Вычтем из первого равенства второе и сократим на m:

Tф2g(d1- d2) = 4p2(d12 - d22),

Оборотный маятник несимметричен, то есть d1¹ d2, или, другими словами, d1- d2 ¹ 0. Поэтому мы можем сократить и правую и левую части данного уравнения на разность (d1- d2), в результате чего получим:

Tф2g = 4p2(d1 + d2),

или, с учётом того, что d1 + d2 = b,

Тф= 2p . (7)

Из этого выражения следует формула для определения g :

g = (8)

Подчеркнем, что в случае d1= d2 (симметричное расположение осей колебаний относительно центра масс маятника), формулы (7) и (8) не являются справедливыми. Величина периода колебаний в этом случае зависит не только от bи g, но и от момента инерции маятника I0.

 

Порядок выполнения работы
В данной лабораторной работе с помощью оптодатчика измеряется промежуток време­ни между двумя ближайшими прохождениями груза маятника через положение равновесия, т.е. непосредственно измеряется половина периода колебаний

1. Для проведения опыта с математическим маятником соберите установку как показано на рис. 2. Штатив собирается с длинной вертикальной стойкой (1), к которой крепится кронштейн (2). На конце кронштейна гайкой (3) зажимается шайба, к которой привязана нить с шариком (4). Высота расположения кронштейна (2) подбирается такой, чтобы центр шарика находился на одной высоте с излучателем и приемником оптодатчика (5). Оптическая ось датчика должна приблизительно совпадать с положением равновесия маятника.

 

2. Подключите измерительный блок L-микро к разъему последовательного порта компьютера. После этого подсоедините его к сети (220 В, 50 Гц) и включите. Оптодатчик подключается к первому каналу измерительного блока (рис. 3).

3. Запустите программу L-рhys.ехе, выберите пункт «СПИСОК ОПЫТОВ» и в появившемся на экране списке выберите лабораторную работу «Определение ускорения свободного падения».

4. При проведении опытов (как с математическим, так и с оборотным маятниками) необходимо привести маятник в движение и выбрать пункт меню «ИЗМЕРЕНИЕ». После совершения маятником пяти полных колебаний автоматическая запись данных прекращается, а на экране остаётся таблица полупериодов колебаний. Возможная разница между полупериодами Т0,5 и Т0,5¢, измеренными при движении маятника в одну и другую стороны, объясняется тем, что оптическая ось датчика не точно совпадает с положением равновесия маятника.

5. Измерьте период малых колебаний математического маятника. Для этого проведите измерения подупериодов при двух различных амплитудах колебаний, достаточно малых с тем, чтобы период не зависел от амплитуды (в рамках точности измери­тельной системы). Измеренные значения Т0,5 и Т0,5¢ колебаний внесите в таблицу 1; туда же запишите рассчитанные значения периодов колебаний маятника.

Измерьте линейкой расстояние l от центра шарика до точки подвеса и впишите полученное значение в таблицу 1.

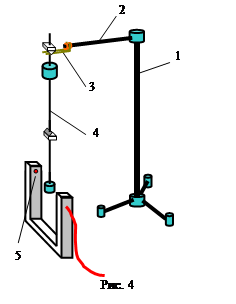6. Положите маятник горизонтально на какой-либо острый предмет (например, ребро линейки) и найдите приблизительно положение центра масс - точку, опираясь на которую маятник будет в равновесии. Проверьте, выполняется ли условие d1¹ d2 применимости формулы (8).
7. Для проведения измерений с оборотным маятником на конце кронштейна (1) с помощью двух гаек (2) закрепляется скоба (3) (рис. 4). Оборотный маятник (4) вставляется в прорезь скобы таким образом, чтобы плоскость его колебаний совпадала с направлением прорези. При движении маятник должен перекрывать луч света в оптодатчике (5), установленном на столе. Необходимо, чтобы оптическая ось датчика примерно совпадала с положением равновесия маятника. Высота расположения оси маятника регулируется перемещением кронштейна (2) по вертикальной стойке штатива (1).

 

Таблица 1

№ опыта Полупериод Т0,5, с Полупериод Т0,5¢, с Период Т, с Среднее значение периода ТСР, с Ошибка D Т измерения периода, с
1.          
     
     
     
     
2.          
     
     
     
     
Длина маятника l, м:

 

Таблица 2

№ опыта Полупериод Т0,5, с Полупериод Т0,5¢, с Период Т, с Среднее значение периода ТСР, с Ошибка DТ измерения периода, с
Призма 1 1.          
     
     
     
     
2.          
     
     
     
     
Призма 2 1.          
     
     
     
     
2.          
     
     
     
     
Расстояние между вершинами призм b, м:

 
8. Определите амплитуды колебаний, при которой их еще можно считать малыми, то есть найдите область амплитуд колебаний, где в рамках точности эксперимента период оборотного маятника не зависит от амплитуды. После этого установите маятник на одну из опор и (аналогично случаю математического маятника) проведите измерение периодов при двух амплитудах колебаний около одной призмы и затем, перевернув маятник, – при двух амплитудах колебаний около другой призмы. Результаты измерений запишите в таблицу 2. Измерьте линейкой расстояние b между остриями опор маятника d и также впишите его в таблицу 28. Положите маятник горизонтально на какой-либо острый предмет (например, ребро линейки) и найдите приблизительно положение центра масс - точку, опираясь на которую маятник будет в равновесии. Проверьте, выполняется ли условие d1¹ d2 применимости формулы (8).

9. На основе данных, полученных для матема­тического и физического маятников, вычислите значения ускорения свободного падения. Результаты запишите в таблицу 3.

 

Таблица 3

Математический маятник Физический маятник
Амплитуда 1 Амплитуда 2 Призма 1 Призма 2
Амплитуда 1 Амплитуда 2 Амплитуда 1 Амплитуда 2
gм1, м/с2 gм2, м/с2 gф1, м/с2 gф2, м/с2 gф3, м/с2 gф4, м/с2
           
Округлённые значения ускорения свободного падения
gм1*, м/с2 gм2*, м/с2 gф1*, м/с2 gф2*, м/с2 gф3*, м/с2 gф4*, м/с2
           
             

 

9. Рассчитайте ошибки измерения ускорения свободного падения в обеих сериях экспериментов. Поскольку измерения ускорения свободного падения – косвенные, и преобладающей является ошибка измерения времени, фиксируемого оптодатчиками, соответствующие ошибки рассчитываются как среднеквадратичные.

Среднеквадратичная ошибка sfизмерения какого-либо параметра f = f(x, y, z…) в общем виде рассчитывается по формуле

 

 

sf = .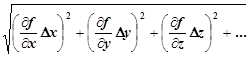

 
 


Для математического маятника g = 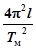, где Тм – средние значения периода (TСР из таблицы 1), следовательно,

 

sgм=

 

Продифференцировав это выражение по l иT, а также использовав, что Тм = TСР, после стандартных преобразований получаем необходимые формулы для расчёта sgм1и sgм2:

 

sgм1= (9)

 

В этой формуле Dl – приборная ошибка линейки для измерения l; DT1 = 0,0005 с – приборная ошибка измерения периода колебаний математического маятника при первом значении амплитуды колебаний (случайная ошибка определения периода мала).

Аналогично рассчитывается ошибка sgм2 для второго значения амплитуды колебаний математического маятника.

Для оборотного маятника g = , где Тф – средние значения периода (TСР из таблицы 2), следовательно,

 

sgф1= (10)

 

В этой формуле Db – приборная ошибка линейки для измерения b; DT1 = 0,0005 с – приборная ошибка измерения периода колебаний оборотного маятника при первом значении амплитуды колебаний.
Таким же образом рассчитывается ошибка sgф2измерения ускорения свободного падения при втором значении амплитуды колебаний оборотного маятника на той же призме, после чего вычисляются ошибки sgф3 иsgф4измерения g для двух амплитуд оборотного маятника, колеблющегося на другой призме.

10. Округлите полученные ошибки до первой значащей цифры; до этого же разряда округлите полученные ранее значения ускорения свободного падения и внесите эти значения в таблицу 3.

Итоговые результаты измерений представьте в виде:

 

 
 
gм1= gм1* ± s gм1 gм2= gм2* ± sgм2 gф1= gф1* ± sgф1 gф2 = gф2* ± sgф2 gф3= gф3* ± sgф3 gф4= gф4* ± sgф4    

 

 


.

 

Приступая к работе, помните:

- включать в сеть измерительный блок L-микро можно только после его подключения к разъему последовательного порта компьютера;

- с оборотным маятником следует обращаться осторожно: не допускайте падений и ударов ма­ятника, это может нарушить его юстировку.

 

Контрольные вопросы

1. Какой маятник называется математическим? В каком случае этот маятник совершает колебания с периодом, рассчитываемым по формуле (1)?

2. Какой маятник называется физическим? В каком случае этот маятник совершает колебания с периодом, рассчитываемым по формуле (2)?
3. Сформулируйте теорему Штейнера. Как эта теорема используется в настоящей работе?

4. Можно ли определить ускорение свободного падения, если у оборотного маятника расстояния от центра масс до обеих призм одинаковы? Ответ обоснуйте.

5. Выведите формулу для расчёта ускорения свободного падения с помощью оборотного маятника.

 

 

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

 

1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А. Гринчар, Ф.П. Денисов, Б.А. Курбатов и др.; Под общ. ред. Ф.П. Денисова. - М.: МИИТ, 1995. - 38 с.

 

       
 
 

 


РАБОТА № 5-П

ИЗУЧЕНИЕ ЗАКОНА СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

Цель работы: изучение динамики вращательного движения и закона сохранения момента импульса на примере системы с изменяющимся моментом инерции.

Приборы и принадлежности: штатив универсальный, датчик числа оборотов; стержни (спицы длинные) – 2 шт.; грузы – 2 шт.; ограничители хода грузов – 2 шт.; устройство для раскрутки системы; линейка; измерительный блок L-микро.

 

 

Введение

 

В механике важнейшими физическими закономерностями, описывающими поведение изолированных* систем, являются законы сохранения (см., например, учебники [1,2]) энергии, импульса и момента импульса. Наряду с законом сохранения электрического заряда эти законы обладают всеобщностью, в отличие от других законов сохранения (играющих, например, большую роль в квантовой теории и в теории элементарных частиц), справедливых лишь для определённых классов систем и явлений.

Приведём формулировку законов сохранения, используемых в механике.

1.Закон сохранения энергии: В изолированной системе, в которой действуют лишь консервативные** силы, полная механическая энергия системы остаётся постоянной величиной.

2. Закон сохранения импульса: Суммарный импульс изолированной (замкнутой) системы не меняется со временем:

= const. (1)

 

3. Закон сохранения момента импульса: Момент импульса замкнутой* системы материальных точек не зависит от времени:

 

= const.

 

Напомним, что моментом импульса материальной точки, обладающей импульсом , относительно некоторой точки O, связанной с ней радиус-вектором (вектор направлен от O к материальной точке), называется векторное произведение

 

= . (2)

Момент импульса тела (системы материальных точек) относительно некоторой точки O рассчитывается как векторная сумма моментов импульсов этих точек относительно точки O:

= = . (3)

Выражение (3) можно преобразовать, приняв во внимание, что

= mi ,

и что линейная скорость точки при вращении относительно оси, проходящей через выбранную точку О, связана с угловой скоростью соотношением

,

где - радиус вектор, проведённый от О до вращающейся точки. Это означает следующее:

= = = =

= = .

В случае абсолютно твёрдого тела (расстояние между отдельными точками которого не меняется со временем) при повороте относительно любой оси все точки поворачиваются относительно этой же оси на одинаковый угол, то есть угловые скорости всех точек твёрдого тела одинаковы: . Следовательно,

= = = .

Известно, что моментом инерции тела относительно выбранной оси называется выражение вида

I = . (4)

Следовательно, момент импульса твёрдого тела может быть представлен в виде:

= I . (5)

Таким образом, в соответствии с законом сохранения момента импульса для твёрдого тела, на которое не действуют внешние моменты сил, должно выполняться условие

I = const: (6)

произведение момента инерции относительно неподвижной оси на угловую скорость относительно этой оси есть величина постоянная для механических систем, на которые не действуют моменты внешних сил или в которых главный момент внешних сил относительно оси вращения равен нулю. Экспериментальной проверке этого соотношения и посвящена данная лабораторная работа.
Механическая система с переменным моментом инерции схематически показана на рис. 1. Длинный тонкий стержень может вращаться в горизонтальной плоскости, вокруг вертикальной оси, проходящей через его центр. На стержне имеется два груза, которые свободно скользят по нему. С помощью специального приспособления стержень приводится во вращение при минимальном удалении грузов от оси. После освобождения грузов они скользят по стержню до установленных заранее упоров. Момент инерции I системы при этом возрастает, а вращение замедляется.

Угловая скорость системы контролируется компьютерной измерительной системой; измерение геометрических характеристик дает возможность определить начальное и конечное значения момента инерции. Таким образом, можно рассчитать моменты импульса данной системы в начальном состоянии (при максимальной скорости вращения) и в конечном состояниях (после разлета грузов) и затем, сравнив их, убедиться в справедливости закона сохранения момента импульса.

 

Порядок выполнения работы

1. Соберите установку как показано на рис. 2. Для этого возьмите штатив с короткой вертикальной стойкой (1) и установите на него датчик числа оборотов (2). В муфту (3), установленную на оси датчика, вверните два тонких стержня (4) и наденьте на них грузы (5). Для ограничения перемещения грузов по стержням на них устанавливаются резиновые шайбы (6). Раскрутка грузов производится специальной рукояткой (7), которая одновременно фиксирует начальное положение грузов. Устройство для раскрутки надевается на муфту датчика числа оборотов.

2. Подключите измерительный блок L-микро к разъему последовательного порта компьютера и к сети (220 В, 50 Гц). Кабель датчика угловой скорости включите в разъем первого канала измерительного блока (рис. 3). Включите тумблер питания измерительного блока.

3. Вызовите программуL-рhуs.ехе, выберите пункт«СПИСОК ОПЫТОВ» и в появившемся на экране списке выберите лабораторную работу«Закон сохранения момента импульса.»
4. Приступите к выполнению опыта. Для этого необходимо:

а) Зафиксируйте положение грузов (5) с помощью устройства для раскрутки (7), установленного на муфту датчика. С помощью линейки измерьте расстояние r1 от оси вращения до центров масс грузов и внесите его в таблицу 1. Туда же запишите значения массы грузов m1 и m2(выгравированы на их поверхности). В этой же таблице приведены значения других параметров грузов: их высота Н, а также внешний (R1) и внутренний (R2) радиусы.

б) Установите резиновые ограничительные шайбы (6) на одинаковом расстоянии от центра вращения системы.

в) Включите режим регистрации данных компьютером. Для этого выберите пункт меню «запуск» (Отметим, что запись данных осуществляется в течение 20 секунд с момента выбора пункта меню).

г) Раскрутите систему грузов с помощью специального устройства (7) и резко поднимите его вверх, чтобы позволить грузам сдвинуться до резиновых шайб, ограничивающих их движение по стержням (4). Добейтесь того, чтобы после разлёта грузы останавливались на одинаковом расстоянии r2от оси вращения, не застревая по дороге и не отскакивая от упоров.
д) После завершения записи данных на экране компьютера появится график зависимости угловой скорости вращения системы от времени. Вам следует определить w1 – значение угловой скорости до того как грузы начнут разлетаться и w2 – значение угловой скорости системы с грузами, переставшими скользить по спицам. Для этого с помощью компьютерной мыши подведите курсор (вертикальную черту) к соответствующим точкам графика и выпишите в таблицу 2. значения угловых скоростей (цифры в верхней части экрана).

 

Таблица 1

Н, м R1, м R2, м m1, кг m2, кг
0,019 0,014 0,003    

 

Начальной скоростью вращения системы следует считать максимальное значение угловой скорости. Участок возрастания угловой скорости на графике соответствует раскрутке системы, а участок, где угловая скорость убывает – разлету грузов, то есть – движению в отсутствие внешних сил. (Моментом сил трения пренебрегаем.)

 

Таблица 2

№ r1, м r2 , м w1, рад/с Dw1, рад/с w2, рад/с Dw2, рад/с I1+I2,кг×м2 I1¢+I2¢, кг×м2
               
   
   
           
   
   
           
   
   

Измерения необходимо провести при одинаковых начальных (r1) и трёх различных конечных положениях r2ограничительных резиновых шайб, каждый раз проводя по3 запуска системы (итого – 9 измерений).

5. Используя данные экспериментов (см. таблицу 1), вычислите значения совокупных моментов инерции грузов I1 + I2и I1¢ + I2¢соответственно до и после разлёта. Грузы можно считать однородными цилиндрами, вращающимися относительно оси, параллельной той, которая проходит через центр масс цилиндра перпендикулярно его оси симметрии.

При расчётах следует применить теорему Штейнера: момент инерции тела I относительно произвольной оси равен сумме момента инерции I0 относительно оси, парал­лельной данной и проходящей через центр масс тела, и произведения массы тела т на квадрат расстояния d между осями:

 

I = I0 + md2. (7)

 

В нашем случае расстояния между осями OO¢и АА¢(или ВВ¢) – см. рис. 1, – OO¢и СС¢,OO¢и DD¢,равны r1, и r2 соответственно, причём момент инерции Iгруза – полого цилиндра с внешним радиусом R1, внутренним радиусом R2, высотой Н и массой m относительно оси АА¢рассчитывается по формуле:

I = (3R12 + 3R22 + H2). (8)

 

Значения m, R1 , R2 и Н возьмите из таблицы 1.

Таким образом, момент инерции грузов до разлёта вычисляется по формуле

I1 + I2 = (m1+ m2)[ (3R12 + 3R22 + H2) + r12], (9)

 

а после разлёта – по формуле

I1 ¢+ I2¢ = (m1+ m2)[ (3R12 + 3R22 + H2) + r22]. (10)

Результаты расчётов запишите в таблицу 2.
6. Учтём теперь, что момент инерции стержней, по которым скользят грузы, и находящейся на оси датчика угловой скорости муфты, к которой эти стержни крепятся, по величине сопоставим с моментом инерции подвижных грузов, и поэтому его необходимо учитывать при обработке данных эксперимента. Момент инерции IП подвижной (без грузов) части установки следует вычислить, исходя из теоретических соображений. Значение момента инерции муфты IМ и её радиуса RМприведено в таблице 3; момент инерции стержней – цилиндров длиной l, массой m0 (также см. таблицу 3) может быть рассчитан следующим образом.

 

Таблица 3

IМ, кг×м2 RМ, м l, м т0, кг IС , кг×м2 IП, кг×м2
0,000002 0,0125 0,160 0,032    

 

Момент инерции спицы – тонкого однородного стержня относительно оси, проходящей через центр масс стержня перпендикулярно стержню, рассчитывается по формуле

 

I = m0l2 . (11)

 

 

В нашем случае спицы вращаются относительно другой оси - ОО¢, которая сдвинута от той, для которой получена формула (9), на расстояние

d = RМ+ .

 

Расчёт момента инерции относительно этой оси можно выполнить с помощью теорема Штейнера:

 

IС = m0l2 + m0 , (12)

 

и, следовательно, – вычислить момент инерции IП всей подвижной части без грузов: муфты и двух спиц:

 

IП = IМ + 2 . (13)

 

Результаты вычислений запишите в таблицу 3.
При расчётах IС и IП следует сохранять столько же знаков после запятой, сколько их содержит IМ.

7. Пользуясь формулой (5), а также данными таблиц 2 и 3, рассчитайте значения моментов импульса Liсистемы (включающей в себя муфту, спицы и грузы) до разлёта грузов и Li¢ -после их разлёта. Результаты запишите в таблицу 4.

 

 

Таблица 4

№ средние
L, кг×м2×с- 1                    
L¢, кг×м2×с- 1                    

 

 

Пример расчёта момента импульса Liдо разлёта грузов:

 

Li = [I1+I2+IП]w1i.

 

 

Пример расчёта момента импульса Li¢системыпосле разлёта грузов:

Li¢ = [I1¢+I2¢+IП]w2i.

 

Сопоставьте значения моментов импульса до и после разлета грузов и проанализируйте причины, которые приводят к некоторым отличиям в полученных результатах.

ВНИМАНИЕ:

1. Включать в сеть измерительный блок L-микро можно только послеего подключения к разъему последовательного порта компьютера.

2. Перед раскруткой системы убедитесь в правильной установке ограничителей хода грузов.

 

Контрольные вопросы

1. Что называется моментом импульса тела относительно некоторой точки? Как выглядит соответствующая формула в случае абсолютно твёрдого тела?

2. Сформулируйте закон сохранения момента импульса. Приведите пример проявления этого закона на практике.

3. Сформулируйте теорему Штейнера и приведите примеры её применения для расчётов в настоящей лабораторной работе.
4. Выведите формулу (13 ) момента импульса подвижной части системы.

5. Проанализировав результаты проведённых измерений, объясните, что является основным источником погрешностей в определении момента импульса системы.

 

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

 

1. Савельев И. В. Курс общей физики: В 3-х т. – М.: Наука, 1987. – Т. 1, 432 с.

2. Яворский Б.М., Детлаф А.А. Курс физики. – М.: Высш. шк., 2000.

3. Расчет погрешностей в лабораторных работах физического практикума. Методические указания к вводным занятиям в физическом практикуме/ Н.А. Гринчар, Ф.П. Денисов, Б.А. Курбатов и др.; Под общ. ред. Ф.П. Денисова. - М.: МИИТ, 1995. - 38 с.

 

 


РАБОТА № 6-П