ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ НА МАХОВИКЕ ОБЕРБЕКА
Цель работы: Измерение момента инерциитвердых тел, исследование зависимости момента инерции от формы тела.
Приборы и принадлежности: маховик Обербека, набор грузов, штатив универсальный, линейка, штангенциркуль, датчик угловой скорости с муфтой, измерительный блок L-микро.
Введение
В лабораторной работе рассматривается вращательное движение устройства, которое исторически получило название маховика Обербека.
Для описания вращательного движения, как и для описания поступательного движения, используется ряд параметров, определения некоторых из которых приведены в таблице 1
Таблица 1
| ПАРАМЕТРЫ, ХАРАКТЕРИЗУЮЩИЕ ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ПО ПРЯМОЙ | ПАРАМЕТРЫ, ХАРАКТЕРИЗУЮЩИЕ ПЛОСКОЕ ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ |
D  - перемещение
(x - координата) - перемещение
(x - координата)
|  - угол поворота
j- величина угла поворота - угол поворота
j- величина угла поворота
|
 - скорость; - скорость; 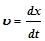
|  - угловая скорость; - угловая скорость; 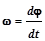
|

| |
 - ускорение; - ускорение; 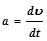
|  - угловое ускорение; - угловое ускорение; 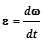
|

| |
 - импульс - импульс
|  - момент импульса отн. точки; L = r×p×sin a - момент импульса отн. точки; L = r×p×sin a
|
 - сила - сила
|  = =  - момент силы отн. точки;
M = r×F×sin a - момент силы отн. точки;
M = r×F×sin a
|
| M - масса | I = Smi ri2 – момент инерции |
| |
Сходным образом записываются и формулы основных законов, поступательного и вращательного движения (см. таблицу 2).
Таблица 2
| НЕКОТОРЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ, ОПИСЫВАЮЩИЕ ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ПО ПРЯМОЙ | НЕКОТОРЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ, ОПИСЫВАЮЩИЕ ПЛОСКОЕ ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ | ||||
| |u|=const - равномерное движение: х = х0 ±|u|t | w =const - равномерное вращение: j = j ±|w|t | ||||
движение: х = х0 ±|u0|t ± | e =const - равнопеременное
вращение:
j = j ±|w0 |t ±  w=±|w0|±|e|t w=±|w0|±|e|t
| ||||
Второй закон Ньютона
(основной закон динамики):
 - в общем случае;
или - в общем случае;
или  - при m =const, где - при m =const, где  - равнодействующая всех сил, действующих на тело - равнодействующая всех сил, действующих на тело
| Основной закон динамики
вращательного движения:
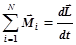 - в общем случае;
или - в общем случае;
или 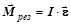 - для абсолютно твёрдого тела, где - для абсолютно твёрдого тела, где  - равнодействующий момент всех сил, действующих на тело - равнодействующий момент всех сил, действующих на тело
|
Из приведённых выше формул следует, в частности, что аналогом массы при вращательном движении является момент инерции I; определению I маховика Обербека при различных положениях грузов на спицах и посвящена настоящая работа.
Напомним, что момент инерции тела I относительно некоторой оси является мерой инертности тела при вращении его вокруг этой оси. Для материальной точки момент инерции равен произведению ее массы на квадрат расстояния до оси вращения:
I = mr2,
а для тела, которое можно представить в виде системы большого количества материальных точек (рис. 1.а), момент инерции относительно некоторой оси вращения равен сумме произведений масс всех материальных точек на квадраты их расстояний до этой оси:
| |
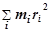 . (1)
. (1)

Для вычисления момента инерции сплошного тела его мысленно разбивают на бесконечное малые области с массами dm,каждая из которых находится на своём расстоянии r от оси вращения (рис. 1.б); I находят интегрированием по всем этим областям:
I = 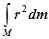 .
.
Понятно, что момент инерции зависит не только от общей массы тела, но и от формы тела, а также – от распределения массы по его объёму (так, например, какие-то части тела могут быть изготовлены из более тяжёлого материала, а какие-то – из более лёгкого).
Ось вращения может проходить через центр масс тела, а может и находиться вне его (рис. 1.в). Во втором случае для вычисления момента инерции пользуются теоремой Штейнера.
Момент инерции тела I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела т на квадрат расстояния d между осями:
I = I0 + md2. (2)
При конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т.д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.
| |

 При выполнении лабораторной работы Вам необходимо измерить момент инерции маятника Обербека в двух случаях: в отсутствие грузов на стержнях и при максимальном удалении грузов от оси вращения. В каждом случае раскрутка маятника проводится одним из двух перегрузков (6) – по выбору преподавателя.
При выполнении лабораторной работы Вам необходимо измерить момент инерции маятника Обербека в двух случаях: в отсутствие грузов на стержнях и при максимальном удалении грузов от оси вращения. В каждом случае раскрутка маятника проводится одним из двух перегрузков (6) – по выбору преподавателя.
Рассмотрим движение маятника Обербека, используя законы динамики. Перегрузок (6) массойтП на нити (5) движется поступательно с ускорением a под действием силы тяжести mПg и силы натяжения нити T. Можно записать уравнение второго закона Ньютона для этого груза:
mПg - T = mПa. (3)
Отсюда находим силу натяжения нити: Т= тП(g - а) и вычисляем момент M этой силы относительно оси вращения:
M = Tr = тП(g - а)r , (4)
где r – радиус цилиндрической поверхности-муфты, на которую намотана нить).
| |
тП(g - а)r = I·e, (5)
где e - угловое ускорение вращающегося маятника, причём а = er.
Эта формула может быть использована для определения момента инерции I1 крестовины с грузами:
I1= mП(g - e1r)r/e1 (6)
и без грузов:
I2= mП(g - e2r)r/e2. (7)
Момент инерции крестовины с грузами может быть также представлен в виде:
I1= I2 + Iг, (8)
где Iг – момент инерции четырёх грузов.
Таким образом, появляется возможность экспериментального определения момента инерции грузов на крестовине:
Iг = I1- I2 = mП(g - e1r)r/e1- mП(g - e2r)r/e2. (9)
Результаты вычислений по формуле (9) предлагается сравнить с теоретическим значением момента инерции грузов Iг*, рассчитываемым в предположении, что размерами грузов много меньше расстояния от их центра до оси вращения крестовины:
Iг* = m1R12+ m2R22 + m3R3 2 + m4R42, (10)
в которой m1,m2 ,m3иm4 – массы каждого из четырёх грузов, а R1,R2 , R3и R4 – расстояния от центров этих грузов до оси вращения.
Порядок выполнения работы
| |
Запишите значения масс грузов miв таблицу 3. Установите грузы на стержнях в непосредственной близости от концов стержней. Измерьте удаление Riкаждого из грузов от оси вращения и внесите полученные значения в ту же таблицу.
Закрепите один конец нити длиной 25 - 30 см на катушке муфты датчика угловой скорости и прикрепите к другому ее концу один из перегрузков (6). Перед запуском маятника Вам будет необходимо намотать нить на катушку муфты и таким образом поднять перегрузок над поверхностью стола.
 u =±|u0|±|а|t
u =±|u0|±|а|t