ЭНЕРГЕТИЧЕСКАЯ ДИАГРАММА ИДЕАЛЬНОГО ГЕТЕРОПЕРЕХОДА
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение
Высшего профессионального образования
«ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»
Факультет физико-математических и компьютерных наук
Кафедра физики
Специальность 050203.65 – «Физика и информатика»
Курсовая работа
по дисциплине (Физика)
на тему:
Гетероструктуры полупроводников
Выполнил:
студент 4 курса
группы ФИ-4
Корнев Денис
Липецк 2012
Содержание.
1. Определение гетероперехода.
2. Энергетическая диаграмма идеального гетероперехода.
3. Требования к материалам, образующим гетероструктуры.
4. Применение гетероструктур в наноэлектронике.
5. Приложение.
6. Использованная литература.
ОПРЕДЕЛЕНИЕ ГЕТЕРОПЕРЕХОДА
Полупроводниковые гетероструктуры лежат в основе конструкций современных транзисторов , приборов квантовой электроники, СВЧ - техники , электронной техники для систем связи, телекоммуникаций, вычислительных систем и светотехники.
Основным элементом гетероструктур различного типа является гетеропереход.
Под гетеропереходом понимается контакт двух различных по химическому составу полупроводников , при котором кристаллическая решетка одного материала без нарушения периодичности переходит в решетку другого материала.
Различают изотипные и анизотипные гетеропереходы . Если гетеропереход образован двумя полупроводниками одного типа проводимости, то говорят об изотипном гетеропереходе . Анизотипные гетеропереходы образуются полупроводниками с разным типом проводимости.
Существует три модели гетероперехода :
- идеальный гетеропереход;
- неидеальный гетеропереход;
- гетеропереход с промежуточным слоем .
В идеальном гетеропереходе , в отличие от неидеального , на границе раздела материалов отсутствуют локальные энергетические состояния для электронов . Гетеропереход с промежуточным слоем формируется через слой конечной толщины и локальные энергетические состояния могут существовать как в самом промежуточном слое , так и на границах его раздела.
ЭНЕРГЕТИЧЕСКАЯ ДИАГРАММА ИДЕАЛЬНОГО ГЕТЕРОПЕРЕХОДА
Для построения энергетической диаграммы часто применяют простое « правило электронного сродства » ( в англоязычной литературе – правило Андерсона), согласно которому разрыв зоны проводимости равен разности электронного сродства двух материалов . Но следует иметь в виду, что данный подход далеко не всегда справедлив , так как в разрыв зон зависят еще и от деталей формирования связей на гетерогранице и деформационного потенциала .
Для построения энергетической диаграммы идеального гетероперехода должны быть известны следующие характеристики полупроводников :
- ширина запрещенной зоны ( 
, 
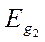). При построении считаем, что 
;
- термодинамическая работа выхода ( 
, 
)– расстояние от уровня Ферми полупроводника до уровня вакуума . Следует учитывать, что термодинамическая работа выхода зависит от положения уровня Ферми , то есть от уровня легирования материала;
- сродство к электрону ( 
, 
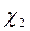) – расстояние от дна зоны проводимости до уровня вакуума .
При построении диаграммы считаем, что
- ширина запрещенной зоны и внешняя работа выхода неизменны до плоскости контакта , на которой они скачком изменяют свою величину;
- в приконтактном слое каждого из полупроводников происходит изменение потенциальной энергии электрона. Полное изменение потенциальной энергии равно разности работ выхода, что обеспечивает неизменное положение уровня Ферми вдоль гетероперехода .
До «приведения в контакт» двух полупроводников потенциальная энергия электронов в них разная из - за разной термодинамической работы выхода. При «соприкосновении » двух полупроводников , как и в случае обычного p-n-перехода , электроны начнут « переходить » из полупроводника с меньшей работой выхода в полупроводник с большей . Это будет происходить до тех пор , пока диффузионный ток не будет скомпенсирован дрейфовым током носителей заряда под воздействием поля , созданным избыточными носителями. При этом возникнет контактная разность потенциалов
и образуется область пространственного заряда шириной d (Рисунок 1 ).
Рисунок 1. Энергетические диаграммы полупроводников (а ) и диаграмма идеального гетероперехода ( б).
При таком построении видно , что из -за различия электронного сродства в контактирующих полупроводниках дно зоны проводимости первого полупроводника выходит на плоскость контакта в точке, не совпадающей в общем случае с точкой выхода на эту плоскость дна зоны проводимости второго полупроводника – формируется разрыв зоны проводимости 
. Он равен
Аналогично формируется и разрыв валентной зоны. Он равен:
Следует заметить , что разрывы зон могут быть как положительными так и отрицательными. Можно выделить следующие разновидности гетеропереходов:
1) охватывающий переход возникает, когда разрыв зоны проводимости 
и разрыв валентной зоны 
положительны. Такой случай реализуется, например, в гетеропереходе GaAs-AlGaAs. В литературе данный тип гетероперехода называют гетеропереходом I типа , или стандартным;
2) в случае же, когда разрыв один из разрывов зон положителен, а другой отрицателен говорят о переходе II типа, или ступенчатом. Данный случай реализуется в гетеропереходе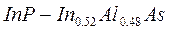 
.
3) также возможен вариант, когда запрещенные зоны вообще не перекрываются по энергии. Данный гетеропереход называет гетеропереходом III типа или разрывным гетеропереходом. Классический пример – гетеропереход InAs-GaSb. Экспериментально измеренные параметры основных типов гетеропереходов изображены на рисунке 2.
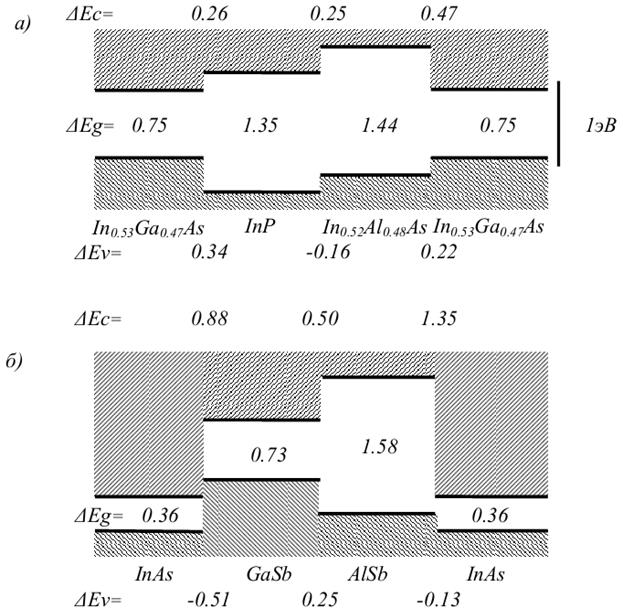
Рисунок 2. Экспериментально определенные разрывы валентной зоны и зоны проводимости двух наиболее близких по параметрам решетки гетеропар:а) 
и б ) InAs-GaSb-AlSb.
В справочниках обычно приведены величины эффективных масс плотности состояний для электронов 
и дырок 
. Тогда 
и 
вычисляются по формулам
, 
Если приведены поперечная 
и продольная 
составляющая эффективных масс , число эквивалентных эллипсоидов M, то плотность состояний в этом случае рассчитывается по формуле
В полупроводниках p-типа необходимо также учесть вклад двух подзон от легких и тяжелых дырок :
Далее по формулам вычисляем положение уровня Ферми и контактную разность потенциалов:
.
Для вычисления распределения потенциала в области пространственного заряда требуется решить совместно уравнение Пуассона и уравнение плотности тока , при условии, чтобы в равновесии диффузионный ток через переход уравновешивался дрейфовым током .
В приближении Шоттки в случае равномерного легирования полупроводников для анизотипного гетероперехода получается линейная зависимость поля и параболическая зависимость потенциала :
в области 
В области 
А размер области пространственного заряда получаются равными :
где 
, 
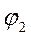– контактные разности потенциалов, приходящиеся на n и p области,которые для идеального гетероперехода равны :
, 
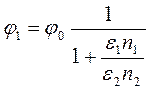Полная длина ОПЗ :
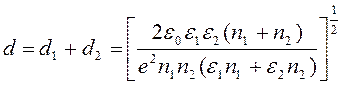
Распределение поля и потенциала показано на рисунке 3.
Рисунок 3. Распределение поля и потенциала в резком анизотипном гетеропереходе.
Следует также принимать во внимание, что материалы гетеропары могут иметь минимумы зоны проводимости в разных точках зоны Брюллиена . К примеру , минимум зоны проводимости GaAs находится в точке Г, в то время как наименьший минимум в AlAs близок к точке X. Таким образом, природа низшего минимума зоны проводимости меняется при изменении доли Al в твердом растворе 
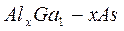(рисунок 4). Низший минимум 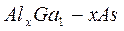изменяется от прямого расположения ( минимум в Г) зон до непрямой зонной структуры ( минимум в Х) при содержании 
. Обычно твердый раствор 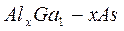получают с долей Al, меньше 0.4, чтобы получить прямое расположение зон.
Рисунок 4. Расположение валентной зоны и зоны проводимости в
.
Покажем простой способ построения энергетической диаграммы на конкретном примере . Пусть требуется построить энергетическую диаграмму 
. Используя справочные данные ( см. Таблица 1 ), находим ширину запрещенной зоны и электронное сродство для материалов гетеропары . При этом учитываем , что при х =0.3 минимум зоны проводимости твердого раствора 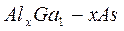лежит в точке Г ( см. рисунок 4). Для GaAs получаем 
и 
χ1=4.07 эВ, а для 
– 
и 
.
Построение зонной диаграммы разобьем на несколько этапов . Сначала отдельно нарисуем зонные диаграммы для GaAs и 
в отсутствие контакта . Относительно энергии электрона в вакууме их следует располагать, используя определение электронного сродства .
Сразу можно вычислить разрыв зон проводимости. Разрыв зоны проводимости:
и разрыв валентной зоны:
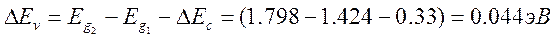
В данном случае , 
, таким образом, этот гетеропереход относится к гетеропереходу I типа - дно зоны проводимости лежит выше дна зоны проводимости GaAs, а потолок валентной зоны лежит ниже потолка валентной зоны GaAs (рисунок 5, а).
Далее нарисуем уровни Ферми в двух полупроводниках в соответствии с уровнем легирования (рисунок 5, б ). В данном примере считаем полупроводники невырожденными и просто располагаем уровень ферми в GaAs ближе к потолку валентной зоны, а в – ближе к дну зоны проводимости. Проводим ряд вспомогательных линий , которые помогутправильно построить диаграмму : это уровни 
, 
, являющиеся продолжением 
, 
GaAs в 
(рисунок 5, б ).
Соединим плавной пунктирной линией уровни , и , в GaAs ( рисунок 5, в). На последнем этапе нарисуем разрывы зон (рисунок 5, г).
Рисунок 5. Пример построения энергетической диаграммы гетероперехода
p-GaAs-n-AlGaAs .