Лекция №2

 

1.2. Қиықтау әдісі

Бұл әдіс бір немесе бірнеше алдыңғы сандарды бейсызықты түрлендіру нәтижесінде табылған жаңа санның цифрларының бір бөлігін алып тастау, немесе қию жолымен алынған кезекті кездейсоқ сандарды табуға негізделген.

Қиықтау әдісінің идеясын қолданып, бірқалыпты үлестірімді кездейсоқ сандарды тудыратын алғашқы алгоритмді 1946 жылы Фон Нейман мен Метрополис ұсынған болатын. Бұл алгоритм "орта шаршы" деген атқа ие болды, және 2k – орынды сандармен жұмыс істейді. Есептеу алгоритмі келесі қадамдардан тұрады:

1-қадам. деп адамыз.

2-қадам. 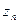-ді шаршылаймыз: -қадам. Алынған шаршының орта цифрын алып, оларды тізбектің келесі санының разрядтары деп есептейміз:

Бұл алгоритм, бізге бұрыннан белгілі, (1.2) формуласына сәйкес келетініне оңай көз жеткізуге болады.

1.1. мысал, болсын, сонда к = 2 болады. Шешімі:

=0,1981 =0,03924361

= 0,9243 = 0,85433049

= 0,4330 =0,18748900
= 0,7489 және т. б.

Өкінішке орай, орта шаршы алгоритмі көп жағдайларда статистикалық канағатты нәтижелер бермейді. Осы алгоритммен тізбектелген кездейсоқ сандардың арасында мәні кішірек, яғни сандар көбірек кездеседі. Сонымен қатар, тізбектің аяғы нольге айналуын, яғни тізбектің жұпындалуын жиі байқауға болады.

50-ші жылдардың бас кезінде американдық ғалым Дж. Форсайт жүргізген сынақтар мынандай нәтижелер берді. 16 бастапқы мәндердің 12-сі;

0,6100; 0,2100; 0,4100; 0,8100; 0,6100

циклмен аяқталатын тізбекке, ал екеуі тізбектің жұпындалуына алып келді.

Кейде орта шаршы алгоритммен жасалған тізбекте кездейсоқ сандар тіпті байқалмайды.

1.2. мысал [3] z₀ =0,4500 тең болсын. Шешімі:

= 0,4500 = 0,20250000

= 0,2500 = 0,06250000

= 0,2500 = 0,06250000

= 0,2500 және т. б.

Осы кемшіліктердің салдарынан қазіргі уақытта орта шаршы алгоритмі кең колданылмайды және ол біз үшін тек тарихи көзқарас түрінде қалады. Оның бұрынғы кең қолданылуы қарапайымдылығы мен қызық ерекшелігі арқылы түсіндіріледі.

Дж. Фон Нейманның жолын қуушылар бұл алгоритмнің біраз модификациясын ұсынды. Мысалы, жақсы нәтижелерге

(1.3)

функциясына негізделген алгоритммен жетуте болады. Соған қарамастан, қазіргі кезде кездейсоқ сандар тізбегін тудыратын барлық қолданбалы программалар шегерінділер мен қосындылар әдістеріне негізделген.

1.3. Шегерінділер әдісі (конгруэнттік әдіс)

Бұл әдісті 1948 жылы Д.Леймер ұсынған болатын. Жалпы жағдайда шегерінді әдісі мына түрдегі сызықты формулаға негізделеді:

(1.4)

Мұндағы ,a,c және т - теріс емес бүтін сандар.

(1.4) түріндегі жазу саны өрнегін т-ге бөлгендегі қалдыққа тең екенін көрсетеді, басқаша айтқанда, - бұл -ң т модулі бойынша алынған ең кіші оң шегеріндісі. Параметрлері қандай да мәнге ие болмасын (1.4) формуласымен тек қана ақырлы жиын құратын бүтін кездейсоқ сандар ғана алуға болады, содан кейін тізбектегі сандар қайталана бастайды. Бұл айқындығы күмәнсіз р<т шектелуінен келіп шығады, мұндағы р - кездейсоқ тізбектің периоды.

1.3. Мысал, a = 7, 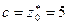, m = 9 болсын.

Сонда

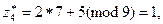
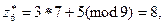
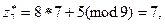
және т.б.

Енді (1,4) өрнегінің с = о болған жағдайдағы дербес түрін қарастырайық:

(1.5)

Бұл формула кездейсоқ тізбектерді біршама тез, бірақ (1.4) формуласына қарағанда азырақ периодпен модельдейді.

1.4. мысал а, т, параметрлерінің мәндерін бұрынғыдай қалдырамыз.

Сонда:

1.З.-мысал шегерінділер әдісінің бір артықшылығын жақсы бейнелейді. Ол (1.4) өрнегін қолданғанда кездейсоқ сандар тізбегінің ешқашан жұлыланбайтындығы. Сонымен бірге, бұл мысалдар (1.4) және (1.5) формулалардағы параметрлердің мәндерін ойламай таңдаса, яғни олардың орнына кез-келген цифрларды қоя салса, ешқашан жақсы статистикалық қасиеттері бар кездейсоқ сандар тізбектері алынбайтындығын көрсетеді. Сондықтан, а, с, т параметрлерін және кездейсоқ тізбектің бастапқы санын ( ) таңдағанда мынадай жағдайлар есте болуы керек: тізбектің периоды неғұрлым үлкен, тізбекті генерациялаудың жылдамдығы жоғары және кездейсоқ сандардың арасындағы корреляция неғұрлым кем болғаны жөн.

Қазіргі кезде компьютерде қолдануға шегерінділер әдісінің (1.5) формуласы ыңғайлы екені анықталған [4]. Ол үшін болуы қажет. Мұндағы b - машиналық сөздегі екілік цифрдың саны. Сонда кездейсоқ тізбектің р=т/4 тең болатын максималды периодына мына шарттар орындалғанда жетуге болады:

1). кез-келіен оң, так, бүтін сан;

2). , мүндағы t - кез-келген оң бүтін сан.

Ал енді шегерінділер әдісінің (1.4) формуласына келсек, онымен кездейсоқ сандар тізбегін модельдегенде периодтың ең максималды р=т мөлшеріне жетуге болады. Бұл нәтижені мына теорема дәлелдейді.

Теорема 1.1. (1.4) формула бойынша алынған кездейсоқ тізбек периодының ұзындығы т-ғa тең болу үшін мынадай шарттар орындалуы керек:

а) с және т - өзара жай сандар;

б) (а-1) саны r-ге еселі, егер r жәй сан және m санының бөлгіші
болса;

в) (а-1) саны 4-ке еселі, егер m саны төртке еселі болса.
Бұл теореманың дәлелдемесін [5] табуға болады.

Кездейсоқ тізбек периодының ұзындығы дәл m болғандықтан, 0 мен (m-1)-дің арасындағы әр сан бұл тізбекте бір ақ рет кездеседі, Сондықтан -ң мәні периодтың ұзындығына әсер етпейді. Айта кететін тағы да бір жәй (1.4) және (1.5) формулаларымен алынған кездейсоқ тізбектер мүшелерінің мәндері [о:т] кесіндісіне бірқалыпты орналасады, ал [0;1] аралығындағы сандарды алу үшін бүл формулаларды мьша өрнекпен толтыру қажет:

1.4. Қосындылау әдісі

Ван Вейнгарден ұсынған қосындылау әдісі мына жалпы мағыналы сызықтық формуланы қолданады [6]:

(1.7)

Бұл әдіспен алынған кездейсоқ тізбектердің периоды шегерінді әдісі қолданғандағы периодтан едәуір ұзын болады. Оның себебі, бұл тізбектерде период пайда болу үшін шегерінді әдісі сияқты оның екі ғана емес, бірнеше мүшесі сәйкес келуі керек. Сонымен қатар, қосындылау әдісімен алынған тізбек сандарының корреляциясы аз.

Қосындылау әдісінің ең қарапайым формуласын алу үщін (1.7) өрнегінің параметрлеріне мынадай мағына беру керек:

Сонда

Бұл өрнек Фибоначчи формуласы деген атқа ие болды және өткен ғасырдың елуінші жылдарының бас кезінде кең колданыс тапты. Алайда, Фибоначчи формуласымен генерацияланған сандар жеткілікті кездейсоқ болған жоқ. Тек қана Дэвис деген ғалым осы формуламен, оның бастапқы z₀ және , сандарын сәтті таңдап, статистикалық қасиеттері жақсы бірқалыпты кездейсоқ сандардың тізбегін алды.

Дэвистің алгоритмі [7] мына формуланы қолданады:

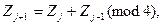(1.9)

мұндағы z₀ = π, .

Қазіргі уақытта қосындылау әдісі алгоритмдерінің арасында ең көп тарағаны аддитивті алгоритмдер болып отыр [8]. Ол алгоритмдер мына формуламен сипатталады:

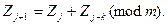
Мұндағы к - үлкен жэне бүтін сан (к ≥16).

Бастапқы 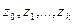сандарын ойлағандай таңдаған күнде, бұл алгоритмдер статистикалық қасиеттері жақсы кездейсоқ сандардың көзі бола алады.

1.5. Кездейсоқ тізбектердің периоды мен апериодтылығының ұзындылығын сынақ арқылы анықтау

Жоғарыда келтірілген деректерден анық көрінетін бір ерекшелікті қарастырайық. Ол ерекшеліктің мәіні мынада. Кездейсоқ сандар тудыратын әдістердің бәрі де, оларды компьютерде қолданғанда, периодикалық тізбек тудырады. Шынында, кез-келген компьютердің кодында [0;1] арадығында жататын әр түрлі сандардың тек шекті мөлшерін ғана жазуға болады, сондықтан ерте ме, кеш пе z_L санының мәні алдындағы сандардың мәндерінің біреуімен, мысалы -мен, сәйкес келеді. Онда келесі теңдік тура болады:

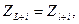
(1.10)

Сурет

L - (1.10) шартын қанағаттандыратын, ең кіші сан болсын. Сонда сандар жиыны кездейсоқ тізбектің апериодты кесіндісі деп аталады (1.3-сурет). Ал, L апериодтылық кесіндінің ұзындығы, (L-1) мәні периодқа тең екені 1.3-суреттен айкын көрінеді, яғни P=L-l. Сонымен, тізбек тек кездейсоқ сандардан тұруы үшін оның ұзындығы апериодтық кесіндінің ұзындығынан аспауы тиіс. Сондықтан L мен р-ң нақты мәндерін таба білу керек. L мен P-ң мәнін сынақ арқылы анықтаудың бір әдісіне тоқтайық [9, 10].

{ }- жоғарыда көрсетілген алторитмдердің біреуінің көмегімен алынған кездейсоқ сандар тізбегі болсын. Осы тізбектің индексі l-p айырымынан біраз үлкен мүшесіи жадымызда сақтап қаламыз (1.4.-сурет). Сонан соң -ді - сандарының біреуімен сәйкес келгенше салыстырамыз. Ерте ме, кеш пе, осы салыстырудың нәтижесінде мына тендікке жетеміз:

z_N = z_k (k> N).

Сурет

Демек, k-N=р тізбек периодының ұзындығы. Содан соң, берілтен алгоритммен мынандай екі кездейсоқ тізбекті қатар генерациялаймыз:

және осы тізбектердін, қатар алынған мүшелерін, олар бір-біріне

теңелгенше, яғни мына теңдеу:

орындалғанша салыстырамыз. Сонда (1.12) тізбегінің сәйкес келген мүшесінің номері апериодтылығының ұзындығын анықтайды. Айтылғандарды мынадай алгоритм түрінде келтірейік:

1-қадам. i= 1, R = о деп аламыз, мұндағы R - тізбек периодының ұзындығы әлі табылмағандығының белгісі.

2-қадам. Кездейсоқ тізбектің кезекті мүшесін генерациялау.

3-кадам. i = i +1 болсын.

4-қадам. R = о шартын тексеру. Бұл шарт орындалмаса 7-қадамды орындау керек.

5-қадам. i = N+1 шартын тексеріп, ол орындалмаған жағдайда 2-қадамға көшу керек.

6-қадам. Y= және r = r +1 деп алып, 2-қадамға көшу керек.

7-қадам. = ү шартын тексеріп, ол орындалмаған жағдайда 2-қадамға қайту керек.

8-қадам. Периодтың ұзындығын мына өрнектен P= і - N анықтап алып, і -ді бірге теңеу керек: і = 1.

9-қадам. Зерттеліп отырған кездейсоқ тізбектің және мүшелерінің мәндерін қайтадан табу керек.

10-қадам. = , шартын тексеріп, ол орындалған жағдайда, 12-қадамға көшу.

11-қадам. і = і + 1 деп алып, 9-қадамға қайтып бару.

12-қадам. Апериодтық кесіндінің ұзындығын мына өрнектен L = P + і айқындау.

13-қадам. р мен L –дің мағынасын компьютердің мониторына әлде принтерге шығару.

1.6. Қалыптан ауытқу әдісі

L мен р-ның мәндері өте үлкен бірқалыпты үлестірімді кездейсоқ сандардың тізбегін модельдеу үшін украин ғалымы Д.И.Голенко ұсынған қалыптан ауытқу әдісін қолдануға болады, Бұл әдістің идеясы бір кездейсоқ тізбекті модельдеу ушін қатарымен екі алгоритмді пайдалануға негізделген:

м параметрі м < l шартынан таңдалады және калыптан ауытқу периоды деп аталады.

(1.13) өрнегінен көрініп тұрғандай, жоғарғы Ф(z) функциясы көмегімен тізбегі модельденеді. Ал содан кейін

сәйкестелуін болдырмау үшін, z_M кездейсоқ саны төмендегі функциясының көмегімен табылады. Осындай ауытқу одан әрі де, келесі м – 1 кездейсоқ саннан асқан сайын, тізбектің берілген ұзындығына жеткенше қайталанып отырады.

Қалыптан ауытқу әдісін іске асыратын алгоритм 7 қадамнан тұрады.

1-қадам. K=1 және j = о деп аламыз.

2-қадам. j =K*M шартын тексереміз. Бұл шарт орындалған жағдайда 4-қадамға көшеміз.

3-қадам. рекурренттік қатынасын іске асыру. Содан

кейін 6-қадамды орындау керек.

4-қадам. рекурренттік қатынасын орындау және K параметрін бір санға көтеру: K=K+1.

5-қадам. j = j+1 деп аламыз.

6-қадам. j >N шартын тексеру, мұндағы N -модельденетін тізбектің берілген ұзындығы. Бұл шарт орындалған жағдайда 2-қадамға көшеміз.

7-қадам. Модельдеу нәтижесін шығару.

Д.И.Голенко өзінің ұсынған қалыптан ауытқу әдісі, кездейсоқ сандар тізбегінің ұзындығын есе ұзартатынын көрсетті.

Осы тарауғақатысты бақылау сұрақтары

1. өрнегі бойынша алынған кездейсоқ сандар тізбегінің периоды Р=m болу үшін қандай шарттар орындалуы тиіс?

2. өрнегінің параметрлерін таңдау қандай шартпен анықталады?

3. Д.И. Голенконың "ауытқу" әдісі қандай заңдылықты модельдеу үшін қолданылады?

4. формуласы қандай аралықтағы сандарды модельдеуге қолданылады?

5. формуласы қандай әдіске жатады?