Методология Бокса—Дженкинса

Экономические временные ряды за редким исключением нестационарны. Нестационарность чаще всего проявляется в наличии зависящей от времени неслучайной составляющей f(t). Если случайный остаток, полученный вычитанием из исходного ряда его неслучайной составляющей f(t), представляет собой стационарный временной ряд, то исходный ряд называется нестационарным однородным.

Для описания таких рядов используется модель авторегрессии — проинтегрированного скользящего среднего АРПСС(р, d, q) или в англоязычном варианте AutoregRessive Integrated Moving Average mode, (ARIMA-model). В специальной литературе она также известна как модель Бокса—Дженкинса, по имени авторов, разработавших этот подход и методологию моделирования.

Модель ARIMA используется для описания временных рядов, обладающих следующими свойствами:

1) ряд включает (аддитивно) составляющую f(t), имеющую вид алгебраического полинома;

2) ряд, получившийся после применения к нему d разпроцедуры последовательных разностей, может быть описан моделью ARMA(p, q).

В эконометрических исследованиях наиболее распространены модели ARIMA(p, d, q), значения параметров которой не превышают числа 2. При этом параметры р и q определяют порядок авторегрессионной составляющей и порядок скользящего среднего (аналогично модели ARMA(р, q)) соответственно, а параметр d — порядок разности (дискретной производной).

 

Рис.1.Схема подбора модели ARIMA

 

Временной ряд после взятия последовательных разностей (дискретного дифференцирования k-го порядка) может оказаться стационарным, удовлетворяющим модели ARMA(p, q):

D^kу_t = a₁ y_t-1 + a₂ y_t-2 + _… + a_p y_{t-p +} e_p - q₁ e_t-1 -

- q₂ e_t-2 - … - q_qe_t-q , (3.33)

где D^kу_t, - k-я последовательная разность уровней ряда y_t.

Очевидно, что из модели для D^kу_t легко получить модель для исходного ряда. Например, для модели Dу_t это можно сделать с помощью выражения

у_t = у_t + Dу_t .

Поясним содержание некоторых блоков, показанных на рис. 1. Сначала (в блоке 1, 2) необходимо получить стационарный ряд. При тестировании исходных данных на стационарность прежде всего используется визуальный анализ графика. Например, уже на этом этапе можно обнаружить ярко выраженную трендовую или сезонную составляющую.

Также в методике Бокса-Дженкинса рекомендуется проводить анализ АКФ (или ЧАКФ). Быстрое убывание значений выборочной АКФ — простой критерий стационарности (аналогичное поведение должна демонстрировать и ЧАКФ).

Для перехода к стационарному ряду традиционно применяют оператор взятия последовательных разностей (процедуру дискретного дифференцирования). Для определения значения параметра d (порядка разности) может быть использован эвристический критерий S²(k). Для вычисления его по формуле

S²(k) =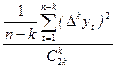

необходимо вычислить последовательные разности k = 1, 2, …, n для исходного ряда y₁, y₂, …, y_n как

D^kу_t = D^k-1у_t - D^k-1у_t-1 .

Начиная с некоторого значения k = k₀ ,величина S²(k) начинает стабилизироваться, оставаясь примерно на одном уровне при дальнейшем увеличении k. Тогда оценка порядка дискретной производной нестационарного временного ряда при построении ARIMA-модели d = k₀ – 1.

Также о том, что необходимая для стационарности ряда степень разности достигнута, будет свидетельствовать быстрое затухание АКФ. В практических исследованиях d, как правило, не превышает 2.

В блоке 3 после получения стационарного ряда исследуется характер поведения выборочных АКФ и ЧАКФ и выдвигаются гипотезы о значениях параметров р (порядок авторегрессии) и q (порядок скользящего среднего). При этом следует иметь в виду, что выборочные корреляционные функции могут не демонстрировать детального сходства с теоретическими значениями. Например, умеренно большие значения выборочной АКФ могут наблюдаться после затухания теоретической функции, а также могут наблюдаться всплески, не имеющиеся в теоретической функции. Поэтому для идентификации модели нужно использовать только главные черты АКФ, не обращая внимания на более тонкие детали. На выходе блока 3 может формироваться базовый набор, включающий 1,2 или даже большее число моделей.

В блоке 4 после осуществления идентификации моделей необходимо оценить их параметры. В современных эконометрических ППП используются разные подходы (МНК, нелинейный МНК, метод максимального правдоподобия (ММП)). Все эти оценки при больших объемах выборок асимптотически эквивалентны.

В блоке 5 для проверки каждой пробной модели на адекватность анализируется ее ряд остатков. У адекватной модели остатки должны быть похожими на белый шум, т.е. их выборочные автокорреляции не должны существенно отличаться от нуля.

При проверке значимости коэффициентов АКФ используются два подхода:

• проверка значимости каждого коэффициента автокорреляции отдельно;

• проверка значимости множества коэффициентов автокорреляции как группы.

Первый подход опирается на работу Бартлетта, показавшего, что если модель адекватна исходным данным и ошибки представляют собой белый шум, то распределение коэффициентов автокорреляции приближается к нормальному закону с нулевым математическим ожиданием и дисперсией 1/n, т.е. к N(0; 1/n). Поэтому если выборочный коэффициент автокорреляции r_k с вероятностью P = 1 - a выходит за границы доверительного интервала ± t_a/ , то нулевая гипотеза о равенстве нулю коэффициента r_k отвергается.

Второй подход опирается на Q-статистику Бокса—Пирса, позволяющую проверить равенство нулю сразу t первых значений АКФ остатков.

Q-статистика определяется как

. (3.34)

При нулевой гипотезе об отсутствии автокорреляции статистика Q имеет Хи-квадрат распределение c n = t - р - q степенями свободы, где р, q — параметры ARMA-модели.

Если Q > , то как группа первые t коэффициентов автокорреляции значимы (т.е. не все r₁, r₂, ..., r_t равны нулю). В некоторых эконометрических пакетах включена модификация этого подхода — тест Бокса—Льюнга. Соответствующая статистика в этом случае определяется выражением:

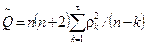. (3.35)

имеет такое же асимптотическое распределение, как и Q, однако ее распределение ближе к для конечных выборок. В практических руководствах рекомендуется рассматривать t = n/4 (но не более 50). Кроме того, при построении модели ARIMA необходимо проверить значимость коэффициентов (по t-критерию). При этом модель не должна содержать лишних параметров, т.е. уменьшение числа параметров будет способствовать появлению значимой автокорреляции остатков.

Если в результате проверки несколько моделей оказываются адекватны исходным данным, то при окончательном выборе сле­дует учесть два требования:

• повышение точности (качество подгонки модели);

• уменьшение числа параметров модели.

Для оценки качества модели эконометрических пакетах прикладных программ используются АКФ и ЧАКФ остаточного ряда, статистические характеристики оценок параметров модели, представительный набор статистических критериев.

Однако окончательный выбор модели все же должен оставаться за исследователем-экономистом, хорошо представляющим предметную область. Иногда можно построить две модели, которые одинаково хорошо соответствуют данным на ретроспективном участке (например, модель с порядком дифференцирования d=1 и AR-членами и модель с большим порядком дифференцирования и МА-членами). Однако предлагаемые прогнозы у этих моделей могут существенно различаться. Поэтому окончательный выбор между такими моделями должен опираться на представления исследователя о виде нестационарности исходного ряда, о характере его трендовой составляющей.

Успех применения мощного, гибкого, но в то же время сложного аппарата модели ARIMA во многом зависит от опыта и квалификации исследователя, а компьютерные программы автоматического выбора вида модели способны только снизить трудоемкость сложных вычислений.

4 Основные проблемы эконометрического
моделирования

Характерные особенности методологии эконометрического моделирования, с которыми приходится сталкиваться экономисту при работе с эконометрическими методами, сформулированы одним из ведущих современных исследователей - эконометриков Дэвидом Хендри. следующим образом:

“Проблемы в эконометрии многочисленны и разнообразны. Экономика — это сложный, динамический, многомерный и эволюционирующий объект, поэтому изучать ее трудно. Как общество, так и общественная система изменяются со временем, законы меняются, происходят технологические инновации, поэтому найти в этой системе инварианты непросто. Временные ряды коротки, сильно агрегированы, разнородны, нестационарны, зависят от времени и друг от друга, поэтому мы имеем мало эмпирической информации для изучения. Экономические величины измеряются неточно, подвержены значительным позднейшим исправлениям, а важные переменные часто не измеряются или вообще не могут быть измерены. Поэтому все наши выводы неточны и ненадежны. Экономические теории со временем меняются, соперничающие объяснения сосуществуют друг с другом, и поэтому надежная теоретическая основа для моделей отсутствует. И среди самих эконометристов, по-видимому, нет согласия по поводу того, как следует заниматься их предметом”.

При использовании эконометрических методов исследователь сталкивается с огромным количеством сложных проблем, что делает полученные им результаты недостаточно надежными и спорными. Поэтому должны быть веские причины, побуждающие использовать эти методы. Отметим некоторые из них.

Во-первых, не существует альтернативы статистическим методам в поиске общих закономерностей, связывающих наблюдаемые эмпирические факты. Поскольку любое измерение связано со случайными ошибками, то применение статистики неизбежно, кроме тех случаев, когда ошибки пренебрежимо малы. Результаты экономических измерений нельзя отнести к разряду точных чисел. Кроме того, многие экономические факторы являются ненаблюдаемыми и неизмеряемыми, либо данные о них отсутствуют, и эти ненаблюдаемые величины приходится считать случайными. Таким образом, хочет этого исследователь или нет, он всегда получает оценки, имеющие некоторое случайное распределение. Если не использовать статистические методы, то вероятностные свойства получаемых оценок остаются неизвестными.

Предположим, что исследователь получил оценку определенной величины, которая оказалась положительным числом. Может ли он быть уверенным, что полученный результат значим, а не является случайным совпадением? Эконометрические методы позволяют формально проверить гипотезу о знаке полученной оценки.

Не будет преувеличением утверждать, что любой вывод о наличие наблюдаемой закономерности делается, осознано или неосознанно, исходя из того, насколько вероятно было бы такое сочетание данных при отсутствии связи. Если такое случайное совпадение представляется маловероятным, тогда с уверенностью делается вывод о наличии связи. Но описанная процедура есть ни что иное, как неформальное описание проверки статистической гипотезы определенного вида. И, по-видимому, предпочтительнее применять менее субъективные формальные процедуры, что переводит получаемые результаты на универсальный язык статистики и стандартизирует их.

Чрезвычайную важность применения унифицированных процедур демонстрирует нам история физики. В экспериментальной физике этот процесс выразился в использовании стандартизированного лабораторного оборудования, в использовании стандартных методов проведения экспериментов и измерений. По сути дела речь шла о возникновении широко принятой культуры проведения экспериментов и измерений. Экономика точно также нуждается в унификации процедур, применяемых при обработке данных и моделировании.

Во-вторых, применение эконометрии не исключает применения других прикладных методов. Эконометрические методы следует рассматривать скорее как своеобразный инструмент, чем как самостоятельное прикладное моделирование.

Эконометрические методы позволяют не только получить оценки, но и проверить гипотезы, лежащие в основе используемой модели экономического явления, выявить, какие гипотезы нарушаются, и указать, в каком направлении следует модифицировать модель. Большинство серьезных проблем, с которыми приходится сталкиваться при эконометрическом моделировании, на самом деле носят общий характер для экономической науки, поскольку они связаны с характером самого предмета исследований — экономических процессов.

Невозможность использования эконометрических методов и применение вследствие этого каких-то других методов является с этой точки зрения проблемой, а не достоинством.

Другой вопрос заключается в том, следует ли вообще моделировать экономические процессы. Можно предложить следующий аргумент: люди всегда, рассуждая об экономике, держат в голове некоторую неформализованную “модель” или “теорию”. Отличие ученого-экономиста заключается в том, что он в явном виде выписывает ту модель, с которой работает. Поэтому может выявить, на каких именно предположениях он основывается, может увидеть слабые места своей концепции.