Основные характеристики временных рядов

Анализируемый временной ряд может рассматриваться как одна частная реализация стохастического процесса. Специальный случай стохастических процессов представляют стационарные процессы, когда отдельная реализация служит «полномочным представителем» всей совокупности возможных реализаций случайного процесса. Рассмотрим формальное определение стационарности.

Ряд называется строго стационарным (strictly stationary) или стационарным в узком смысле, если совместное распределение n наблюдений y_tl, y_t2, , y_tn такое же, как и для n наблюдений, смещенных на промежуток времени t. Таким образом, свойства строго стационарного временного ряда не зависят от начала отсчета времени.

Исследователя обычно интересует не все распределение; а средние значения и ковариации. Поэтому на практике чаще пользуется понятие слабой стационарности (weak stationary) или стационарности в широком смысле.

В этом случае стационарность временного ряда связывается с требованиями того, чтобы он имел среднее, дисперсию и ковариацию, не зависящие от момента времени t:

M(y_t) = M(y_{t + t}.) = m;

D(y_t) = M[y_t - M(y_t)] ² = M[y_{t + t} - M(y_{t + t})]² = g(0);

Cov(y_t, y_t+t) = M[(y_t - m )(y_{t + t} -m )] = g(t);

При дальнейшем изложении под термином «стационарность» будет рассматриваться слабая стационарность. Это означает, что автоковариация будет зависеть только с сдвига по времени t и не будет зависеть от t.

Здесь ковариация Cov(y_t, y_t+t) называется автоковариацией (и обозначаетсяg(t) ), так как характеризует статистическую связь между уровнями одного и того временного ряда, отстоящими на t временных тактов. При анализе изменения g(t) в зависимости от временного сдвига t принято говорить об автоковариационной функции (autocovariation function). Очевидно, что при t = 0 автоковариационная функция g(0) равна дисперсии временного ряда Cov(y_t, y_t) = D(y_t).

С понятием автоковариационной функции тесно связана автокорреляционная функция, АКФ (autocorrelation function, ACF):

r(t) = Cov(y_t, y_t+t)/ D(y_t) = g(t)/ g (0).

Значения АКФ также характеризуют тесноту (степень) статистической связи между уровнями временного ряда, разделенными t временными тактами. Однако в отличие от значений автоковариационной функции они безразмерны, не зависят от масштаба измерения уровней исследуемого временного ряда и подчиняются ограничению

| r(t) | £ 1 (очевидно, что r(0) = 1).

Из условия стационарности следует, что r(t) = r(-t), поэтому при рассмотрении поведения АКФ ограничиваются лишь областью положительных значений t.

На практике значения АКФ статистически оцениваются по имеющимся уровням временного ряда. Выборочная оценка коэффициента автокорреляции r(t) может быть определена следующим образом:

r(t) =

где n — длина временного ряда y_l, y₂, ..., у_n; t — временной сдвиг (т = 1, 2, ..., n — 1); — оценка среднего значения, найденная по формуле:

.

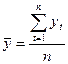Отметим, что числитель выражения r(t) представляет выборочную оценку коэффициента автоковариации. Иногда график АКФ, отражающий изменение r(t) в зависимости от сдвига t называют коррелограммой (correlogram).

Очевидно, что с увеличением значения лага t число пар наблюдений (n - t), используемых для расчета, уменьшается. Поэтому в практических руководствах рекомендуется поддерживать соотношение t £ n/4.

Для стационарного временного ряда с увеличением t автокорреляционная функция должна демонстрировать свойство монотонного убывания по абсолютной величине, так как взаимосвязь между уровнями ряда с ростом t ослабевает. Однако это условие может нарушаться для выборочных значений АКФ.

Идея перенесения частной корреляции, «очищенной» взаимосвязи, на временные ряды находит свое выражение в частной автокорреляционной функции, ЧАКФ (partial autocorrelation function, РАСЕ). С помощью ЧАКФ измеряется корреляция между уровнями ряда y_t, и y_t+t , разделенными t временными тактами, при исключении влияния на эту взаимосвязь всех промежуточных уровней ряда y_t+1, y_t+2, , y_t+t-1.

return false">ссылка скрыта

Например, коэффициент частной автокорреляции r_ч(t) при t = 2 будет определять корреляцию между уровнями временного ряда, разделенными двумя тактами времени, при условии, что значения промежуточных уровней зафиксированы на среднем уровне:

r_ч(2) = r( y_t , y_t+2 | y_t+1 = m).

В эконометрических пакетах присутствует возможность по строения графика ЧАКФ, на котором показаны выборочные оценки коэффициентов частной автокорреляции в зависимости от лагов t.

Очевидно, что коэффициент частной автокорреляции r_ч(1) для лага t = 1 будет равен коэффициенту автокорреляции r (1), так как при этом значении t нет промежуточных лагов. Но при t > 1 уже появятся отличия в значениях этих коэффициентов.

Примером стационарности служит “белый шум” (white noise). Процессом белого шума (“белым шумом”,“чисто случайным временным рядом”) называют стационарный временной ряд, в данном случае случайная величина e_t, которая удовлетворяет следующим условиям:

M(e_t) = 0;

M(e_t e_t) = D(e_t) = g(0)= > 0;

М(e_t, e_t±t) = Cov(e_t, e_t±t) =g(t) = 0 при t ¹ 0.

(причем постоянная дисперсия не зависит от t).

В качестве примера “белого шума” можно привести остатки, рассматриваемые в классической линейной регрессионной модели. В случае нормального распределения остатков они образуют гауссовский “белый шум”. Следует подчеркнуть, что “белый шум” не обязательно должен подчиняться нормальному распределению, в то же время нормальный (гауссовский) “белый шум” удовлетворяет всем этим условиям.

В заключение отметим, что вид АКФ и ЧАКФ оказывает существенную помощь в выборе моделей, описывающих поведение анализируемых временных рядов.