Методичні рекомендації до розрахунку зубчастої циліндричної передачі зовнішнього зачеплення

 

4.1. Вибрати із таблиці 3.12 [3, с. 65] чи з інших джерел механічні характеристики вказаних у завданні матеріалів зубчастих коліс після термообробки, враховуючи при цьому рекомендації щодо співвідношення твердостей шестірні і колеса (див. п. 3).

4.2. Визначити за формулами (3.51) і (3.52) [3, с. 77, 117] допустимі напруження згину для шестірні і колеса:

.

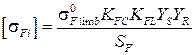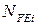Прийняти при цьому: базове число зміни циклів напружень ; сумарні числа циклів зміни напружень для шестірні і колеса вирахувати за формулами (3.54) [3, с. 70, 77] і (3.37') [3, с. 75, 117]. Інші параметри і коефіцієнти, які входять у формули (3.51) і (3.52), прийняти згідно з рекомендаціями [3, с. 77–79; 117–118].

4.3. Визначити за формулами (3.33) і (3.34) [3, с. 74, 118] допустимі напруження на контактну витривалість окремо для шестірні і колеса:

,

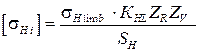де — коефіцієнти довговічності зубчастих коліс, які враховують проектний термін роботи передачі та режим її навантаження і залежать від співвідношення базових чисел циклів зміни напружень і сумарних чисел циклів зміни напружень для шестірні і колеса .

Сумарні числа циклів зміни напружень при розрахунках передачі на контактну витривалість прийняти = 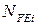(див. п. 4.2), а базові числа зміни напружень визначаються, залежно від твердості робочих поверхонь зубів, за допомогою графіка = ( ) [3, рис. 3.16, с. 74]. Наприклад, при твердості активних поверхонь зубів НВ = 300 базове число циклів = 25·10⁶.

Таким чином, якщо > , то для зубчастих коліс передач зі змінним навантаженням = 1, а для коліс передач з постійним навантаженням [3, с. 75, 118]:

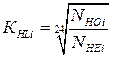≥ 0,9.

У цьому випадку для знаходження коефіцієнта потрібно прологарифмувати дане рівняння, або скористатись графіком залежності = 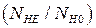(рис. 4.1), [11, с. 184].

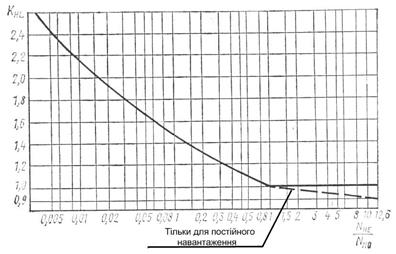
Рис. 4.1 — Залежність коефіцієнта від співвідношення чисел циклів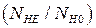

У випадку < , розрахункові значення обмежують. Для коліс з об’ємним зміцненням зубів (після нормалізації, поліпшення) приймають ≤ 2,6, а для коліс із поверхневим зміцненням (СВЧ, цементація, азотування) приймають = 1,8 [3, с. 75].

Інші параметри і коефіцієнти, які входять у формули (3.33) і (3.34), прийняти згідно з рекомендаціями [3, с. 74–76, 118].

4.4. Визначити допустиме контактне напруження передачі. Для прямозубих передач в якості допустимого напруження 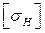приймають допустиме контактне напруження того зубчастого колеса, для якого воно менше:

Для косозубих і шевронних зачеплень допустиме контактне напруження передачі визначають за середнім напруженням:

При цьому повинна виконуватись умова [3, с. 76, 119]:

,

де 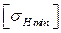менше з двох значень і .

Якщо вказана умова не виконується, приймають [3, с. 76]: .

4.5. Розрахувати основні параметри передачі із умови її контактної витривалості. Початковий діаметр шестірні 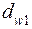обчислити за формулою (3.16) [3, с. 69, 119]. Слід зауважити, що використання формули (3.16') [3, с. 69], або формул для визначення міжосьової відстані , наведених у ряді навчальних посібників: [1, с. 56, 62]; [5, с. 309]; [7, с. 309], [11, с. 213]; [15, с. 13], згідно з ГОСТ 21354-87 вимагає виконання повного перевірного розрахунку передачі, який включає обчислювальних операцій вдвічі більше, ніж проектувальний розрахунок [21; 3, с. 76].

Для визначення ряду параметрів, які входять до формули (3.16), необхідно попередньо вирахувати орієнтовну колову швидкість υ коліс на початковому діаметрі за формулою (3.27) [3, с. 72; 119] і визначити за таблицями 3.32 та 3.33 [3, с. 90] потрібний ступінь точності зубчастих коліс і передачі.

Коефіцієнт , який враховує розподілення навантаження між зубами у нормальній площині, де вимірюється кут зачеплення , визначається за рекомендаціями [3, с. 72].

Коефіцієнт ширини зубчастого вінця, який суттєво впливає на габарити і масу передачі слід визначити за рядом показників [3, с. 71–72; 119; 58–60; табл. 3.3 і 3.7]. При цьому варто скористатися такими рекомендаціями: коефіцієнт торцевого перекриття прийняти для прямозубих передач ≥ 1,2, для косозубих і шевронних передач ≥ 1,0; мінімальна кількість зубів шестірні для прямозубих передач z_1min = 17, а для косозубих можна скористатись таблицею 3.3 [3, с. 58], — при цьому також врахувати, що для коліс із твердістю зубів Н₀₁ ≤ 350 НВ раціонально попередньо приймати z₁ = 18…35, а для коліс із твердістю зубів Н₀₁ > 350 НВ — z₁ = 15…32; кут нахилу зубів для косозубих коліс приймають (рідко до 25°); для роздвоєних ступенів редукторів , а для шевронних коліс , причому, для шестірні рекомендують приймати ліве направлення зубів, а для коліс — праве. Після уточнення параметрів z₁, z₂, β остаточно визначають коефіцієнт за формулою (3.3) [3, с. 60] і коефіцієнт за формулою (3.26) [3, с. 71; 119].

Коефіцієнт , який враховує нерівномірність розподілу навантаження по ширині вінця, визначається за допомогою графіків [3, с. 73; рис. 3.14]. Наприклад, для одноступінчастого циліндричного редуктора (схема № 6 на рис. 3.14, а) при твердості зубів хоча б одного з коліс менше 350 НВ і коефіцієнті = 1,8 коефіцієнт = 1,15 [3, с. 73, рис 3.14, б].

Коефіцієнт , який враховує динамічне навантаження в зачепленні залежно від колової швидкості v, ступеня точності і твердості зубів колеса знаходиться інтерполюванням значень за таблицею 3.16 [3, с. 72], причому в чисельниках наведені значення для прямозубих передач, а в знаменниках — для косозубих.

Наприклад, для конкретного випадку розрахунку косозубої циліндричної передачі [3, с. 119] з параметрами: ν = 2,75 м/с; 9-а ступінь точності і твердість зубів колеса менше 350 НВ, коефіцієнт визначається інтерполюванням його значень в інтервалі між ν = 2 м/с (1,03) і ν = 4 м/с (1,05) в такому порядку [3, с. 72]:

1) 1,05 – 1,03 = 0,02;

2) ;

3) 1,03 + 0,0075 = 1, 0375 ≈ 1,038.

Інші параметри і коефіцієнти, які входять у формулу (3.16), прийняти згідно з рекомендаціями [3, с. 71–76; 119–120].

4.6. Враховуючи що проектована передача некоригована, прийняти = 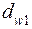і визначити розрахунковий модуль зачеплення за формулами (3.45) або (3.46) [3, с. 76, 120] відповідно для прямозубих або для косозубих (шевронних) передач. Округлити розрахунковий модуль до найближчого більшого стандартного значення за ГОСТ 9563-80, але не менше 1,5 мм [3, с. 254, табл. 9]:

1-й ряд (переважного застосування): 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20;

2-й ряд: 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18.

По стандартному модулю m за вищевказаними формулами уточнити значення ділильного і початкового 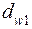діаметрів шестірні.

4.7. Виконати перевірний розрахунок передачі на контактну витривалість. Для цього по уточненому у п. 4.6 діаметру 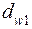шестірні обчислити за формулою (3.47) [3, с. 76, 120] дійсну колову швидкість v коліс і визначити по ній за таблицею 3.33 [3, с. 90] потрібну ступінь точності передачі, яка може і не відрізнятись від знайденої попередньо у п. 4.5. По дійсним швидкості і ступеню точності уточнити коефіцієнти: [3, с. 72, рис. 3.13] (для косозубих і шевронних коліс); [3, с. 72, табл. 3.16] і Z'v [3, с. 76, рис. 3.17], які, на відміну від знайдених попередньо у п. 4.5, позначаються штрихом.

return false">ссылка скрыта

Уточнити початковий діаметр шестірні за формулою (3.48) [3, с. 76, 120] і по ньому, за формулами (3.45) для прямозубих або (3.46) для косозубих (шевронних) передач, перерахувати модуль зачеплення m .

Якщо модуль m ≤ m, або несуттєво (в межах 10%) перевищує m, то залишити параметри m, і 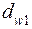, визначені у п. 4.6, без змін. Якщо ж модуль m суттєво перевищує значення m, то його слід знову округлити до найближчого більшого стандартного значення, вирахувати нові значення і 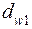і повторити перевірний розрахунок на контактну витривалість за п. 4.7.

4.8. За допомогою визначеного у п. 4.5 коефіцієнта вирахувати ширину зубчастого вінця за формулою [3, с. 55, 120] і прийняти його значення зі стандартного ряду лінійних розмірів за ГОСТ 6636-69 [3, с. 249, табл. 1].

4.9. Виконати перевірний розрахунок зубів на витривалість по напруженням згину. Розрахункове напруження згину для зубів шестірні та умова їхньої згинальної витривалості визначається за формулою (3.17) [3, с. 69, 120]:

,

а для зубів колеса за формулою (3.17') [3, с. 69, 121]:

В свою чергу, розрахункове питоме колове навантаження обчислюється за формулою (3.25') [3, с. 71, 121]:

Значення коефіцієнтів форми зуба для циліндричних коліс приймають за графіком [3, с. 77, рис. 3.18] залежно від коефіцієнтів зміщення х і кількості зубів z прямозубого колеса, або від кількості зубів z_v уявного, так званого еквівалентного прямозубого колеса, зорієнтованого по відношенню до проектованого косозубого колеса під кутом β таким чином, щоб профілі його зубів проектувались на площину, нормальну до напряму руху різального інструмента і визначали дійсні форму і розміри зубів косозубого колеса в нормальному перерізі. Еквівалентна кількість зубів окремо для шестірні і колеса вираховується за формулами [3, с. 76, 120]:

; .

Коефіцієнт , який враховує нерівномірність розподілу навантаження по ширині вінця, як і подібний коефіцієнт визначається за допомогою графіків [3, с. 73, рис. 3.14, г, д] залежно від номера схеми редуктора, твердості поверхонь зубів і коефіцієнта ширини зубчастого вінця (див. п. 4.5).

Коефіцієнт , який враховує динамічне навантаження передачі, як і подібний коефіцієнт знаходиться інтерполюванням за табл. 3.16 [3, с. 72] (див. п. 4.5).

Інші параметри і коефіцієнти, які входять у формули (3.17) і (3.25'), прийняти згідно з рекомендаціями [3, с. 76–79, 120–121].

Перевірити умову згинальної витривалості зубів шестірні і колеса за формулами (3.17) і (3.17'). У випадку недотримання вказаної умови, міцність зубів на згин для передачі з відомими геометричними параметрами зубчастих коліс можна підвищити, збільшуючи модуль за стандартним рядом (див. п. 4.6) та зменшуючи відповідно кількості зубів шестірні і колеса за формулами (3.45) або (3.46) [3, с. 76]:

або .

У разі такого коректування параметрів передачі m, z₁ і z₂, перевірний розрахунок зубів на витривалість по напруженням згину потрібно повторити за п. 4.9.

4.10. Прийняти остаточно основні параметри передачі [3, с. 55, 57–59, 121].

В результаті проектувальних і перевірних розрахунків у пп. 4.1–4.9 були визначені і уточнені нижчевказані параметри: u, m, z₁, z₂, β, b_w, = .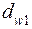

З метою подальшого проектування редуктора та його деталей необхідно також визначити наступні параметри [3, с. 121].

Початковий і ділильний діаметри зубчастого колеса

Міжосьову відстань (проектувальний і перевірний розрахунок):

При необхідності округлення міжосьової відстані до цілого числа, наприклад, згідно з параметричним рядом [3, с. 249, табл. 1] чи з метою вписування передачі у задану міжосьову відстань слід перерахувати кут нахилу зубів за формулою (3.2') [3, с. 58]:

з наступним перерахунком початкових діаметрів і і перевіркою міжосьової відстані [3, с. 121].

4.11. Визначити ряд параметрів зачеплення, які наносять на робочих кресленнях зубчастих коліс та вказують у стандартних таблицях на робочих кресленнях шестерень, зубчастих коліс, вал-шестерень [3, с. 111]:

– , — діаметри вершин зубів та впадин зубчастих коліс [3, с. 59];

– , — довжина постійних хорд зубів шестірні і колеса та висота головок зубів до постійних хорд [3, с. 96];

– — основний діаметр зубчастого колеса;

– — крок зачеплення;

– — осьовий крок зубчастого вінця.

4.12. Приклади проектувальних розрахунків ряду механічних передач наведені також в нижчевказаних джерелах:

– зубчастих циліндричних [1, 2, 5, 7, 8, 10, 11];

– зубчастих конічних [1, 2, 5, 7, 8, 10, 11];

– черв’ячних [1, 2, 5, 7, 8, 10, 11];

– плоскопасових [1, 2, 5, 7, 8, 11];

– клинопасових [1, 2, 5, 8, 10, 11];

– ланцюгових [1, 2, 5, 10, 11].

 

5. Методичні рекомендації до розрахунку
зубчастих конічних прямозубих передач

 

5.1. Конічні передачі розраховуються на міцність за методикою, аналогічною методиці розрахунку циліндричних передач, але при цьому конічні зубчасті колеса замінюються так званими еквівалентними циліндричними колесами, форма зубів у яких така ж, як у нормальних перерізах зубчастих вінців конічних коліс. Формули для розрахунку на міцність конічних зубчастих коліс аналогічні формулам для розрахунку циліндричних коліс, але в них вводять коефіцієнт, який враховує пониження навантажувальної здатності зубів конічної передачі на 15%.

Розрахунок геометричних параметрів зубчастої конічної передачі здійснюють за ГОСТ 19624-74. Чинний стандарт поширюється на зубчасті конічні передачі з прямими пропорційно понижуваними зубами зовнішнього зачеплення, виконаними за осьовою формою I [3, с. 61]. Ця форма є основною для прямозубих і косозубих конічних передач і пропонується як вихідна у завданнях на курсовий проект. Форми II і III застосовуються для конічних коліс з круговими зубами [3, с. 61].

Для конічних некоригованих прямозубих передач форми I за стандартний приймається зовнішній коловий модуль [3, с. 62, 254, табл. 9]:

чисельно рівний стандартизованому нормальному модулю m циліндричних передач (див. п. 4.6).

5.2. Враховуючи вищесказане, методика вибору механічних характеристик матеріалів конічних зубчастих коліс та розрахунку допустимих напружень на згинальну і контактну витривалість зубів шестірні і колеса залишається такою ж, як і для циліндричних зубчастих коліс (див. п. 4.1–4.4), зокрема, в якості допустимого контактного напруження для розрахунку прямозубої конічної передачі приймається допустиме напруження того зубчастого колеса, для якого воно менше:

5.3. Розрахунок зубчастої конічної передачі починають з обчислення початкового діаметра шестірні по її зовнішньому (більшому) торцю за формулою (3.20) [3, с. 70]:

Аналогічно з розрахунком на контактну витривалість зубчастої циліндричної передачі (п. 4.5) для визначення ряду параметрів, які входять до формули (3.20), спочатку вираховують орієнтовну колову швидкість υ коліс на початкових діаметрах d_wi за формулою (3.27) [3, с. 72, 122] і визначають за таблицями 3.32 та 3.33 [3, с. 90] потрібний ступінь точності передачі.

5.4. Коефіцієнт , який враховує розподілення навантаження між зубами у нормальній площині, де вимірюється кут зачеплення α, прийняти згідно з рекомендаціями [3, с. 82]

5.5. Коефіцієнт ширини вінця прийняти за формулою (3.63) та рекомендацією (3.65) [3, с. 80]: = 0,25.

5.6. Коефіцієнт , який враховує нерівномірність розподілу навантаження по ширині вінця, визначається за допомогою графіків [3, с. 81, рис. 3.20, а]. Наприклад, для конкретного випадку розрахунку одноступінчастого конічного прямозубого редуктора з роликовими підшипниками в опорах валів [3, с. 122, 156] і параметрами передачі: схема виконання — I; НВ_1,2 ≤ 350; = 0,25; u = 5 та при відношенні , коефіцієнт = 1,15 [3, с. 81, рис. 3.20, а].

5.7. Коефіцієнт динамічного навантаження , як і подібний коефіцієнт при розрахунку циліндричної передачі, визначається методом інтерполювання за табл. 3.16 [3, с. 72], (див. п. 4.5), але за ступенем точності на одиницю грубішим за визначений у п. 5.3. Наприклад, для випадку розрахунку конічної прямозубої передачі 8-го ступеня точності [3, с. 122], коефіцієнт , при коловій швидкості υ = = 4,23 м/с, знаходять інтерполюванням його значень у чисельниках рядка для циліндричних прямозубих коліс 9-го ступеня точності [3, с. 72].

5.8. Значення коефіцієнта Z_H, який враховує форму спряжених поверхонь зубів, і коефіцієнта Z_M, який враховує механічні властивості матеріалів спряжених зубчастих коліс, визначити згідно з рекомендаціями [3, с. 73, 122].

5.9. Для знаходження коефіцієнта Z_ε, який враховує сумарну довжину контактних ліній, потрібно спочатку визначити кількість зубів z₁ шестірні і коефіцієнт торцевого перекриття ε_α. Згідно з рекомендаціями (див п. 4.5) для прямозубих передач з твердістю зубів Н₀₁ ≤ 350 НВ слід попередньо приймати ε_α ≥ 1,2 і z₁=18…35. Враховуючи вказані рекомендації, а також з метою мінімізації габаритів проектованої передачі, по табл. 3.11 [3, с. 63] доцільно прийняти z₁=18 і ε_α = =1,58.

В результаті, за формулою (3.30) [3, с. 74, 122] вираховують коефіцієнт Z_ε, а за формулою (3.20) [3, с. 122] вираховують початковий діаметр шестірні d_w1 (див. п. 5.3). При цьому слід врахувати, що у формулі (3.20) крутний момент Т₁ на валу шестірні має розмірність у ньютон-міліметрах, а у курсових проектах крутний момент на валу шестірні позначений символами Т₂ або Т₃ (в залежності від схеми привода) і вирахуваний у ньютон-метрах (див. табл. 2.4).

5.10. Обчислити зовнішній коловий модуль за формулою [3, с. 62, 122]:

мм.

Отриманий модуль округлити до найближчого більшого стандартного значення (див. п. 4.6), але не менше 1,25 мм.

Уточнити початковий діаметр шестірні d_w1 по стандартному модулю за вищенаведеною формулою.

5.11. Обчислити кількість зубів спряженого зубчастого колеса (z₂ = z₁·u), округлити z₂ до найближчого цілого числа і уточнити фактичне передаточне число зубчастої передачі (u = z₂ / z₁), яке може дещо відрізнятись від стандартного передаточного числа, прийнятого у розділі 2.2 (див. табл. 2.2).

5.12. Вирахувати кількість зубів уявного, так званого плоского колеса, побудованого на твірних зубчастих вінців спряжених конічних коліс за формулою [3, с. 62, 122]: .

5.13. Вирахувати зовнішню конусну відстань за формулою [3, с. 62, 122]:

.

5.14. Вирахувати робочу ширину зубчастого вінця, скориставшись вищеприйнятим коефіцієнтом = 0,25 (див. п. 5.5), за формулою (3.63) [3, с. 80, 122]:

.

5.15. Перевірити за формулою (3.64) [3, с. 80, 122] умову .

У випадку, якщо ця умова не дотримується, потрібно зменшити коефіцієнт ширини вінця до значення = 0,2, уточнити коефіцієнт (див. п. 5.7), перерахувати початковий діаметр шестірні d_w1 (див. п. 5.3) та виконати дії за пп. 5.10…5.15 [3, с. 122] з кінцевою метою дотримання умови за формулою (3.64).

5.16. Виконати перевірний розрахунок зубів на контактну витривалість. Для цього потрібно виконати такі операції.

Обчислити середній нормальний модуль зачеплення за формулою (3.4) [3, с. 61, 122]:

де = 1, оскільки середній кут нахилу зубів у прямозубих конічних передачах = 0.

Вирахувати середній початковий діаметр шестірні за формулою [3, с. 80, 122]:

Обчислити розрахункову колову швидкість на середньому початковому діаметрі шестірні за формулою (3.47) [3, с. 76, 122]:

.

Скоригувати по розрахунковій швидкості потрібний ступінь точності передачі за таблицею 3.33 [3, с. 90], який може і не відрізнятись від знайденого орієнтовного значення у п. 5.3.

Уточнити за графіком [3, с. 76, рис. 3.17] коефіцієнт Z'_v, який враховує вплив дійсної колової швидкості на діаметр шестірні, оскільки в попередніх розрахунках приймають Z_v = 1 [3, с. 75].

Уточнити по розрахунковій коловій швидкості коефіцієнт динамічного навантаження за табл. 3.16 [3, с. 72], але за ступенем точності на одиницю грубішим за скоригований (див. пп. 4.5 і 5.7).

Перерахувати за уточненими параметрами початковий діаметр шестірні d '_w1 по її більшому торцю за формулою (3.48) [3, с. 76, 123], визначити нове значення колового модуля за формулою і округлити його до найближчого стандартного значення (див. п. 4.6).

У випадку, якщо новий модуль збільшився у порівнянні із раніше визначеним стандартним модулем у п. 5.10, потрібно збільшити початковий діаметр шестірні за формулою та відповідно вирахувати нові значення конусної відстані R_e і робочої ширини зубчастого вінця b_w (див. пп. 5.13 і 5. 14).

5.17. Виконати перевірний розрахунок зубів на витривалість по напруженням згину.

Розрахункове напруження згину для зубів шестірні та умова їхньої згинальної витривалості визначається за формулою (3.22) [3, с. 70, 123]:

а для зубів колеса за формулою (3.22') [3, с. 70, 123]:

В свою чергу, розрахункове питоме колове навантаження обчислюється за формулою (3.25') [3, с. 71, 123]:

Числові значення ряду параметрів і коефіцієнтів, які входять до цих формул, та методика їхнього визначення наведені вище при розрахунках циліндричних і конічних передач, а саме: Т₁ (табл. 2.4); (п. 4.2); (п. 5.16); (п. 5.16); b_w (п. 5.14); = 1,0 [3, с. 77, 123]; = 1,0 [3, с. 82, 123].

Коефіцієнт подібно коефіцієнту визначається за допомогою графіків [3, с. 81, рис. 3.20, б] залежно від ряду параметрів (див. п. 5.6).

Коефіцієнт як і подібний коефіцієнт при розрахунку конічної передачі на контактну витривалість, визначається методом інтерполювання за табл. 3.16 [3, с. 72], але за розрахунковою швидкістю та ступенем точності передачі на одиницю грубішим за скоригований по даній швидкості (див. п. 5.16). Наприклад, для випадку розрахунку конічної прямозубої передачі 8-го ступеня точності [3, с. 123], коефіцієнт , при уточненій коловій швидкості = 4,23 м/с, знаходять інтерполюванням його значень у чисельниках рядка для циліндричних прямозубих коліс 9-го ступеня точності (див. пп. 4.5 і 5.7).

5.18. Для знаходження коефіцієнтів форми зубів , спряжених конічних коліс потрібно спочатку вирахувати еквівалентні кількості зубів для шестірні і колеса за формулою (3.7) [3, с. 62, 123]:

; ,

де = ar tg ; = Σ – — кути ділильних конусів відповідно шестірні і колеса; Σ = 90° — міжосьовий кут ортогональної конічної передачі [3, с. 62].

Тут принагідно відзначити, що уявні, так звані еквівалентні прямозубі конічні колеса, утворюються на розгортках бічних поверхонь зовнішніх ділильних додаткових конусів, на яких профілюються зуби проектованих конічних коліс.

Числові значення коефіцієнтів , приймають за графіком [3, с. 82, рис 3.21] залежно від коефіцієнта зміщення вихідного контуру х (для некоригованих передач х = 0) та еквівалентних кількостей зубів , [3, с. 82, 123].

5.19. Перевірити умову згинальної витривалості зубів шестірні і колеса за формулами (3.25'), (3.22) і (3.22') (див. п. 5.17), яка звичайно виконується [3, с. 123].

У випадку недотримання вказаної умови, потрібно збільшити зовнішній коловий модуль до найближчого більшого стандартного значення (див. п. 4.6), визначити нові значення параметрів , b_w, , за пп. 5.13–5.16 і повторно перевірити умову згинальної витривалості зубів шестірні і колеса за формулами (3.25'), (3.22) і (3.22') (див. п. 5.17).

5.20. Прийняти остаточно основні параметри конічної прямозубої передачі [3, с. 55; 57; 62; 124].

В результаті проектувальних і перевірних розрахунків у пп. 5.1–5.18 було визначено і уточнено ряд параметрів: u, m_te, z₁, z₂, z_c, ( 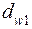), , b_w, , ( ), , , Σ, ступінь точності передачі.

З метою подальшого проектування редуктора і його деталей та визначення параметрів зачеплення, які наносять на робочих кресленнях зубчастих коліс та вказують у стандартних таблицях на робочих кресленнях, необхідно також обчислити такі параметри зубчастих вінців [3, с. 62; 99–101; 112]: ( ); ( ); ; h_e; h_aei; h_fei; d_aei; ; ; ; .

 

6. Методичні рекомендації до розрахунку черв’ячних передач
з циліндричними черв’яками

 

6.1. Черв’ячні передачі відносяться до зубчасто-гвинтових передач, а тому методика їхнього розрахунку дещо відрізняється від методики розрахунку зубчастих евольвентних циліндричних і конічних передач (див. п. 3).

У зв’язку з високими швидкостями ковзання і несприятливими умовами змащування у черв’ячному зачепленні матеріали черв’ячної пари повинні мати антифрикційні властивості, гарну припрацьовуваність, зносостійкість і підвищену теплопровідність. Для цього у черв’ячній парі сполучають різнорідні матеріали [1, 3, 5–8, 10, 11, 15].

Черв’яки виготовляють зі сталей 45, 20Х, 40Х, 40ХН, 30ХГН, 20ХГР, 20ХН3А, 30ХГС, 38ХГН, 35ХМА, 18ХГТ та ін. методом нарізання на токарному верстаті або дисковою фрезою на черв’ячно-фрезерному верстаті.

Найбільшу навантажувальну здатність мають черв’яки із цементованих сталей 20Х, 20ХГР, 20ХН3А, 18ХГТ з твердістю після гартування 56…63 HRC та шліфованими і полірованими поверхнями витків. Черв’яки зі сталей 40Х, 40ХН, 30ХГН, 38ХГН з твердістю після операцій поліпшення, нормалізації та гартування 45…55 НRС звичайно застосовують у тихохідних і малонавантажених передачах а також при відсутності обладнання для шліфування. При цьому допускається застосування черв’яків з твердістю НВ ≤ 350 нешліфованих.

Вибір матеріалу вінців черв’ячних коліс визначається швидкістю ковзання υ_к і довготривалістю роботи. Звичайно вінці черв’ячних коліс виготовляють із бронзи, латуні, сірого чавуну. Високі антифрикційні властивості мають олов’яні бронзи Бр010Ф1, Бр010Н1Ф1, Бр06Ц6С3, Бр05Ц5С5 тощо, які використовують при високих швидкостях ковзання υ_к = 12…35 м/с, але вони дорогі і дефіцитні. При середніх швидкостях ковзання υ_к = 3…10 м/с застосовують безолов’яні алюмінієві бронзи БрАЖ9-4, БрА9Ж3Л, БрА10Ж4Н4Л, латунь ЛЦ38Мц2С2 та інші.

При малих навантаженнях і швидкості ковзання υ_к ≤ 3 м/с черв’ячні колеса можна виготовляти із сірих чавунів СЧ15, СЧ18, СЧ20, СЧ25.

Колісні центри звичайно виготовляють із сталі 45Л з відливанням у піщані форми.

Таким чином, оскільки в черв’ячних передачах черв’як і колесо виготовляються із різнорідних матеріалів, які значно відрізняються механічними характеристиками, їхній розрахунок проводиться по менш міцному елементу — черв’яч-ному колесу. Окрім викришування робочих поверхонь зубів колеса у черв’ячній передачі також має місце їхнє заїдання і зношення, які залежать від діючих контактних напружень у зачепленні. А тому для закритих черв’ячних передач основним є розрахунок на контактну витривалість зубів, а перевірними і додатковими — розрахунки зубів на згинальну витривалість, контактну і згинальну міцність від максимального навантаження, відсутність заїдання та нагрівання редуктора.

Методику проектувального розрахунку черв’ячних передач на контактну витривалість та перевірних і додаткових розрахунків розроблено згідно з положеннями ДСТУ 2458-94, ГОСТ 21354-87 та ряду рекомендацій, які не суперечать стандартній методиці [1, 3, 5–8, 10–12, 15]. Методику розрахунку геометричних параметрів черв’ячних передач розроблено відповідно до ГОСТ 19650-74 та ГОСТ 19036-81, які поширюються на черв’ячні передачі з циліндричними архімедовим (ZA) і евольвентним (Z1) черв’яками [3, с. 83–85].

6.2. Проектувальний розрахунок черв’ячної передачі починають з вибору матеріалів черв’ячної пари (черв’яка і колеса) та визначення їхніх механічних характеристик [3, с. 87, 131, табл. 3.30].

6.3. Узгодити попередньо прийняте передаточне відношення проектованої передачі з номінальним передаточним числом u_n для черв’ячних передач за ДСТУ 2458-94:

1-й ряд: 8; 10; 12,5; 16; 20; 25; 31,5; 40; 50; 63; 80;

2-й ряд: 9; 11,2; 14; 18; 22,4; 28; 35,5; 45; 56; 71.

6.4. Призначити відповідно до u_n число витків (заходів) черв’яка z₁ та ККД передачі η згідно з рекомендаціями [3, 5, 8]:

– якщо u_n ≤ 16, то прийняти: z₁ = 4; η = 0,87…0,92;

– якщо 16 ≤ u_n ≤ 31,5, то прийняти: z₁ = 2; η = 0,75…0,82;

– якщо u_n ≥ 31,5, то прийняти: z₁ = 1; η =0,7…0,75.

6.5. Вирахувати орієнтовну швидкість ковзання за формулою (3.91) [3, с. 87, 132]: , м/с,

де — частота обертання черв’яка, хв^–1; — крутний момент на валу черв’яч-ного колеса, Нмм.

Слід врахувати, що у формулі (3.91) крутний момент на валу колеса має розмірність у ньютон-міліметрах, а у попередніх розрахунках курсового проекту цей момент, позначений символами або (в залежності від схеми привода) і вирахуваний у ньютон-метрах (див. табл. 2.4). Це ж зауваження стосується і частоти обертання вала черв’яка, яка у попередніх розрахунках може бути позначена символами n₂ або n₃ (див. табл. 2.4).

6.6. За швидкістю ковзання визначити потрібний ступінь точності передачі [3, с. 91, табл. 3.35].

6.7. Вирахувати допустиме контактне напруження черв’ячної передачі [σ_Н]. Для передач з колесами із олов’яних бронз воно обчислюється за формулою (3.88) [3, с. 87], а для передач з колесами із твердих безолов’яних алюмінієвих бронз або чавунів за формулою [3, с. 87, табл. 3.30]:

, МПа,

де — швидкість ковзання, м/с.

6.8. Визначити допустиме напруження згину для зубів бронзового колеса при базовому числі зміни напружень для нереверсивного навантаження [3, с. 88, 132, табл. 3.31].

6.9. Обчислити сумарне число циклів зміни напружень зубів колеса при постійному навантаженні за формулою (3.85) [3, с. 86, 132]:

де — частота обертання черв’яка, хв^–1 (див. п. 6.5); — фактичний строк служби передачі, вирахуваний за формулою (3.37') [3, с. 75], годин; — номінальне передаточне число передачі (див. п. 6.3).

6.10. Вирахувати коефіцієнт довговічності черв’ячного колеса K_FL за формулою 3.93 [3, с. 88, 132]. При цьому доцільно скористатися такими зауваженнями [3, с. 88]: якщо ≤ 10⁶, його приймають рівним 10⁶ і тоді K_FL = 1; якщо
> 25·10⁷, його приймають рівним 25·10⁷ і тоді K_FL = 0,54. У випадку, якщо 10⁶ < < 25·10⁷ коефіцієнт K_FL знаходять методом логарифмування рівняння (3.93).

6.11. Вирахувати допустиме напруження згину [σ_F] для черв’ячного колеса за формулою (3.92) [3, с. 88, 132].

6.12. Визначити кількість зубів черв’ячного колеса за формулою z₂ = z₁·u_n (див. п. 6.4). Згідно з рекомендаціями (3.79) [3, с. 85]:

28 ≤ z₂ ≤ 80.

6.13. Вирахувати коефіцієнт діаметра черв’яка за формулою [3, с. 82, 132]:

,

та округлити його до найближчого більшого стандартного значення за ДСТУ 2458-94 (ГОСТ 2144-76) [3, с. 254].

6.14. Прийняти коефіцієнти, які враховують розподілення навантаження по ширині вінця колеса для випадку постійного навантаження передачі [3, с. 86, 132]:

.

6.15. Обчислити коефіцієнти, які враховують динамічне навантаження передачі за формулою (3.86) [3, с. 86, 132]:

,

де і n — визначені попередньо орієнтовна швидкість ковзання у зачепленні і ступінь точності передачі (див. пп. 6.5 і 6.6).

6.16. Вирахувати міжосьову відстань передачі із умови контактної витривалості за формулою (3.75') [3, с. 86, 132]:

, мм,

де , Нмм (див. п. 6.5); , МПа (див. п. 6.7).

6.17. Обчислити модуль зачеплення за формулою [3, с. 84, 132]:

, мм,

і округлити його до найближчого більшого стандартного значення за ГОСТ 19672-74 [3, с. 254]:

 

1-й ряд: 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0; 10,0; 12,5; 16,0; 20,0; 25,0;

2-й ряд: 1,5; 3,0; 3,5; 6,0; 7,0; 12,0.

6.18. Уточнити значення міжосьової відстані передачі відповідно до стандартного модуля за формулою (3.69) [3, с. 83, 132]:

.

6.19. Визначити ділильний кут підйому витків черв’яка за таблицею 3.22 [3, с. 83] або за формулою:

6.20. Обчислити ділильні діаметри черв’яка і колеса за формулами [3, с. 84]:

;

6.21. Визначити розрахункову швидкість ковзання у зачепленні за формулою (3.74) [3, с. 85]:

, м/с,

де — частота обертання черв’яка, хв^–1.

У випадку, якщо ця швидкість виявиться більшою, ніж попередньо визначена орієнтовна швидкість ковзання (див. п. 6.5), необхідно уточнити такі параметри:

– допустиме контактне напруження передачі за таблицею 3.30 [3, с. 87] (див. п. 6.7);

– потрібний ступінь точності за таблицею 3.35 [3, с. 91];

– коефіцієнт динамічного навантаження K'_HV за формулою (3.86) (див. п. 6.15);

– зведений кут тертя φ' при роботі бронзового колеса у парі зі стальним черв’яком за таблицею 3.25 [3, с. 85];

– ККД передачі за формулою (3.73) [3, с. 84]:

– фактичний крутний момент Т₂' на валу черв’ячного колеса за формулою (3.81) [3, с. 85, 133], врахувавши при цьому зауваження щодо позначення параметрів Т₂, N₁, n₁ (див. п. 6.5).

6.22. З метою перевірки розрахунку передачі на контактну витривалість за уточненими параметрами звичайно обчислюють уточнене значення міжосьової відстані a'_w або фактичне розрахункове контактне напруження у зачепленні за формулами відповідно (3.75') або (3.76') [3, с. 86] і порівнюють їх із раніше визначеними значеннями a_w або (див. пп. 6.18 і 6.21).

Оскільки раніше розрахунковий модуль було округлено до більшого стандартного значення (див. п. 6.17), що передбачало збільшення як міжосьової відстані a_w (див. п. 6.18), так і можливості передавання черв’ячним колесом більшого крутного моменту, доцільно спочатку перевірити співвідношення розрахункового і допустимого контактних напружень за формулою (3.76') [3, с. 86,133], тобто:

≤ .

6.23. У випадку > потрібно за методикою, викладеною у п. 3.7.10 [3, с. 88], вирахувати за формулою (3.94) уточнену розрахункову міжосьову відстань a'_w, визначити по ній новий розрахунковий модуль m', округлити його за стандартом (див. п. 6.17) і по стандартному модулю m вирахувати остаточно міжосьову відстань a_w та ділильні діаметри черв’яка d₁ і колеса d₂ (див. пп. 6.18 і 6.20).

6.24. Перевірний розрахунок зубів черв’ячного колеса на згин рекомендовано виконувати за формулою (3.77) [3, с. 86,133]:

,

де значення більшості параметрів визначені вище, зокрема: Т₂ (Нмм) — п. 6.5;
γ — п. 6.19; — п. 6.14; — п. 6.15; [σ_F] (МПа) — п. 6.11; d₂, d₁ (мм) — п. 6.20; m (мм) — п. 6.17 (у випадку уточнення значення параметрів m, d₁, d₂ — див. п. 6.23).

З метою визначення коефіцієнта форми зуба черв’ячного колеса спочатку потрібно знайти еквівалентну кількість зубів колеса за формулою (3.87) [3, с. 86, 133] (див. також п. 4.9):

,

а потім за таблицею 3.28 [3, с. 87] методом інтерполяції визначити коефіцієнт .

Звичайно черв’ячні передачі, розраховані за наведеною методикою, задовільняють умову витривалості зубів колеса при згині.

6.25. Прийняти остаточно визначені в результаті проектувального і перевірного розрахунків такі параметри передачі (рис. 6.1, а): z₁; z₂; d₁ = d_w1; d₂; a_w.

6.26. Виконати повний геометричний розрахунок черв’яка і колеса. Згідно з вимогами ЄСКД (ГОСТ 2.406-76) на кресленнях черв’яка і черв’ячного колеса та у стандартних таблицях, розміщених на цих кресленнях, потрібно вказати такі параметри зубчастих вінців (рис. 6.1, а).

На зображенні черв’яка: d_a1 [3, с. 84]; довжину нарізаної частини черв’яка b₁ [3, c. 84]; радіус кривизни перехідної кривої витка черв’яка: ρ_f1 = 0,3m; дані, які визначають контур нарізаної частини черв’яка та шорсткість бокових поверхонь витка [3, с. 115].

На зображенні черв’ячного колеса: d_a2; d_aм2; b₂ [3, с. 84]; радіус виїмки поверхні западин черв’ячного колеса (радіус вершин фрези, якою повинно бути нарізане черв’ячне колесо): R_f2 = 0,5d_a1 + 0,2m; дані, які визначають контур вінця колеса та шорсткість бокових поверхонь зубів [3, с. 144].

У таблицях параметрів зубчастого вінця черв’яка повинні бути наведені такі дані [3, с. 115]: m; z₁; вид черв’яка: ZA або Z1; ; напрям лінії витка — «правий» або «лівий» (черв’яки передач, за виключенням випадків, обумовлених кінематикою привода, повинні мати лінію правого напряму); вихідний черв’як (указати ГОСТ 19036-81); ступінь точності за ГОСТ 3675-81; ділильна товщина по хорді витка черв’яка [3, с. 107]; висота до хорди витка черв’яка [3, с. 107]; d₁; хід витка черв’яка: ; позначення креслення спряженого колеса.

Рис. 1 — Черв’ячна передача з циліндричним черв’яком
та її основні геометричні (а) і силові (б) параметри

У таблицях параметрів зубчастого вінця черв’ячного колеса повинні бути наведені такі дані [3, с. 114]: m; z₂; напрям лінії зуба; коефіцієнт зміщення черв’яка x; вихідний твірний черв’як (для стандартного твірного черв’яка указати: ГОСТ 19036-81); ступінь точності за ГОСТ 3675-81; a_w; d₂; вид спряженого черв’яка (ZA або Z1); z₁; позначення креслення спряженого черв’яка.

6.27. Вибрати мастило для охолодження редуктора. Згідно з рекомендаціями кінематична в’язкість мастила для черв’ячних передач при швидкості ковзання
υ_к = 2,5…10 м/с, середніх умовах роботи і допустимій температурі мастила 100…120° С становить ν₁₀₀ = 15…34 сСт = (15…34)·10^–6 м²/с [3, с. 116, 133].

Тому для черв’ячних редукторів, які працюють з постійним навантаженням, доцільно приймати авіаційні мастила марок МС14, МС20, МК22 за ГОСТ 21743-76, або циліндрове мастило марки 38 за ГОСТ 6411-76 [3, с. 116, 206]. Для черв’ячних редукторів, які працюють з переривами і для яких робоча температура нижче, ніж при неперервній роботі, доцільно застосовувати авіаційні мастила з меншою в’язкістю (див. вище) або індустріальні мастила марок 50, 70, 100 за ГОСТ 20799-75.

6.28. Виконати тепловий розрахунок редуктора, який для черв’ячних передач є обов’язковим [3, с. 89].

Кількість тепла, яке виділяється в редукторі під час роботи передачі:

, Дж/с,

де — потужність, яка передається черв’яком, Вт; — ККД черв’ячної передачі (див. п. 6.21).

Кількість тепла, яке віддається корпусом редуктора у навколишнє середовище:

, Дж/с,

де — коефіцієнт тепловіддачі, — при природньому охолодженні редуктора приймають ≈ 7…15 Вт/м²·град; при обдуві редуктора вентилятором, установленим на валу черв’яка, ≈ 21…28 Вт/м²·град; S = 20 a_w², м² — вільна поверхня охолодження корпуса одноступінчастого черв’ячного редуктора без врахування площі днища; = 60…90° С — температура мастила; = 20° С — температура повітря.

Якщо площа поверхні запроектованого редуктора не забезпечує нормального теплового режиму його роботи, тобто > , то рекомендується збільшити її, зробивши корпус ребристим. При цьому до загальної площі тепловіддаючої поверхні добавляють лише 50% площі ребер. Якщо застосування ребристого корпуса і штучного обдування не дають належного ефекту, то в картер редуктора можна вмонтувати змійовик з охолодною водою.

 

СПИСОК ЛІТЕРАТУРИ

 

1. Малащенко В. О., Янків В. В. Деталі машин. Курсове проектування: Навч. посібник для студентів ВНЗ. — Львів: «Новий Світ – 2000», 2004. — 232 с.

2. Коновалюк Д. М., Ковальчук Р. М., Байбула В. О., Товстушко М. М. Деталі машин. Практикум. Навчальний посібник. — К.: Кондор, 2009. — 278 с.

3. Киркач Н. Ф., Баласанян Р. А. Расчет и проектирование деталей машин: Учебное пособие для технических вузов. — 3-е изд., перераб. и доп. — Харьков: Основа, 1991. — 276 с.

4. Баласанян Р. А. Атлас деталей машин: Навч посібник для техн. вузів — Харків: Основа, 1996. — 256 с.

5. Павлище В. Т. Основи конструювання та розрахунок деталей машин: Підручник. — Львів: Афіша, 2002. — 560 с.

6. Коновалюк Д. М., Ковальчук Р. М. Деталі машин: Підручник: Друге видання. – К.: Кондор, 2004. – 584 с.

7. Проектирование механических передач: Учебно-справочное пособие для втузов/ С. А. Чернавский, Г. А. Снесарев, Б. С. Козинцев и др. – 5-е изд. перераб. и доп. – М.: Машиностроение, 1984 – 560 с.

8. Кудрявцев В. Н. Курсовое проектирование деталей машин. — Л.: Машиностроение, 1984. – 400 с.

9. Цехнович Л. И., Петриченко И. П. Атлас конструкций редукторов. — К.: Вища школа, 1990. — 151 с.

10. Иванов М. Н. Детали машин — М.: Высш. шк., 1991. — 383 с.

11. Гузенков П. Г. Детали машин. — М.: Высш. шк., 1982. — 351 с.; 1986 — 359 с.

12. Дунаев П. Ф., Леликов О. П. Конструирование узлов и деталей машин. — М.: Высш. шк., 1985 — 416 с.

13. Анурьев В. И. Справочник конструктора-машиностроителя: В 3-х т. — М.: Машиностроение, 1979 – 1989. Т1. — 728 с.; Т2. — 559 с.; Т3. — 557 с.

14. Справочник техника-конструктора. Изд. 3-е, перераб. и доп. Самохвалов Я. А., Левицкий М. Я., Григораш В. Д. Киев, «Техника», 1978. 592 с.

15. Смірнов В. М. Деталі машин. Зубчасті і черв’ячні передачі: Методичні вказівки до практичних занять. — К.: КНУБА, 2002. — 75 с.

16. Смірнов В. М. Деталі машин. Фрикційні, пасові і ланцюгові передачі: Методичні вказівки до практичних занять — К.: КНУБА, 2001. — 59 с.

17.Смірнов В. М. Вали і опори: Методичні вказівки до практичних занять для студентів спеціальності 7.090214. — К.: КНУБА, 2003. — 149 с.

18. Смірнов В. М. Деталі машин. Вибір і розрахунок муфт: Методичні вказівки до практичних занять. — К.: КНУБА, 2002. — 32 с.

19. Програмована методика нормативного проектувального розрахунку зубчастих циліндричних евольвентних передач зовнішнього зачеплення: Методичні рекомендації до практичних занять та курсового і дипломного проектування / Уклад. В. Т. Бажан. — К.: КНУБА, 2012. — 61 с.

20. Програмована методика нормативного проектувального розрахунку зубчастих конічних передач з прямими зубами Методичні рекомендації до практичних занять та курсового і дипломного проектування / Уклад. В. Т. Бажан. — К.: КНУБА, 2012. — 61 с.

21. Розробка алгоритму та програми нормативного розрахунку зубчастих циліндричних передач зовнішнього зачеплення / В. Т. Бажан, Т. В. Шевченко, Г. М. Мачишин, С. О. Лось // Гірничі, будівельні, дорожні та меліоративні машини: Всеукраїнський збірник наукових праць. — К: КНУБА, 2007, — вип. 69. — С. 82–87.

 

Додаток 1.