Корректировка (очистка) автокорреляции
Зная последствия автокорреляции, особенно отсутствие эффективности у оценок МНК, возможно, что нам понадобится исправить эту проблему. Такое исправление, зависит от знания природы зависимости нарушений друг от друга, т.е. знание о структуре автокорреляции.
Рассмотрим регрессию для двух переменных:
(1)
и будем считать, что остатки подчиняются авторегрессионной схеме первого порядка:
(2)
Теперь рассмотрим два случая: (1) значение 
коэффициента автокорреляции первого порядка известно и (2) значение не известно, но должно быть оценено.
Когда значение известно
Если коэффициент автокорреляции первого порядка известен, то проблема автокорреляции может быть легко решена. Если (1) справедливо в момент времени t, это также справедливо в момент времени 
. Следовательно,
. (3)
Умножая (3) на с обеих сторон получаем:
. (4)
Затем вычитаем выражение (4) из выражения (1)
, (5)
где 
.
Мы можем представить (5) в следующем виде:
, (6)
где 
, 
, 
, и 
.
Так как остаточный член удовлетворяет стандартным предпосылкам для применения МНК, то мы можем применить МНК для преобразованных переменных 
и 
, и получить оценки со всеми оптимальными свойствами, т.е. BLUE-оценки.
По сути, (6) равносильно использованию обобщенных наименьших квадратов (GLS). Напомним, что ОМНК ни что иное как применение МНК применительно к преобразованной модели, удовлетворяющей классическим предпосылкам применимости МНК.
Регрессия (5) известна как обобщенное или мнимое разностное уравнение.
Она включает регрессию Y по X не в первоначальном виде, а в форме разности, которая получается путем вычитания доли (= ) значения переменной в предыдущий период времени от его значения в текущий период времени.
При проведении этой процедуры мы теряем одно наблюдение, поскольку наше первое наблюдение не имеет предшествующих.
Чтобы избежать потерю этого наблюдения, его изменяют следующим образом и по Y и по X: 
и 
. Эта изменение известно как преобразование Прайса-Винсента (Prais—Winsten transformation). [1]
Когда значение неизвестно
Определение на основе Статистики Дарбина–Уотсона
Статистика Дарбина–Уотсона тесно связана с коэффициентом корреляции между соседними отклонениями через соотношение:
Преобразовав выражение, имеем:
Этот метод оценивания весьма неплох при большом числе наблюдений. В этом случае оценка параметра будет достаточно точной.
Оценивание неизвестного 
Процедура сканирования, или поиска, Хилдрета-Лу.
Так как в авторегрессионной схеме первого порядка:
предполагается, что коэффициент автокорреляции первого порядка лежит в пределах от –1 до +1, Хилдрет и Лу предложили метод систематического «сканирования» или процедуру поиска, чтобы найти его. Они рекомендуют выбирать значение между –1 и +1, используя, скажем, интервалы по 0,1 единицы и преобразуя данные с помощью обобщенного разностного уравнения (5). Таким образом, можно выбрать от 
. Для каждого выбранного рассматриваем обобщенное разностное уравнении и получаем соответствующие RSS: 
. Хилдрет и Лу предложили выбирать такое, чтобы сумма квадратов остатков была минимальной, следовательно, увеличивающей 
. Если дальнейшее уточнение необходимо, то они предлагают использовать меньшие интервалы, скажем, по 0,01 единицы, такие как 
и так далее. [1]
Пример. Рассмотрим действие процедуры Хилдрета–Лу на нашем примере, используя данные таблиц 1 и 2.
Согласно алгоритму процедуры Хилдрета–Лу, выбираем значения в пределах от –1 до +1, и для каждого значения рассчитываем сумму квадратов отклонений. Поскольку после проведения процедуры Дарбина (описана выше) нам известно, что приблизительно равен 0,9265, «просканируем» участок вблизи этого значения для выявления более точного значения , то есть найдем .
,
где , , , и .
«Сканирование» показало, что при
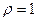
Поскольку при значение 
минимально при заданной точности, продолжаем процедуру сканирование вблизи значения 0,9 с большей точностью.
«Сканирование» показало, что при
Поскольку при значение минимально при заданной точности, продолжаем процедуру сканирование вблизи значения 0,90 с большей точностью.
«Сканирование» показало, что при
Поскольку при значение минимально при заданной точности, продолжаем процедуру сканирование вблизи значения 0,901 с большей точностью.
«Сканирование» показало, что при
Поскольку при значение минимально при заданной точности, продолжаем процедуру сканирование вблизи значения 0,9016 с большей точностью.
«Сканирование» показало, что при
Процедура сканирования Хилдрета–Лу показала, что на заданном уровне точности, значение , так как при таком значении сумма квадратов остатков минимальна, то есть коэффициент 
будет максимальным.
Оценивание неизвестного : Итеративная процедура Кохрейна—Оркатта.
Чтобы проиллюстрировать данную процедуру, рассмотрим двухфакторную модель:
(7)
и авторегрессионную схему первого порядка AR(1):
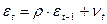, (8)
Для оценивания ρ, согласно данной процедуре, следует выполнить следующие шаги:
- Оценить (7) с помощью обычного МНК и получить, таким образом, остатки
. Следует отметить, что в модели может быть более одной объясняющей переменной X. - Используя остатки, полученные на шаге 1, построим следующую регрессию:
, (9)
которая является эмпирическим аналогом (7).
- Используя полученное в (9) значение , оценим обобщенное разностное уравнение (6).
- Поскольку, априори, неизвестно, является ли
, полученное в (9), наилучшей оценкой , заменим значение 
и 
, полученные на шаге 3, в первоначальном уравнении (7) и получим, таким образом, новые остатки 
, как
(10)
Эти остатки 
могут быть легко найдены, поскольку 
, 
, и известны.
- Далее оценим следующую регрессию:
, (11)
которая аналогична (9) и дает следующее (второе) приближение .
Поскольку мы не знаем, является ли эта вторая оценка наилучшей оценкой истинного , следует сделать следующее (третье) приближение по такому же принципу, и так далее. Вот почему, процедура Кохрейна–Оркатта называется итеративной. Но как долго нам нужно делать эти «веселые» преобразования? Основная рекомендация — заканчивать процедуру, когда очередное приближение мало отличается от предыдущего, например, менее 0,01 или 0,005. [1]
Пример. Рассмотрим действие процедуры Кохрейна–Оркатта на нашем примере, используя данные из таблиц 1 и 2.
Выполнить следующие шаги, согласно алгоритму, приведенному выше:
1. Значения остатков , полученные при оценивании регрессии (доходы — продуктивность) с помощью обычного МНК, представлены в таблице 2.
2. Используя остатки, полученные на шаге 1, построим регрессию вида (9) в программе Statistica 6.1 (рис. 10).
Рис. 10. Результаты оценивания параметров регрессии в программе Statistica 6.1
- Используя полученное в регрессии значение,
оценим обобщенное разностное уравнение вида (6). Расчеты представлены в таблице 4.
Табл. 4.
| T | Y | X |
| 
| Yt-1 | Xt-1 | ρYt-1 | ρXt-1 | Yt-ρYt-1 | Xt-ρXt-1 | 
|
| 58,5 | 47,2 | -4,81561 | — | — | — | — | — | — | — | 3,0242 | |
| 59,9 | -3,98460 | -4,81561 | 58,5 | 47,2 | 52,552 | 42,401 | 7,3478 | 5,598885 | 
| ||
| 61,7 | 49,8 | -3,46483 | -3,98460 | 59,9 | 53,81 | 43,12 | 7,8901 | 6,680222 | 0,7112 | ||
| 63,9 | 52,1 | -2,90068 | -3,46483 | 61,7 | 49,8 | 55,427 | 44,737 | 8,4731 | 7,36323 | ||
| 65,3 | 54,1 | -2,92316 | -2,90068 | 63,9 | 52,1 | 57,403 | 46,803 | 7,8968 | 7,297074 | ||
| 67,8 | 54,6 | -0,77878 | -2,92316 | 65,3 | 54,1 | 58,661 | 48,6 | 9,1391 | 6,000416 | ||
| 69,3 | 58,6 | -2,12374 | -0,77878 | 67,8 | 54,6 | 60,907 | 49,049 | 8,3933 | 9,551252 | ||
| 71,8 | -1,33072 | -2,12374 | 69,3 | 58,6 | 62,254 | 52,642 | 9,5458 | 8,357937 | |||
| 73,7 | 62,3 | -0,35534 | -1,33072 | 71,8 | 64,5 | 54,798 | 9,2 | 7,501948 | |||
| 76,5 | 64,5 | 0,87994 | -0,35534 | 73,7 | 62,3 | 66,207 | 55,966 | 10,293 | 8,534121 | ||
| 77,6 | 64,8 | 1,76656 | 0,87994 | 76,5 | 64,5 | 68,722 | 57,942 | 8,8779 | 6,857798 | ||
| 66,2 | 2,17083 | 1,76656 | 77,6 | 64,8 | 69,71 | 58,212 | 9,2897 | 7,988299 | |||
| 80,5 | 68,8 | 1,8216 | 2,1708 | 66,2 | 70,968 | 59,469 | 9,532 | 9,330639 | |||
| 82,9 | 2,65688 | 1,82160 | 80,5 | 68,8 | 72,315 | 61,805 | 10,585 | 9,194984 | |||
| 84,7 | 73,1 | 2,96326 | 2,65688 | 82,9 | 74,471 | 63,781 | 10,229 | 9,318661 | |||
| 83,7 | 72,2 | 2,60338 | 2,96326 | 84,7 | 73,1 | 76,088 | 65,668 | 7,6116 | 6,532171 | ||
| 84,5 | 74,8 | 1,55416 | 2,60338 | 83,7 | 72,2 | 75,19 | 64,859 | 9,3099 | 9,940667 | ||
| 77,2 | 2,34718 | 1,55416 | 84,5 | 74,8 | 75,909 | 67,195 | 11,091 | 10,00501 | |||
| 88,1 | 78,4 | 2,59369 | 2,34718 | 77,2 | 78,155 | 69,351 | 9,9454 | 9,049023 | |||
| 89,7 | 79,5 | 3,41132 | 2,59369 | 88,1 | 78,4 | 79,143 | 70,429 | 10,557 | 9,071029 | ||
| 79,7 | 3,56908 | 3,41132 | 89,7 | 79,5 | 80,58 | 71,417 | 9,4199 | 8,282867 | |||
| 89,7 | 79,8 | 3,19795 | 3,56908 | 79,7 | 80,85 | 71,597 | 8,8504 | 8,203201 | |||
| 89,8 | 81,4 | 2,15997 | 3,19795 | 89,7 | 79,8 | 80,58 | 71,687 | 9,2199 | 9,713368 | ||
| 91,1 | 81,2 | 3,60222 | 2,15997 | 89,8 | 81,4 | 80,67 | 73,124 | 10,43 | 8,076043 | ||
| 91,2 | 1,71074 | 3,60222 | 91,1 | 81,2 | 81,838 | 72,944 | 9,3623 | 11,05571 | |||
| 91,5 | 86,4 | 0,30376 | 1,71074 | 91,2 | 81,928 | 75,46 | 9,5724 | 10,94039 | |||
| 92,8 | 88,1 | 0,39466 | 0,30376 | 91,5 | 86,4 | 82,197 | 77,616 | 10,603 | 10,4844 | ||
| 95,9 | 90,7 | 1,64543 | 0,39466 | 92,8 | 88,1 | 83,365 | 79,143 | 12,535 | 11,55724 | ||
| 96,3 | 91,3 | 1,61869 | 1,64543 | 95,9 | 90,7 | 86,15 | 81,478 | 10,15 | 9,821585 | ||
| 97,3 | 92,4 | 1,83633 | 1,61869 | 96,3 | 91,3 | 86,509 | 82,017 | 10,791 | 10,38259 | ||
| 95,8 | 93,3 | -0,30379 | 1,83633 | 97,3 | 92,4 | 87,407 | 83,006 | 8,3926 | 10,29443 | ||
| 96,4 | 94,5 | -0,55728 | -0,30379 | 95,8 | 93,3 | 86,06 | 83,814 | 10,34 | 10,68593 | ||
| 97,4 | 95,9 | -0,55302 | -0,55728 | 96,4 | 94,5 | 86,599 | 84,892 | 10,801 | 11,00794 | ||
| -0,86910 | -0,55302 | 97,4 | 95,9 | 87,497 | 86,15 | 12,503 | 13,85028 | ||||
| 99,9 | 100,1 | -1,04023 | -0,86910 | 89,833 | 89,833 | 10,067 | 10,26713 | ||||
| 99,7 | 101,4 | -2,16484 | -1,04023 | 99,9 | 100,1 | 89,743 | 89,923 | 9,957 | 11,4773 | ||
| 99,1 | 102,2 | -3,33383 | -2,16484 | 99,7 | 101,4 | 89,563 | 91,091 | 9,5366 | 11,10947 | ||
| 99,6 | 105,2 | -4,96755 | -3,33383 | 99,1 | 102,2 | 89,024 | 91,809 | 10,576 | 13,39081 | ||
| 101,1 | 107,5 | -5,10341 | -4,96755 | 99,6 | 105,2 | 89,474 | 94,504 | 11,626 | 12,99582 | ||
| 105,1 | 110,5 | -3,23713 | -5,10341 | 101,1 | 107,5 | 90,821 | 96,57 | 14,279 | 13,92966 |
4. Поскольку, априори, неизвестно, является ли , полученное на шаге 2, наилучшей оценкой , заменим значение и , полученные на шаге 3, в первоначальном уравнении (7) и получим, таким образом, новые остатки , как . Результаты шага 4 представлены в таблице 5.
Табл. 5.
| T | Y | X |
|
| 
|
| 58,5 | 47,2 | 3,024217 | 21,90523 | ||
| 59,9 |
| 22,73624 | 21,90523 | ||
| 61,7 | 49,8 | 0,711241 | 23,256 | 22,73624 | |
| 63,9 | 52,1 | 23,82015 | 23,256 | ||
| 65,3 | 54,1 | 23,79767 | 23,82015 | ||
| 67,8 | 54,6 | 25,94205 | 23,79767 | ||
| 69,3 | 58,6 | 24,59709 | 25,94205 | ||
| 71,8 | 25,39011 | 24,59709 | |||
| 73,7 | 62,3 | 26,3655 | 25,39011 | ||
| 76,5 | 64,5 | 27,60077 | 26,3655 | ||
| 77,6 | 64,8 | 28,4874 | 27,60077 | ||
| 66,2 | 28,89166 | 28,4874 | |||
| 80,5 | 68,8 | 28,54243 | 28,89166 | ||
| 82,9 | 29,3777 | 28,54243 | |||
| 84,7 | 73,1 | 29,6841 | 29,3777 | ||
| 83,7 | 72,2 | 29,32422 | 29,6841 | ||
| 84,5 | 74,8 | 28,27499 | 29,32422 | ||
| 77,2 | 29,06801 | 28,27499 | |||
| 88,1 | 78,4 | 29,31452 | 29,06801 | ||
| 89,7 | 79,5 | 30,13216 | 29,31452 | ||
| 79,7 | 30,28991 | 30,13216 | |||
| 89,7 | 79,8 | 29,91879 | 30,28991 | ||
| 89,8 | 81,4 | 28,8808 | 29,91879 | ||
| 91,1 | 81,2 | 30,32305 | 28,8808 | ||
| 91,2 | 28,43158 | 30,32305 | |||
| 91,5 | 86,4 | 27,0246 | 28,43158 | ||
| 92,8 | 88,1 | 27,11549 | 27,0246 | ||
| 95,9 | 90,7 | 28,36627 | 27,11549 | ||
| 96,3 | 91,3 | 28,33952 | 28,36627 | ||
| 97,3 | 92,4 | 28,55716 | 28,33952 | ||
| 95,8 | 93,3 | 26,41704 | 28,55716 | ||
| 96,4 | 94,5 | 26,16355 | 26,41704 | ||
| 97,4 | 95,9 | 26,16782 | 26,16355 | ||
| 25,85173 | 26,16782 | ||||
| 99,9 | 100,1 | 25,68061 | 25,85173 | ||
| 99,7 | 101,4 | 24,55599 | 25,68061 | ||
| 99,1 | 102,2 | 23,387 | 24,55599 | ||
| 99,6 | 105,2 | 21,75328 | 23,387 | ||
| 101,1 | 107,5 | 21,61743 | 21,75328 | ||
| 105,1 | 110,5 | 23,4837 | 21,61743 |
5. Используя остатки , полученные на шаге 4, построим регрессию вида (9) в программе Statistica 6.1 (рис. 11).
Рис. 11. Результаты оценивания параметров регрессии в программе Statistica 6.1
Таким образом, получено второе приближение 
. Повторяя шаги 1–5, было получено третье приближение . Поскольку третье приближение ничем не отличается от второго, то нет смысла продолжать процедуру Кохрейна–Оркатта. Следовательно, примем значение как конечное оцененное значение.
Теперь проверим на наличие автокорреляции, преобразованное с помощью полученного , уравнение регрессии вида (6). Используя колонки 10 и 11, таблицы 4 построим, с помощью программы Statistica 6.1 регрессию 
по 
. Расчеты представлены на рис. 12 и в таблице 6.
Рис. 12. Результаты оценивания параметров регрессии в программе Statistica 6.1
Табл. 6.
| 
|
| 
| 
| 
|
| — | — | — | — | — | — |
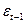
| 7,3478 | 5,598885 | -0,48431 | — | — | — |
| 7,8901 | 6,680222 | -0,49743 | -0,48431 | 0,00017212 | 0,24743 |
| 8,4731 | 7,36323 | -0,26526 | -0,49743 | 0,05389966 | 0,07036 |
| 7,8968 | 7,297074 | -0,80760 | -0,26526 | 0,29413354 | 0,65222 |
| 9,1391 | 6,000416 | 1,10080 | -0,80760 | 3,64200735 | 1,21176 |
| 8,3933 | 9,551252 | -1,46901 | 1,10080 | 6,60390802 | 2,15798 |
| 9,5458 | 8,357937 | 0,29648 | -1,46901 | 3,11694152 | 0,08790 |
| 9,2 | 7,501948 | 0,39036 | 0,29648 | 0,00881357 | 0,15238 |
| 10,293 | 8,534121 | 0,95333 | 0,39036 | 0,31693646 | 0,90884 |
| 8,8779 | 6,857798 | 0,39910 | 0,95333 | 0,30717156 | 0,15928 |
| 9,2897 | 7,988299 | 0,23023 | 0,39910 | 0,0285187 | 0,05300 |
| 9,532 | 9,330639 | -0,21696 | 0,23023 | 0,19997827 | 0,04707 |
| 10,585 | 9,194984 | 0,90523 | -0,21696 | 1,25930725 | 0,81943 |
| 10,229 | 9,318661 | 0,48571 | 0,90523 | 0,17599577 | 0,23591 |
| 7,6116 | 6,532171 | -0,69993 | 0,48571 | 1,4057294 | 0,48990 |
| 9,3099 | 9,940667 | -0,75247 | -0,69993 | 0,00276023 | 0,56620 |
| 11,091 | 10,00501 | 0,99582 | -0,75247 | 3,0564945 | 0,99165 |
| 9,9454 | 9,049023 | 0,34107 | 0,99582 | 0,42869861 | 0,11633 |
| 10,557 | 9,071029 | 0,94160 | 0,34107 | 0,36064169 | 0,88661 |
| 9,4199 | 8,282867 | 0,20914 | 0,94160 | 0,53650615 | 0,04374 |
| 8,8504 | 8,203201 | -0,31944 | 0,20914 | 0,27939343 | 0,10204 |
| 9,2199 | 9,713368 | -0,72568 | -0,31944 | 0,16503061 | 0,52661 |
| 10,43 | 8,076043 | 1,32554 | -0,72568 | 4,20752154 | 1,75707 |
| 9,3623 | 11,05571 | -1,27287 | 1,32554 | 6,75175532 | 1,62020 |
| 9,5724 | 10,94039 | -1,00347 | -1,27287 | 0,07257852 | 1,00694 |
| 10,603 | 10,4844 | 0,26127 | -1,00347 | 1,5995488 | 0,06826 |
| 12,535 | 11,55724 | 1,64235 | 0,26127 | 1,90737727 | 2,69730 |
| 10,15 | 9,821585 | 0,14909 | 1,64235 | 2,22979974 | 0,02223 |
| 10,791 | 10,38259 | 0,50159 | 0,14909 | 0,12425223 | 0,25159 |
| 8,3926 | 10,29443 | -1,85146 | 0,50159 | 5,53681089 | 3,42789 |
| 10,34 | 10,68593 | -0,10507 | -1,85146 | 3,04986336 | 0,01104 |
| 10,801 | 11,00794 | 0,19053 | -0,10507 | 0,08737765 | 0,03630 |
| 12,503 | 13,85028 | 0,43215 | 0,19053 | 0,05838254 | 0,18676 |
| 10,067 | 10,26713 | -0,16292 | 0,43215 | 0,35411152 | 0,02654 |
| 9,957 | 11,4773 | -0,89472 | -0,16292 | 0,53553417 | 0,80053 |
| 9,5366 | 11,10947 | -1,12611 | -0,89472 | 0,05354133 | 1,26813 |
| 10,576 | 13,39081 | -1,25899 | -1,12611 | 0,0176555 | 1,58505 |
| 11,626 | 12,99582 | -0,00525 | -1,25899 | 1,57184206 | 0,00003 |
| 14,279 | 13,92966 | 2,16756 | -0,00525 | 4,72111522 | 4,69831 |
| 55,1221061 | 29,99083 |
Для проверки успешности проведенной операции по очистке регрессии от автокорреляции рассчитаем статистику Дарбина—Уотсона:
.
Из таблицы, представленной на рисунке 10, найдем значения верхней и нижней границы. Для нашего примера 
, 
, поэтому:
Поскольку 
, можно сделать вывод об отсутствии автокорреляции остатков. Следовательно, очистка остатков регрессии от автокорреляции прошла успешно.
Стоит также обратить внимание на изменение коэффициентов и значений t- и F-статистик в первоначальной регрессии (доход—продуктивность), рис. 8 и преобразованной регрессии, рис. 12. Можно заметить, что данные характеристики регрессии уменьшились. Но, несмотря на ухудшение качества модели, были получены оценки регрессии со всеми оптимальными свойствами, т.е. BLUE-оценки.
Список литературы