Понятие автокорреляции случайной составляющей

Структура работы

Понятие автокорреляции случайной составляющей. 2

Экономические причины автокорреляции: инерция экономических показателей, предварительная обработка первичных данных, «паутинообразный эффект», кажущаяся автокорреляция при не включении в модель существенной переменной 5

Последствия неучета автокорреляции для свойств оценок коэффициентов регрессии, полученных по МНК.. 9

Графическое диагностирование автокорреляции. Тест серий. 10

Тест серий (runs test) 15

Модель авторегрессии ошибок первого порядка (марковская схема) 18

Тесты на автокорреляцию остатков: критерий Дарбина-Уотсона. 20

Условия применимости статистики Дарбина-Уотсона для диагностирования автокорреляции: наличие в модели свободного члена, отсутствие лаговых переменных, первый порядок авторегрессионной схемы. 26

Тест Бреуша—Годфри. 27

Оценивание регрессии в условиях автокорреляции остатков: процедуры Кохрейна-Орката, Хилдрета-Лу. 28

Список литературы.. 42

Понятие автокорреляции случайной составляющей

Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений 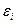от значений отклонений во всех других наблюдениях. Отсутствие зависимости гарантирует отсутствие коррелированности между любыми отклонениями 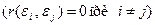и, в частности, между соседними отклонениями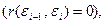 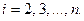(Третье условие Гаусса-Маркова)

Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные данные).

Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов. При использовании перекрестных данных наличие автокорреляции (пространственной корреляции) крайне редко. В силу этого в дальнейших выкладках вместо символа i порядкового номера наблюдения будем использовать символ t, отражающий момент наблюдения. Объем выборки при этом будем обозначать символом вместо n.

Рассмотрим уравнение регрессии вида

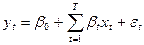
Для каждого момента (периода) времени 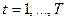значение компоненты , определяется как

или

Рассматривая последовательность остатков как временной ряд, можно построить график их зависимости от времени. В соответствии с предпосылками МНК остатки , должны быть случайными (рис. 1 а)). Однако при моделировании временных рядов нередко встречается ситуация, когда остатки содержат тенденцию (рис. 1 б) и в)) или циклические колебания (рис. 1 г)). Это свидетельствует о том, что каждое следующее значение остатков зависит от предшествующих. В этом случае говорят о наличии автокорреляции остатков.

Рис. 1

Причем, в экономических задачах значительно чаще встречается так называемая положительная автокорреляция 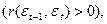нежели отрицательная автокорреляция

Чаще всего положительная автокорреляция вызывается направленным постоянным воздействием некоторых не учтенных в модели факторов. Суть автокорреляции поясним следующим примером. Пусть исследуется спрос Y на прохладительные напитки от дохода X по ежемесячным данным. Трендовая зависимость, отражающая увеличение спроса с ростом дохода, может быть представлена линейной функцией 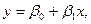изображенной на рис. 2.

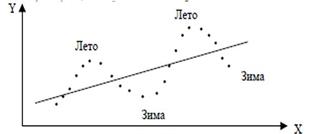
Рис.2

Однако фактические точки наблюдений обычно будут превышать трендовую линию в летние периоды и будут ниже ее в зимние.

Аналогичная картина может иметь место в макроэкономическом анализе с учетом циклов деловой активности.

Отрицательная автокорреляция фактически означает, что за положительным отклонением имеет место отрицательное и наоборот. Возможная схема рассеивания точек в этом случае представлена на рис.

Рис. 3

Такая ситуация может иметь место, например, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима – лето). [2]

Среди основных причин, вызывающих появление автокорреляции, можно выделить ошибки спецификации, инерцию в изменении экономических показателей, эффект паутины, сглаживание данных.

Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводит к системным отклонениям точек наблюдений от линии регрессии, что может привести к автокорреляции.

Проиллюстрируем это следующим примером. Анализируется зависимость предельных издержек МС от объема выпуска Q. Если для ее описания вместо реальной квадратичной модели 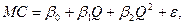выбрать линейную модель то совершается ошибка спецификации. Ее можно рассматривать как неправильный выбор формы модели или как отбрасывание значимой переменной при линеаризации указанных моделей. Последствия данной ошибки выразятся в системном отклонении точек наблюдений от прямой регрессии (см. рис. 4) и существенном преобладании последовательных отклонений одинакового знака над соседними отклонениями противоположных знаков. Налицо типичная картина, характерная для положительной автокорреляции.

Рис. 4

Инерция. Многие экономические показатели (например, инфляция, безработица, ВНП и т. п.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Действительно, экономический подъем приводит к росту занятости, сокращению инфляции, увеличению ВНП и т. д. Этот рост продолжается до тех пор, пока изменение конъюнктуры рынка и ряда экономических характеристик не приведет к замедлению роста, затем остановке и движению вспять рассматриваемых показателей. В любом случае эта трансформация происходит не мгновенно, а обладает определенной инертностью.

Эффект паутины. Во многих сферах экономики экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом). Например, предложение сельскохозяйственной продукции реагирует на изменение цены с запаздыванием (равным периоду созревания урожая). Большая цена сельскохозяйственной продукции в прошлом году вызовет (скорее всего) ее перепроизводство в текущем году, а следовательно, цена на нее снизится и т. д. В этой ситуации нельзя предполагать случайность отклонений друг от друга.

Рис. 5

Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его подынтервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что, в свою очередь, может послужить причиной автокорреляции. [2]

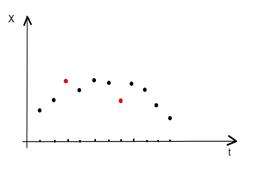
Рис. 6