Проверка гипотезы о законе распределения

 

Цель работы – освоение методики проверки гипотезы о нормальном законе распределения с использованием инструментов статистического анализа MS Excel.

Проверка гипотез состоит в следующем. Рассмотрим две гипотезы о законе распределения.

Основная гипотеза H₀ : F(x) = N(a,b²) -имеет место нормальное распределение с математическим ожиданием aи дисперсией b² и

альтернативная гипотеза H₁ : F(x)≠ N(a,b²) -закон распределения отличается от нормального распределения N(a,b²).

По результатам эксперимента нужно заключить, согласуются ли они с основной гипотезой H₀ . Для этого числовую ось (-∞,+∞) разделим на k интервалов точками z_i:

.

 

Пусть все интервалы, кроме первого и последнего, имеют одинаковую длину:

,

Значение 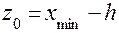. Вычислим эмпирические частоты n_i :число значений выборки в данном интервале. Из построения следует, что для бесконечных интервалов n_i = 0. Вычислим вероятность попадания в каждый интервал (z_i ,z_i+1] в предположении, что верна гипотеза H₀

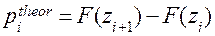
Тогда вероятность попадания значений выборки в данный интервал. Мерой расхождения между эмпирическими и теоретическими частотами служит критерий согласия Пирсона

где - относительная частота.

При n→∞ эта величина стремится к распределению Пирсона с (k-3) степенями свободы. Правило принятия гипотезы состоит в следующем.

1) Вычислить наблюдаемое значение ,

2) Выбрать уровень значимости критерия α (α=0,05) и по таблицам χ²

найти квантиль . Уровень значимости критерия α – вероятность ошибочно отвергнуть гипотезу H₀.

3) Если 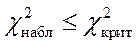, то основная гипотеза H₀ не противоречит наблюдениям. Если , то основная гипотеза H₀ отвергается.