Пример 2.
Построить автомат, который допускает язык L = {w|w} , содержащий четное число 0 и 1.
Решение.
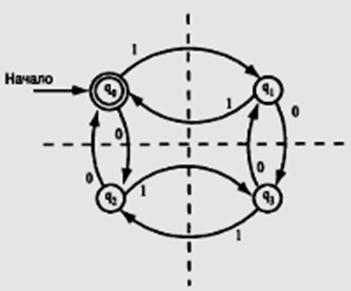
Выделим 4 состояния, запоминающих четное и нечетное число 0 и 1:

Состояние q0 одновременно допускающее и начальное, т. к. 0 – четное число.
Определение. Регулярный язык для некоторого автомата – это множество цепочек, приводящих автомат из начального состояния в одно из допускающих.
Например, для первого автомата язык - множество цепочек из 0 и 1, содержащих подцепочку 01, для второго автомата язык - множество цепочек из 0 и 1, содержащих четное число 0 и четное число 1.
Таким образом, язык: множество цепочек из 0 и 1, содержащих подцепочку «01» - можно задать распознающим автоматом А01 = (Q,S,d,q0,F), где Q={q0,q1,q2}; S={0,1}; d - таблица или диаграмма переходов (см. выше); q0 – начальное состояние; F={q1} – множество заключительных состояний.
Язык L = {w|w}, содержащий четное число 0 и 1 можно задать распознающим автоматом АL = (Q,S,d,q0,F), где Q={q0,q1,q2,q3}; S={0,1}; d - диаграмма переходов (см. выше); q0 – начальное состояние; F={q0} – множество заключительных состояний.
Задать язык, содержащий подцепочку «000» распознающим конечным автоматом.