Бинарные отношения

ДМ. Лекция №

Тема: «Отношения»

 

Def: N-местным отношением P на множествах A₁, A₂ … A_n называется любое подмножество декартового произведения A₁ × A₂ × …× A_n.

При n = 1 отношение P называется унарным (одноместным) и является подмножеством множества A₁. При n = 2 отношение называется бинарным (или двуместным) и является подмножеством декартового произведения A₁ × A₂.

Бинарные отношения

Вообще бинарным отношением называется любое множество упорядоченных пар. Если P – бинарное отношение и 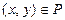, то говорят, что элемент х находится в отношении P к элементу у, или что для элементов х и у выполняется отношение Р, или что х и у связаны отношением Р. Вместо записи 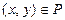часто используют более простую – .

Def: Областью определения бинарного отношения P называется множество всех первых элементов упорядоченных пар, входящих в это отношение:

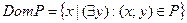
Def: Областью определения бинарного отношения P называется множество всех вторых элементов упорядоченных пар, входящих в это отношение:

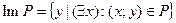
Если 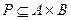, то говорят, что Р есть отношение между элементами множеств А и В или что Р определено на паре множеств А и В.

Def:Если 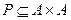(декартов квадрат), то говорят, что Р есть бинарное отношение на множестве А.

Def: Для любого множества А отношение 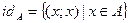называется тождественным отношением или диагональю, а 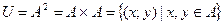- полным отношением или полным квадратом.

Def:Два отношения Р и S называются равными (Р=S), если для любых х, у 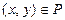тогда и только тогда, когда 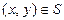, то есть Р и S равны как множества.

Пример 1.На паре множеств 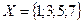и 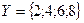определено отношение 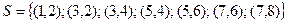. Показать, что 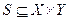, указать область определения и область значения этого отношения.

Решение.