Тема 3. Формула полной вероятности.

Требуется определить вероятность некоторого события 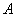, которое может произойти вместе с одним из событий:

,

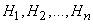образующих полную группу несовместных событий. Будем эти события называть гипотезами.

Докажем, что в этом случае

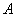, т.е. вероятность события вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе.

Формула (3.4.1) носит название формулы полной вероятности.

 

Доказательство.

Так как гипотезы 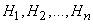образуют полную группу, то событие 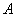может появиться только в комбинации с какой-либо из этих гипотез:

.

Так как гипотезы 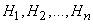несовместны, то и комбинации также несовместны; применяя к ним теорему сложения, получим:

.

Применяя к событию теорему умножения, получим:

, что и требовалось доказать.

Определение. Пусть событие А может произойти только совместно с одним из событий Н₁, Н₂,…, Н_п, образующих полную группу несовместных событий. Тогда события Н₁, Н₂,…, Н_п называются гипотезами.

 

Теорема. Вероятность события А, наступающего совместно с гипотезами Н₁, Н₂,…, Н_п, равна:

(3.1)

где p(H_i) – вероятность i- й гипотезы, а p(A/H_i) – вероятность события А при условии реализации этой гипотезы. Формула (3.1) носит название формулы полной вероятности.

Доказательство.

Можно считать событие А суммой попарно несовместных событий АН₁, АН₂,…, АН_п. Тогда из теорем сложения и умножения следует, что

что и требовалось доказать.

Пример. Имеются три одинаковые урны с шарами. В первой из них 3 белых и 4 черных шара, во второй – 2 белых и 5 черных, в третьей – 10 черных шаров. Из случайно выбран-ной урны наудачу вынут шар. Найти вероятность того, что он белый.

Решение. Будем считать гипотезами Н₁, Н₂ и Н₃ выбор урны с соответствующим номером. Так как по условию задачи все гипотезы равновозможны, то 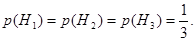Найдем условную вероятность А при реализации каждой гипотезы: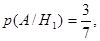

Тогда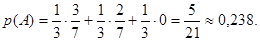

 

 

Пример. Имеются три одинаковые на вид урны; в первой урне два белых и один черный шар; во второй – три белых и один черный; в третьей – два белых и два черных шара. Некто выбирает наугад одну из урн и вынимает из нее шар. Найти вероятность того, что этот шар белый.

Решение. Рассмотрим три гипотезы:

- выбор первой урны,

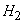- выбор второй урны,

- выбор третьей урны

и событие 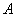– появление белого шара.

Так как гипотезы, по условию задачи, равновозможные, то

.

Условные вероятности события 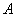при этих гипотезах соответственно равны:

.

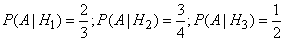По формуле полной вероятности

.

Пример 2. По самолету производится три одиночных выстрела. Вероятность попадания при первом выстреле равна 0,4, при втором – 0,5, при третьем 0,7. Для вывода самолета из строя заведомо достаточно трех попаданий; при одном попадании самолет выходит из строя с вероятностью 0,2, при двух попаданиях – с вероятностью 0,6. Найти вероятность того, что в результате трех выстрелов самолет будет выведен из строя.

Тема 4. Теорема Гипотез. (Формула Байесса)

Следствием теоремы умножения и формулы полной вероятности является так называемая теорема гипотез, или формула Бейеса.

Имеется полная группа несовместных гипотез . Вероятности этих гипотез до опыта известны и равны соответственно . Произведен опыт, в результате которого наблюдено появление некоторого события 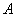. Спрашивается, как следует изменить вероятности гипотез в связи с появлением этого события?

Здесь, по существу, речь идет о том, чтобы найти условную вероятность 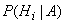для каждой гипотезы.

Из теоремы умножения имеем:

,

или, отбрасывая левую часть,

,

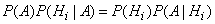
откуда

.

Выражая 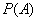с помощью формулы полной вероятности , имеем:

 

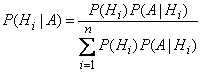
Формула носит название формулы Бейеса или теоремы гипотез.