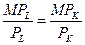Long Run Production

The long run production function is multidimensional, two or more inputs and output changes. If there are 2 inputs and one output, the long run production relationship is 3 dimensional. Using a topological map of "isoquants," three dimensions can be shown in two dimensions.

 

У

E Q₃

Q₂

Q₁

0 Х

 

Figure is a representation of a long run production model using isoquants and isocosts. This model is an attempt to represent a threedimensional model in two dimensions. It can be thought of as a “topological map” of production. In Figure, two different levels of output of the good are shown. The term “isoquant” means equal quantity. In the graph two isoquants are shown. Q1 and Q2 represent two different levels of output. There are an infinite number of isoquants, one for each possible level of output but only two are shown. The isoquant (Q1) represents all combinations of labour (L) and capital (K) that will produce Q1 amount of output. Three input combinations that will produce Q1 output are identified in the graph (points J, B and H). while there are an infinite number of input combinations that lie along the isoquant (Q1), only these three are marked.

Isoquant Q2 is a larger output than Q1. Only input combination LA, KA at point A is identified.

 

К

ТС/Р_к

ТС

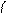α

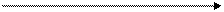0 ТС/Р_L L

ТС = L×Р_L + K×Р_K

ТС = L×w + K×r

 

Two isocost functions are also shown in Figure. These are TC1 and TC2. “Isocost” means equal cost. All output combinations that lie on TC1 require the same expenditure. All output combinations that cost less than TC1 lie inside the isocost. Output combinations that cost more than TC1 lie outside the isocost. TC2 represents a greater cost than TC1. The isocost function can be located by finding the intercepts on the K-axis (capital axis) and L-axis (labour axis). The L-intercept is found by dividing the total cost (TC1 by the price of labour.

Q1 output could be produced by using KA capital and LJ labour (point J on Q1). Point H (LA labour and KH capital will also result in Q1 output. Notice that both points J and H lie outside the isocost TC1. Since point B lies on TC1, that input combination cost less than those at point J and H. If Q1 output is desired, TC1 is the lowest cost of production that can be attained. This is accomplished by using LB labour and KB capital.

The lowest cost of producing Q2 given the price of labour and capital is at point A.

The slope of the isoquant represents the rate at which one input can be substituted for another and still produce the same output. The slope of the isocost represents relative price so of the inputs. The lowest cost combination of inputs is at the point of tangency between the isocost and the isoquant. When the isocost function is tangent to an isoquant, it identifies the combination of inputs that minimizes the cost per unit for that level of output.

 

MRTS_LK = - tg γ = или .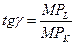

 

The short-run production relationships are cross-sections taken out of the isoquant map. In intermediate microeconomics you will study the cost and production relationships in the isoquant map.

 

K

TC/P_K Q₁

Q₄

E Q₃

Q₂

α

0 TC/P_L L