Абсолютная, относительная погрешности

Измерения многих величин, встречающихся в природе, не может быть точным. Измерение дает число, выражающее величину с той или иной степенью точности (измерение длины с точностью до 0,01 см, вычисление значения функции в точке с точностью до 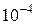и т.д.), то есть приближенно, с некоторой погрешностью. Погрешность может быть задана наперед, или, наоборот, ее требуется найти.

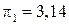Теория погрешностей имеет объектом своего изучения в основном приближенные числа. При вычислениях вместо обычно используют приближенные числа: (если точность не особо важна), 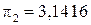(если точность важна). Как проводить вычисления с приближенными числами, определять их погрешности – этим занимается теория приближенных вычислений (теория погрешностей).

В дальнейшем точные числа будем обозначать заглавными буквами 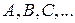, а соответствующие им приближенные – строчными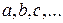

Погрешности, возникающие на том или ином этапе решения задачи можно условно разделить на три типа:

1) Погрешность задачи. Этот тип погрешности возникает при построении математической модели явления. Далеко не всегда оказывается возможным учесть все факторы и степень их влияния на окончательный результат. То есть, математическая модель объекта не является его точным образом, не является точным его описание. Такая погрешность является неустранимой.

2) Погрешность метода. Эта погрешность возникает в результате подмены исходной математической модели более упрощенной, например, в некоторых задачах корреляционного анализа приемлемой является линейная модель. Такая погрешность является устранимой, так как на этапах вычисления она может свестись к сколь угодно малой величине.

3) Вычислительная («машинная») погрешность. Возникает при выполнении арифметических операций компьютером.

Определение 1.1. Пусть 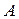– точное значение величины (числа), 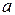– приближенное значение той же величины ( 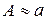). Истинной абсолютной погрешностью приближенного числа 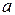называется модуль разности точного и приближенного значений:

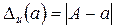. (1.1)

Пусть, например, 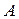=1/3. При вычислении на МК дали результат деления 1 на 3 как приближенное число 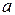=0,33. Тогда .

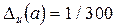Однако в действительности в большинстве случаев точное значение величины не известно, а значит, нельзя применять (1.1), то есть нельзя найти истинную абсолютную погрешностью. Поэтому вводят другую величину, служащей некоторой оценкой (верхней границей для ).

Определение 1.2. Предельной абсолютной погрешностью 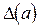приближенного числа 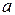, представляющее неизвестное точное число 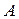, называется такое возможно меньшее число, которого не превосходит истинная абсолютная погрешность , то есть 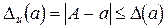. (1.2)

Для приближенного числа 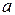величин 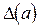, удовлетворяющих неравенству (1.2), существует бесконечно много, но самым ценным из них будет наименьшее из всех найденных. Из (1.2) на основании определения модуля имеем 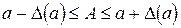, или сокращенно в виде равенства

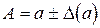. (1.3)

Равенство (1.3) определяет границы, в которых находится неизвестное точное число 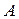(говорят, что приближенное число 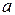выражает точное 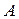с предельной абсолютной погрешностью). Нетрудно видеть, что чем меньше 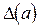, тем точнее определяются эти границы.

Например, если измерения некоторой величины дали результат 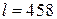см, при этом точность этих измерений не превосходила 1 см, то истинная (точная) длина см.

Пример 1.1. Дано число 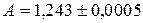. Найти предельную абсолютную погрешность числа 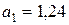числом .

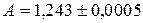Решение: Из равенства (1.3) для числа 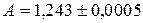( 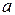=1,243; 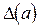=0,0005) имеем двойное неравенство 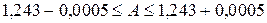, то есть

(*)

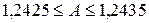Тогда задача ставится так: найти для числа 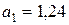предельную абсолютную погрешность , удовлетворяющую неравенству 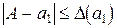. Учитывая условие (*), получим (в (*) вычитаем 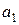из каждой части неравенства)

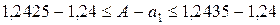Так как в нашем случае 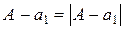, то 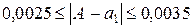, откуда =0,0035.

Ответ: =0,0035.

Предельная абсолютная погрешность часто плохо дает представление о точности измерений или вычислений. Например, 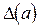=1 м при измерениях длины здания укажет, что они проводились не точно, а та же погрешность 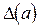=1 м при измерениях расстояния между городами дает очень качественную оценку. Поэтому вводят другую величину.

Определение 1.3. Истинной относительной погрешностью 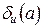числа 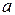, являющегося приближенным значением точного числа 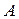, называется отношение истинной абсолютной погрешности числа 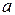к модулю самого числа :

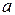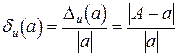. (1.4)

Например, если 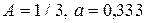соответственно точное и приближенное значения, то

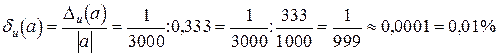Однако формула (1.4) неприменима, если не известно точное значение числа. Поэтому по аналогии с предельной абсолютной погрешностью вводят предельную относительную погрешность.

Определение 1.4. Предельной относительной погрешностью числа 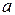, являющегося приближенным значением неизвестного точного числа 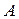, называется возможно меньшее число 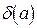, которого не превосходит истинная относительная погрешность 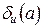, то есть

. (1.5)

Из неравенства (1.2) имеем 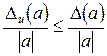; откуда, учитывая (1.5)

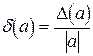. (1.6)

Формула (1.6) имеет большую практическую применимость по сравнению с (1.5), так как в ней не участвует точное значение. Учитывая (1.6), (1.3), можно найти границы, в которых заключается точное значение неизвестной величины:

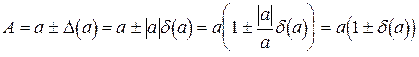
(приближенное число 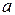выражает неизвестное точное число 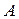с предельной относительной погрешностью 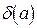). Ясно, что чем меньше 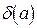, тем точнее вычисляются границы точного числа .

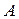Пример 1.2. Учитывая данные примера 1.1, найти .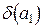

Решение: Имеем =0,0035, 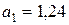. Тогда 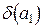= 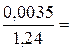0,0028.

Пример 1.3. Выяснить, какое из приближенных равенств точнее:

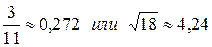Решение:Для решения задачи необходимо найти предельные относительные погрешности чисел 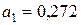( 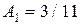), 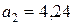( ) и сравнить их.

1) Находим сначала предельные абсолютные погрешности. При помощи калькулятора вычисляем числа 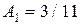, с большим числом знаков: 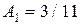=0,2727(27), =4,2426.... Тогда имеем (по определению)

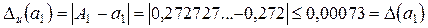2) Теперь вычисляем предельные относительные погрешности, пользуясь формулой (1.6):

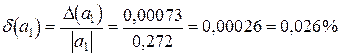Итак, 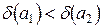. Значит, первое равенство точнее второго.