Система с неограниченным временем ожидания.

Марковские процессы в многоканальной

Системе с ожиданием

Система с неограниченным временем ожидания.

Цель работы: Исследование характеристики марковских процессов при каналах обработки заявок с неограниченной и ограниченной очередью заявок.

Исходные данные:

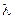
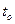
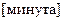
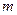
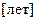
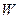
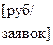
№					А
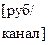
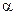
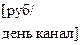
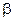
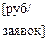
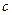
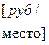
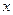
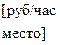
		0.72	2.6

 

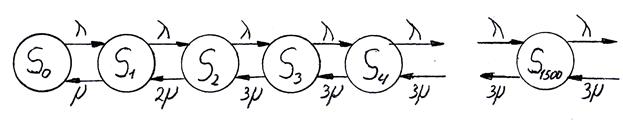
Граф состояния многоканальной системы с неограниченным временем ожидания.

 

Из графа состояния многоканальной системы составляем дифференциальные уравнения Колмогорова. Имеем:

 

 

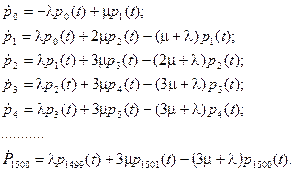
Средняя длина очереди определяется по формуле:

,

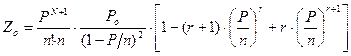где - среднее число заявок, поступающих в систему за время обслуживания одной заявки;

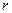- максимальная длина очереди.

Среднее время ожидания в очереди со средней длиной очереди:

.

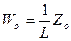Среднее число заявок в системе:

.

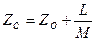Среднее число пребывания в системе:

.

Прибыль в зависимости от числа каналов выражается в следующем виде:

,

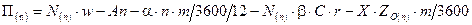где 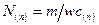- число заявок в n – канальной системе за все время работы;

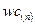- среднее время пребывания в системе.

 

Алгоритм решения системы в MATLAB

 

L=40/3600; to=0.732*60; % приведение к масштабу в секундах

M=1/to; dt=5e0; t=[0:dt:5000*dt]';

u=1e-12+1e-12*sin(t/5);

m=2.7*365*12*3600; %[c]– планируемый срок эксплуатации системы

w=122; %[руб/заявка] – прибыль от обслуженной заявки

A=157000; %[руб/ канал] – инвестиции в 1 канал

a=5700; %[руб/день ?канал] – экспл.затраты на 1 канал в день

b=102; %[руб/заявка] – текущие экспл.расходы на 1 заявк

C=7400; %[руб/место] - инвестиции в 1 место очереди

X=2600; %[руб/час/место] – экспл.затраты на поддерж.1 места в очереди

r=7; %максимальное число заявок в очереди

n=3; %количество каналов системы

p=L*to; %приведенная интенсивность потока заявок

while n<9

sm=1+p^(n+1)/factorial(n)/(n-p);

for i=1:n sm=sm+p^(i)/factorial(i); end

p0(n)=1/sm; %вероятность начального состояния So

for i=1:n P(i,n)=p0(n)*p^i/factorial(i);end %вероятностb состояний Sj

z(i+1)=P(i,n);

%for i=n+1:n+r P(i,n)=p0(n)*p^(i)/factorial(n)/n^(i-n); end

for i=n+1:n+r P(i,n)=p0(n)*p^(i)/factorial(n)/n^(i-n); end

zo(n)=P(n,n)*p/n/(1-p/n)^2 %средняя длина очереди

ver(n)=p0(n); for i=1:n+r ver(n)=ver(n)+P(i,n);end%суммарная вероятность

zc(n)=zo(n)+p %среднее число заявок в системе

wc(n)=zc(n)/L %[сек] - среднее время пребывания заявки в системе

wo(n)=zo(n)/L %[сек] - среднее время пребывания заявки в очереди

N(n)=m/wc(n); %число заявок в n-канальной системе за все время

Pr(n)=N(n)*(w-b)-(A+a*m/3600/12)*n-X*zo(n)*m/3600-C*r %прибыль

%if Pr(n)<0 pr(n)=-log(-Pr(n)); else pr(n)=log(Pr(n));end;

n=n+1;

end

t1=[1:1:8];

figure(1); plot(t1,Pr,'b','LineWidth',3),grid;

figure(2); plot(t1,wc,'b','LineWidth',3),grid;

nm=1;Prmax=Pr(1);for i=1:n-1 if Pr(i)>Prmax Prmax=Pr(i);nm=i;end;end

Wmin=((A+a*m/3600/12)*nm+X*zo(nm)*m/3600+C*r+N(nm)*b)/N(nm); Wmin%миним стоим обслуж заявки

 

zo =

 

0 0 0.0028 0.0002 0.0000 0.0000 0.0000 0.0000

 

 

zc =

 

0 0 0.4908 0.4882 0.4880 0.4880 0.4880 0.4880

 

 

wc =

 

0 0 44.1681 43.9407 43.9215 43.9201 43.9200 43.9200

 

 

wo =

 

0 0 0.2481 0.0207 0.0015 0.0001 0.0000 0.0000

 

 

Pr =

 

1.0e+007 *

 

0 0 0.1818 -0.3778 -0.9538 -1.5311 -2.1085 -2.6860

 

Wmin =

 

120.1135

прибыль

n

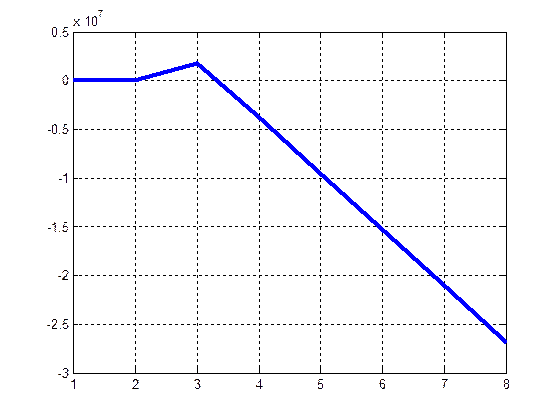
График прибыли в зависимости от числа каналов

n

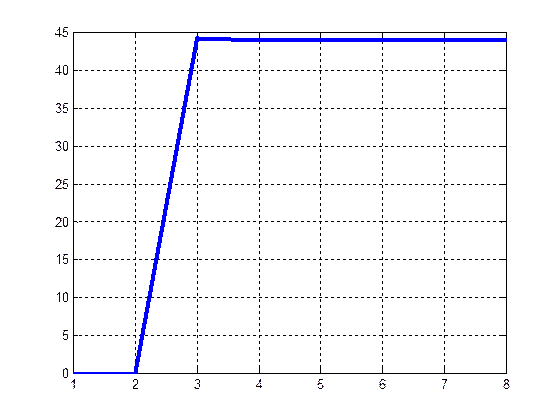
График среднего времени пребывания заявки в системе