Краткие сведения из теории
Матричные испытания являются частным видом физического моделирования. Разработка метода граничных испытаний показала ограниченность их применения, так как каждый параметр какого-либо элемента или РЭА связан сложной функциональной их зависимостью с остальными параметрами элемента или схемы, а также зависит от влияния различных воздействий.
Метод матричных испытаний, являющиеся дальнейшим развитием граничных испытаний, заключается в том, что испытании осуществляют моделирование рабочей области радиоустройства при всех возможных значениях первичных параметров, находящихся в пределах допусков. Для моделирования параметров схем, лежащих в границах, предусмотренных техническим заданием, составляют матрицу состояний. (Матрицей называют систему mn чисел, расположенных в прямоугольную таблицу из m строк и n столбцов). В общем случае работоспособность и надежность ЭМС зависит от большого числа параметров элементов схемы и внешних факторов, воздействующих на величину этих параметров. Для удобства рассмотрим матричные испытания устройства, работоспособность которого зависит только от двух параметров Х1 и Х2, и имеется необходимая информация о характере случайных воздействий, о сигнале и некоторых других закономерностях. Условимся все параметры считать, от которых зависит работа ЭМС, называть определяющими и считать, что диапазон их возможных значений ограничен интервалами:
 и т.д.
и т.д.
Эти интервалы определяются допусками в соответствии с техническими требованиями, предъявляемыми к ЭМС и ее элементам.
Разобьем эти интервалы на одинаковые участки (кванты), число которых соответственно будет m1 и m2. Значение параметров, соответствующие серединам участков, будем называть представителями квантов. Состояние ЭМС, при котором определяющие параметры находятся в заданном кванте и принимают значения представителя кванта, называют ситуацией состояния системы. При двух параметрах, определяющих работоспособность системы, число возможных ситуаций для ЭМС, равно:
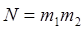 (2.1)
(2.1)
Для общего случая, когда число определяющих параметров равно n (n – мерный случай), число возможных ситуаций равно:
 (2.2)
(2.2)
Каждая ситуация состояния соответствует определенным значениям параметров элементов.
Для того, чтобы учесть одновременное изменение всех определяющих параметров, пользуются последовательностью ситуаций a1, a2, … ai1, …am . Для моделирования возможных ситуаций составляется матрица ситуаций:
 , (2.3)
, (2.3)
где первый индекс при a характеризует параметр, а второй показывает, какому кванту данного параметра он принадлежит.
Наличие матрицы комбинаций случайных величин, характеризующих входные параметры ЭМС, позволяет численным методом определить возможные реализации случайных значений входных параметров. Перебор всех возможных ситуаций для данного устройства осуществляется при проведении матричных испытаний. Очевидно, что некоторые ситуации будут отказовыми, последовательность которых обозначим:
w1, w2, …, wm, … wr.
Зная вероятности появления отказовых ситуаций P1 (t), P2 (t), …Pm (t), …Pr (t) можно определить область работоспособности исследуемого устройства S(X1; X2) (рис. 2.1).
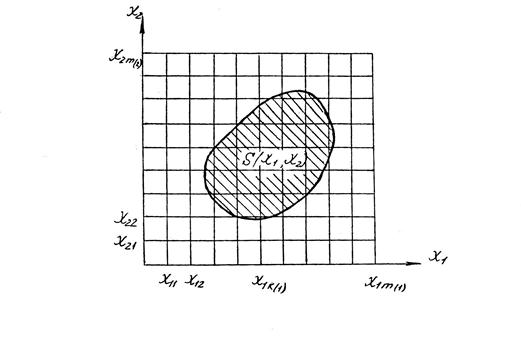
Рис. 2.1. Область работоспособности исследуемого устройства