Математические методы обработки результатов измерений
Для математической обработки результатов многократных измерений и систематических погрешностей необходимо знание основ теории вероятностей и математической статистики.
Случайной величинойназывается величина, изменяющаяся случайным образом, например, случайная погрешность. Случайные величины бывают непрерывными и дискретными.
Дискретная случайная величина может принимать конечное или счетное множество значений. Примером дискретной случайной величины является погрешность многократных измерений. Если множество значений конечно, то вероятность каждого отдельного значения А определяется по формуле
Р (А) = РА = NA / N, где
N – общее количество испытаний,
NA – количество испытаний со значением А.
Непрерывная случайная величина может принимать любое значение из некоторого интервала, конечного или бесконечного. Вероятность попадания в интервал задается как интеграл от функции плотности вероятностей: Р(А<X<B) = 
.
Следует различать понятия "погрешность средства измерения", "погрешность результата измерения" и "погрешность результата многократных измерений". Погрешность результата однократного измерения складывается из погрешностей средства и метода измерений. С помощью вероятностных методов оценивают ожидаемую, т.е. наиболее вероятную, погрешность результата многократных измерений и возможное отклонение результата от ожидаемого значения. Результат измерений можно записать в виде
X = Q + Δ = Q + Θ + δ, где
Х – результат измерения,
Q – истинное значение измеряемой величины,
Δ – абсолютная погрешность результата измерений,
Θ – систематическая составляющая погрешности результата измерений,
δ – случайная составляющая погрешности результата измерений.
После устранения систематической погрешности получаем исправленное значение результата измерений, содержащее только случайную погрешность:
X0 = Q + δ
Оценка случайных погрешностей производится на основании методов теории вероятностей и математической статистики, в основе которых лежат следующие два положения:
1) при большом числе измерений случайные погрешности одинаковой величины, но разного знака, встречаются одинаково часто;
2) большие по абсолютной величине погрешности встречаются реже, чем малые, т.е. вероятность появления погрешности уменьшается с ростом величины погрешности.
Допустим, что было проведено N прямых измерений некоторой физической величины и получены результаты, свободные от систематических погрешностей:
Х1 = Q + ΔX1
Х2 = Q + ΔX2 …
ХN= Q + ΔXN
Суммируя почленно правые и левые части этих равенств, получаем
Разрешая это уравнение относительно истинного значения измеряемой величины, получаем:
Если число измерений достаточно велико (N → ∞), то согласно положениям теории вероятностей, во второй сумме положительные и отрицательные слагаемые взаимно уничтожают друг друга, и сама сумма стремится к нулю. Таким образом, среднее арифметическое результатов измерений выступает в качестве оценки истинного значения измеряемой величины. При ограниченном числе измерений эта оценка имеет погрешность.
Назовем вероятностью попадания величины Х в интервал A<X<B значение P{A<X<B} = 
при N → ∞, где n – число измерений с благоприятным исходом, N – общее число измерений.
Интегральная функция распределения вероятностей – это функция вида
F(A) = P{–∞ < X < A},
т.е. вероятность того, что результат измерений Х окажется меньше заданной величины А. Интегральная функция имеет вид, представленный на рис. 1.2.
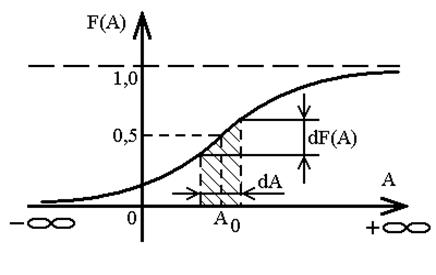
Рис. 1.2. Интегральная функция распределения вероятностей
Свойства интегральной функции распределения вероятностей:
1. 0 < F(A) < 1 
А;
2. F(–∞) = 0, F(+∞) = 1;
3. функция F(A) является неубывающей на всей числовой оси;
4. вероятность события P{A<X<B} = F(B) – F(A).
Особое место занимает точка Х = А0, в которой F(A0) = 0,5, т.е. значения Х с равной вероятностью могут оказаться как меньше, так и больше А0. Наиболее вероятным значением измеряемой величины является такое ее значение 
, при котором первая производная интегральной функции распределения вероятности 
имеет максимум. В точках –∞ и +∞ производная стремится к нулю. Касательная к графику функции F(A) в точке образует наибольший угол с осью абсцисс. Как правило, точки А0 и совпадают и обозначаются символом mA (математическое ожидание значения А)
Дифференциальной функцией распределения вероятностей (или функцией плотности распределения вероятностей) называется функция вида
р(А) = 
, где A1 = A – 0,5 dA, A2 = A + 0,5 dA.
Дифференциальная функция является производной интегральной функции распределения вероятностей. График дифференциальной функции представлен на рис. 1.3.
Рис. 1.3. Дифференциальная функция распределения вероятностей для нормального распределения случайной величины
Свойства дифференциальной функции распределения вероятностей:
1) р(А) ≥ 0 – вероятность любого события не может быть отрицательной;
2) р(–∞) = р(+∞) = 0;
3) 
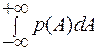= 1 – площадь, ограниченная кривой графика функции плотности вероятностей и осью абсцисс, равна 1, т.е. вероятность полной группы событий равна 1.
Характерное распределение – вид графика функции плотности вероятностей.
Дифференциальные функции распределения вероятностей могут иметь различный вид и описываться различными формулами. Приведем несколько примеров математических моделей законов распределения.
1. Нормальный закон распределения (распределение Гаусса)
р(А) = 
,
где mA и σ – соответственно математическое ожидание и среднеквадртическое отклонение значений случайной (измеряемой) величины, е ≈ 2,71828… – основание натурального логарифма. Вид графика функции плотности вероятностей представлен на рис. 1.3. Значение mA характеризует положение пика максимума распределения, значение σ – крутизну этого пика (чем больше значение σ, тем шире и ниже пик).
2. Распределение Коши
р(А) = 
,
где параметр mA является матожиданием случайной величины, а параметр С играет ту же роль, что и параметр σ в нормальном распределении. Вид графика функции плотности распределения вероятностей подобен представленному на рис. 1.3, с несколько более пологим пиком максимума.
3. Распределение Лапласа (двухстороннее экспоненциальное
р(А) = 
,
где параметры mA и σ – соответственно матожидание и среднеквадртическое отклонение значений случайной величины, е – основание натурального логарифма. Вид графика функции плотности вероятностей представлен на рис. 1.4а. Как видим, распределение Лапласа характеризуется острым, неаналитическим пиком максимума. Но площадь под кривой графика по прежнему равна 1.
4. Равномерный закон распределения
р(А) = 
, при А1 < A < A2;
р(А) = 0, при А < А1 или А > А2
При равномерном распределении равновероятными являются значения из некоторого интервала (А1, А2), появление значения вне этого интервала является невозможным событием. Вид графика функции плотности вероятностей представлен на рис. 1.4б. Площадь под кривой графика равна 1.
а) б)
Рис. 1.4. Виды графиков различных функций
распределения плотности вероятностей:
а) распределение Лапласа; б) равномерное распределение
Случайные погрешности результатов измерения в большинстве случаев подчиняются закону нормального распределения. Широкое распространение нормального распределения погрешностей в измерительной практике (и преобладание нормального распределения в вычислительной практике в целом) объясняется центральной предельной теоремой теории вероятностей.
Центральная предельная теорема теории вероятностей гласит, что если случайная величина зависит от большого количества влияющих на нее величин (факторов), причем влияние каждого конкретного фактора мало по сравнению с суммарным влиянием, и если значение величины определяется по результатам большого числа испытаний, то результаты испытаний распределятся по нормальному закону.
Координата центра распределения определяет наиболее вероятное положение величины на числовой оси. В теории вероятностей существуют три принципиально различных способа определения центра распределения.
1. Определение центра из принципа симметрии. Центром распределения считается такая точка на числовой оси, справа и слева от которой вероятности появления различных значений случайной величины А равны между собой. Это точка А0 в которой значений интегральной функции распределения вероятностей F(А0) = 0,5. Линия F(А) = 0,5 называется медианой вероятности, т.к. она делит график интегральной функции на две равновероятные части. Проекция точки пересечения интегральной функции F(А) с медианой вероятности на числовую ось дает положение центра распределения из условий симметрии (рис. 1.2).
2. Определение центра распределения, как центра тяжести, т.е. такой точки на числовой оси, относительно которой опрокидывающий момент равен нулю.
Рассмотрим график дифференциальной функции распределения вероятностей, на котором выделим элементарный участок площади, называемый элементом вероятности (рис. 1.5).
Рис. 1.5. Нахождение центра распределения как центра тяжести
Из графика видно, что элемент вероятности представляет собой произведение p(A) ´ dA. Опрокидывающий момент такого элемента относительно точки А0 можно представить как dM = r ´ p(A) ´ dA, где r – плечо элемента. Просуммировав моменты всех элементов вероятностей относительно точки А0, получим выражение для опрокидывающего момента всей фигуры
М =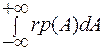 
С учетом того, что нам требуется найти точку, опрокидывающий момент относительно которой равен нулю, получаем уравнение
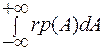= 0
На рис. 1.5 видно, что плечо элемента r = А0 – А. Подставив это выражение в уравнение момента, получаем
Следовательно,
Так как, согласно свойствам дифференциальной функции распределения вероятностей, площадь под кривой графика распределения вероятностей равна единице, т.е.
,
то аналитическое выражение для определения центра распределения окончательно имеет вид
Центр распределения, найденный таким образом, носит название математического ожидания.
Все вышеизложенное справедливо для случая, случайная величина является непрерывно распределенной. В действительности при выполнении практических измерений чаще всего приходится иметь дело с дискретными случайными величинами. Тогда элемент вероятности можно записать как dP = p(A) dA = ΔPi = p(Ai) ΔAi = Pi – вероятность значения Аi (рис. 1.6). При расчете математического ожидания интегрирование сводится к суммированию:
Если все значения равновероятны площади всех прямоугольников на рис. 1.6 равны), последняя формула приобретает вид
Таким образом, оценкой матожидания для дискретных случайных величин является средневзвешенное или среднеарифметическое значение ряда чисел.
Рис. 1.6. Распределение плотности вероятности
для дискретной случайной величины.
3. Центр распределения можно определить как точку, в которой функция плотности распределения вероятностей имеет максимальное значение. При этом координатой центра распределения служит мода распределения. Абсцисса моды распределения находится как точка, в которой первая производная функции плотности вероятностей принимает нулевое значение, то есть
Есть распределения, у которых не существует моды. Например, у равномерного распределения. В этом случае определение центра как моды распределения лишено смысла. Поэтому в теории вероятностей принято оперировать понятием центра распределения, которое правомерно для всех распределений. Это понятие имеет общий характер и не зависит от конкретного способа определения координаты центра.