АЛГОРИТМ ХУКА – ДЖИВСА

ПРЯМЫЕ МЕТОДЫ БЕЗУСЛОВНОЙ МИНИМИЗАЦИИ

 

Этот алгоритм содержит две основные процедуры:

а) исследующий покоординатный поиск в окрестности данной точки, предназначенный для определения направления убывания f (х);

б) перемещение в направлении убывания.

Опишем алгоритм исследующего покоординатного поиска из заданной точки х с приращениями по каждой координате D_j , j = 1, …, n

Шаг 1. Положить 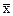= x , i = 1.

Шаг 2. Сделать пробный шаг y= – D_je ^j, где e ^j –j–й базисный вектор. Если f ( ) £ f (y), то перейти к шагу 3, иначе – к шагу 4.

Шаг 3. Сделать пробный шаг y= +D_je ^j . Если f ( ) £ f (y), то перейти к шагу 5, иначе – к шагу 4.

Шаг 4. Положить = у.

Шаг 5. Положить j = j + 1. Если j £ n, то перейти к шагу 2. В противном случае исследующий поиск окончен – получена точка для которой f ( ) < f (y), если ¹ х.

Замечание. В результате исследующего поиска может оказаться, что =х. Тогда исследующий поиск считается неудачным. Если при этом норма приращения D =(D₁,.., D_n ) мала, т.е. ||D|| £ e, где e – заданная точность, то полагают х^* = х. Если заданная точность не достигнута, то полагают D=D/g (постоянная g >1 – коэффициент уменьшения шага) и повторяют исследующий поиск.

Приведем теперь полный алгоритм Хука – Дживса.

Шаг 0. Выбрать начальную точку х⁰ , вектор приращений D =(D₁,.., D_n ), коэффициент уменьшения шага g >1, параметр окончания поиска e > 0.

Шаг 1. Провести исследующий покоординатный поиск из точки х⁰, т.е. найти точку . Если ¹ х , то перейти к шагу 3, иначе – к шагу 2.

Шаг 2. Проверка на окончание поиска. Если ||D||<e, то прекратить поиск и положить х^*=х⁰. Иначе – положить D=D/g и перейти к шагу 1.

Шаг 3. Перемещение из точки х в направлении убывания – х⁰ : положить х¹ = + ( – х⁰) = 2 – х⁰ .

Шаг 4. Провести исследующий поиск в точке х¹ , т.е. найти точку . Если f ( ) < f ( ), то положить х⁰ = , = и перейти к шагу 3. Иначе – положить х⁰ = и перейти к шагу 1.

Пример 3.7. Рассмотрим графическую иллюстрацию решения задачи f (х)=(x₁+ 1)²+х²₂ ®min методом Хука – Дживса из начальной точки х⁰ =(2,3),вектор перемещений D=(1/2,1).

Целевая функция f (х) представляет собой квадрат расстояния между точками х и х^* =(–1,0). Линии уровня f (х) – это окружности с центром в точ­ке х^*. Поэтому значения f (х) в промежуточных точках алгоритма легко сравни­вать, оценивая их расстояния от точки х^* на рис. 3.9. На рисунке пунктиром выделены траектории исследующего поиска, сплошными линиями – перемещения в направлении убывания. Убеди­тесь в соответствии графической иллю­страции описанному алгоритму.

Все описанные выше прямые методы безусловной минимизации функции многих переменных содер­жат детерминированные процедуры поиска точек с меньшим значением функции.

Однако разработано довольно много методов минимизации, где в процедуру поиска точек минимума намеренно вводят эле­менты случайности.

 

Рис. 3.9. К примеру 3.7.