курс ЭСЭУ

Вопросы к зачету по дифференциальным уравнениям

1. 3адачи, приводящие к понятию дифференциальный уравнений. Основные понятия: обыкновенные дифференциальные уравнения, что является его решением, порядок уравнения, интегральная кривая.

 

2. Дифференциальные уравнения первого порядка. Основные понятия: общее и частное решение. Геометрический смысл.

 

3. Задача Коши, теорема о существовании и единственности решения задачи Коши, геометрический смысл теоремы.

 

4. Дифференциальные уравнения с разделяющимися переменными и их решение.

· Решить уравнение ;

· Решить уравнение у' = , удовлетворяющее условию у(4) = 1

· Найти общее решение ДУ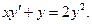

· Решить задачу Коши: у' = 3х , если при х = 1 у = -1

4. Однородные дифференциальные уравнения и их решение.

· Найти общий интеграл уравнения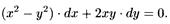

· Найти общий интеграл уравнения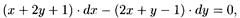

· Решить уравнение

 

5. Линейные дифференциальные уравнения и их решение методом Бернулли.

Проинтегрировать уравнение: а) у' + 2х·у = 2х; б) ху' - 4·у = х2√у;

в) у' + tgх·у = ;г) у' =

 

6. Уравнение Я. Бернулли. Решить уравнение: у'+2ху = 2ху3.

 

7. Дифференциальные уравнения в полных дифференциалах. В каких случаях необходим интегрирующий множитель и как его найти.

  • Решить уравнение
  • Решить уравнение (х2 – у) ·dх + (х2у2 + х) ·dу= 0.
  • найти интегрирующий множитель: а) 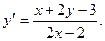б)

8. Уравнения Лагранжа и Клеро.

  • Решить уравнение Клеро а) у = ху' + у'2, б) у = ху′ + у′ — (у′)2, в) у = ху′ — 3(у′)3.
  • Решить уравнение Лагранжа:у = х(1 + у′) + (у′)2.