Доказательство.

Чтобы не усложнять изложение, ограничимся тем случаем, когда множество D ограничено, и, следовательно, является выпуклым многогранником.

Для доказательства воспользуемся следующим известным свойством ограниченных выпуклых множеств:

Если D — замкнутое ограниченное выпуклое множество, имеющее конечное число угловых точек, то любая точка х D может быть представлена в виде выпуклой комбинации угловых точек D*.

* Строгое доказательство данного утверждения см., например, в [14].

Пусть х¹, х²,…,х^m — угловые точки множества D, а х* — точка, в которой целевая функция f достигает максимума.

На основе сформулированного выше утверждения точку х* можно представить в виде выпуклой комбинации угловых точек х¹, х²,..., x^m

Так как х* — точка максимума, то для любого х D сх* ≥ сх. Функция f(x) — линейная, поэтому

cледовательно,

где x^r — угловая точка, удовлетворяющая условию

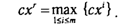
Из (1.10) видно, что сх* ≤ сх^r. В то же время справедливо обратное неравенство: сх* ≥ сх^r. Откуда следует, что сх* = сх^r, т. е. существует по крайней мере одна угловая точка х^r, в которой целевая функция принимает максимальное значение. A

 

Билет 24

Двумерные задачи линейного программирования решаются графически. Для случая N=3 можно рассмотреть трехмерное пространство и целевая функция будет достигать своё оптимальное значение в одной из вершин многогранника.

В общем виде, когда в задаче участвуют N-неизвестных, можно сказать, что область допустимых решений, задаваемая системой ограничивающих условий, представляется выпуклым многогранником в n-мерном пространстве и оптимальное значение целевой функции достигается в одной или нескольких вершинах. Решить данные задачи графически, когда количество переменных более 3 весьма затруднительно. Существует универсальный способ решения задач линейного программирования, называемый симплекс-методом.

Билет 25