Экспоненциальная и логистическая кривые роста численности популяции, их характеристика. 4.04. Экспоненциальный и логистический рост численности популяции
«В 1536 г. испанский аделантадо Педро де Мендоза, закладывая город Буэнос-Айрес, привез в аргентинские пампы 20 коров и 72 лошади. Спустя три года поселение было сожжено дотла индейцами, и испанцы его покинули. Лошади и коровы оказались предоставлены сами себе. Они размножились в пампах, и к 1700 г. численность популяции коров и популяции лошадей достигли миллиона голов каждая. Испанские мореплаватели XVI и XVII вв. систематически завозили на океанические острова коз, чтобы обеспечить себе пропитание на случай кораблекрушения. Один такой путешественник, Хуан Фернандес, завез пару коз на острова Тихого океана вблизи побережья Чили, — острова, которые затем были названы его именем. В 1704 г., когда Александр Селкирк (послуживший Даниэлю Дефо прототипом Робинзона Крузо) был оставлен на этих островах капитаном его корабля, численность стада коз, которым дала начало эта пара, превышала 10 000, и стадо существует до сих пор» (О. Солбриг, Д. Солбриг, 1982).
Вероятно, впервые проблема описания популяционного роста поставлена в «Трактате о счете» («Liber abaci») итальянского ученого Леонардо Фибоначчи, датированной 1202 годом. В книге приводится собрание арифметических и алгебраических задач. Одна из них рассматривает динамику размножения кроликов: «Некто выращивает кроликов в пространстве, со всех сторон обнесенной высокой стеной. Сколько пар кроликов рождается в один год от одной пары, если через месяц пара кроликов производит на свет другую пару, а рожают кролики начиная со второго месяца после своего рождения». Решением задачи является ряд чисел: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 …
Итак, как было ясно уже Фибоначчи, прирост популяции пропорционален ее численности, и поэтому, если рост популяции не ограничивают никакие внешние факторы, он непрерывно ускоряется. Опишем этот рост математически.
Прирост популяции пропорционален численности особей в ней, то есть ΔN~N, где N —численность популяции, а ΔN — ее изменение за определенный период времени. Если этот период бесконечно мал, можно написать, чтоdN/dt=r×N, где dN/dt — изменение численности популяции (прирост), а r— репродуктивный потенциал, переменная, характеризующая способность популяции увеличивать свою численность. Приведенное уравнение называется экспоненциальной моделью роста численности популяции (рис. 4.4.1).
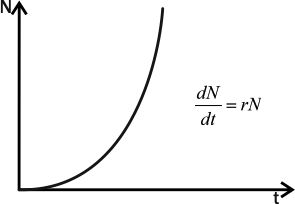
Рис.4.4.1. Экспоненциальный рост
Величину r называют иногда мальтузианским параметром. Английский священник Томас Мальтус был первым, кто обратил внимание на то, что численность населения растет в геометрической прогрессии. Именно знакомство с его работой подтолкнуло и Чарльза Дарвина, и Альфреда Уоллеса к догадке о том, что потомство любых организмов должно «прореживаться» естественным отбором.
Как легко понять, с ростом времени численность популяции растет все быстрее, и достаточно скоро устремляется к бесконечности. Естественно, никакое местообитание не выдержит существования популяции с бесконечной численностью. Тем не менее, существует целый ряд процессов популяционного роста, который в определенном временном промежутке может быть описан с помощью экспоненциальной модели. Речь идет о случаях нелимитированного роста, когда какая-то популяция заселяет среду с избытком свободного ресурса: коровы и лошади заселяют пампу, мучные хрущаки — элеватор с зерном, дрожжи — бутыль виноградного сока и т.д.
Естественно, экспоненциальный рост популяции не может быть вечным. Рано или поздно ресурс исчерпается, и рост популяции затормозится. Каким будет это торможение? Практическая экология знает самые разные варианты: и резкий взлет численности с последующим вымиранием популяции, исчерпавшей свои ресурсы, и постепенное торможение прироста по мере приближения к определенному уровню. Проще всего описать медленное торможение. Простейшая описывающая такую динамику модель называется логистической и предложена (для описания роста численности популяции человека) французским математиком Ферхюльстом еще в 1845 году. В 1925 году аналогичная закономерность была заново открыта американским экологом Р. Перлем, который предположил, что она носит всеобщий характер.
В логистической модели вводится переменнаяK — емкость среды, равновесная численность популяции, при которой она потребляет все имеющиеся ресурсы. Прирост в логистической модели описывается уравнением dN/dt=r×N×(K-N)/K (рис. 4.4.2).

Рис. 4.4.2. Логистический рост
Пока Nневелико, на прирост популяции основное влияние оказывает сомножитель r×Nи рост популяции ускоряется. Когда становится достаточно высоким, на численность популяции начинает оказывать основное влияние сомножитель (K-N)/Kи рост популяции начинает замедляться. Когда N=K, (K-N)/K=0и рост численности популяции прекращается.
При всей своей простоте логистическое уравнение удовлетворительно описывает много наблюдаемых в природе случаев и до сих пор с успехом используется в математической экологии.