Исходные данные для задачи Коши
План выполнения курсовой работы
1. Построить многочлены Лагранжа первой, второй и третьей степени «вручную», для проверки правильности построения выполнить построение многочленов Лагранжа в системе MATLAB. Для выполнения п.5 курсовой работы необходимо построить многочлен Лагранжа четвертой степени. Оценить погрешность интерполирования («вручную» и в системе MATLAB). Построить графики многочленов Лагранжа.
2. Построить алгебраические многочлены наилучшего среднеквадратичного приближения первой степени g1(x) = A1*x+B1 и второй степени g2(x) = A2*x^2+B2*x+C2 «вручную», вычислить величину среднеквадратичного уклонения для g1(x) и g2(x) и построить графики многочленов.
В системе MATLAB проверить правильность построения многочленов «вручную», средствами MATLAB выполнить построение алгебраических многочленов наилучшего среднеквадратичного приближения первой степени g1(x) = A1*x+B1, второй степени g2(x) = A2*x^2+B2*x+C2 и третьей степени g3(x) = A3*x^3+B3*x^2+C3*x+D3.
3. Найти корни многочлена Лагранжа четвертой степени (или его производных в случае, если многочлен Лагранжа четвертой степени не имеет корней) методом бисекции, методом простой итерации и методом Ньютона. Провести сравнительный анализ результатов.
4. Найти один из экстремумов (по выбору) алгебраического многочлена наилучшего среднеквадратичного приближения третьей степени (или его производной в случае отсутствия экстремумов у алгебраического многочлена наилучшего среднеквадратичного приближения третьей степени) различными методами. Провести сравнительный анализ результатов.
5. Решить задачу Коши, в которой функция 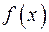 найдена двумя различными методами, как многочлен Лагранжа четвертой степени, и как алгебраический многочлен наилучшего среднеквадратичного приближения третьей степени. Решение задачи Коши предварительно выполнить «вручную» для одной из аналитически восстановленной функции
найдена двумя различными методами, как многочлен Лагранжа четвертой степени, и как алгебраический многочлен наилучшего среднеквадратичного приближения третьей степени. Решение задачи Коши предварительно выполнить «вручную» для одной из аналитически восстановленной функции 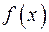 (по выбору) методом Эйлера для крупной сетки, проверить правильность решения в системе MATLAB и получить ломаную Эйлера для более мелкой сетки. С помощью встроенных функций системы MATLAB численно решить задачу Коши для
(по выбору) методом Эйлера для крупной сетки, проверить правильность решения в системе MATLAB и получить ломаную Эйлера для более мелкой сетки. С помощью встроенных функций системы MATLAB численно решить задачу Коши для 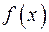 , полученной различными методами приближений функции. Для графического сравнения построить на одном рисунке ломаные Эйлера и графики кривых решения задачи Коши, полученные с помощью встроенных функций ode23 и ode45.
, полученной различными методами приближений функции. Для графического сравнения построить на одном рисунке ломаные Эйлера и графики кривых решения задачи Коши, полученные с помощью встроенных функций ode23 и ode45.
Приложение 1.
Исходные данные для задачи Коши
| № варианта | Функция 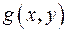
| Начальное условие 
|
| 1. | 
| 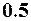
|
| 2. | 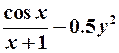
| 
|
| 3. | 
| 
|
| 4. | 
| 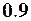
|
| 5. | 
| 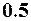
|
| 6. | 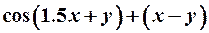
| 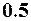
|
| 7. | 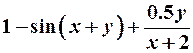
| 
|
| 8. | 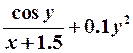
| 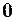
|
| 9. | 
| 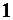
|
| 10. | 
| 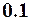
|
| 11. | 
| 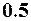
|
| 12. | 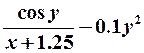
| 
|
| 13. | 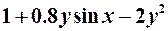
| 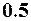
|
| 14. | 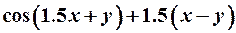
| 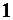
|
| 15. | 
| 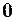
|
| 16. | 
| 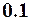
|
| 17. | 
| 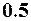
|
| 18. | 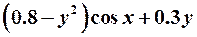
| 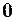
|
| 19. | 
| 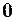
|
| 20. | 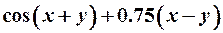
| 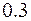
|
| 21. | 
| 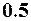
|
| 22. | 
| 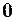
|
| 23. | 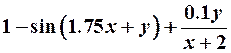
| 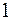
|
| 24. | 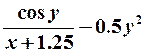
| 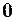
|
| 25. | 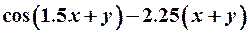
| 
|
| 26. | 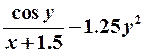
| 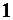
|
| 27. | 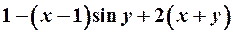
| 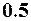
|
| 28. | 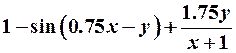
| 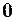
|
| 29. | 
| 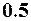
|
| 30. | 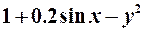
| 
|
Приложение 2.