функциональных рядов

Поточечная (простая )сходимость функциональных последовательностей и

функциональных рядов

 

Пусть все функции f_n(x), n ÎN , определены на множестве X Ì Rи пусть x_o ÎR.

f_n : D _n ® R , , .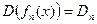

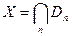Определение. Если числовая последовательность 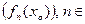N , сходится, то говорят, что последовательность функций 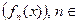N , сходится в точке x_o Î X .

Определение. Последовательность функций 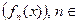N ,сходится на множестве

E Ì X , если 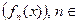N , сходится в каждой точке этого множества.

 

Такую сходимость на множестве Е называют п о т о ч е ч н о й.

 

Множество E Ì X точек, в которых последовательность 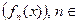N , сходится называют множеством сходимости последовательности 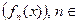N .

 

Пусть на множестве Eсходимости последовательности 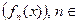N , определена функция f : E ® R , значение которой в любой точке x Î E равно пределу последовательности 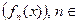N .

Функцию f (x) называют предельной функцией последовательности 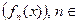N,

или пределом последовательности функций 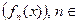Nи пишут

 

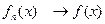при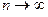

или

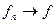при .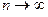

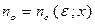По определению предела для любого найдётся номер такой, что при всех 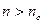выполняется неравенство

,

которое можно записать в виде

.

 

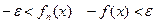Пример 1.Функциональная последовательность 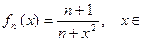R .

Пример 2.Функциональная последовательность .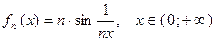

Пример 3.Функциональная последовательность

 

Пусть 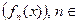N -функциональная последовательность, определённая на множестве

X Ì R.

f_n : D _n ® R , , .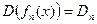

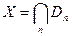Определение. Формальная б е с к о н е ч н а я сумма вида

f₁ (x) + f₂ (x) + …+ f_n (x) + …

называется функциональным рядом, определённым на множестве X Ì Rи

обозначается 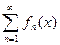или просто .

 

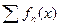Фиксируя какое-либо значение x_o Î X получаем обычный числовой ряд .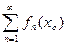

Определение. Если при фиксированном x_o Î X числовой ряд

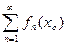
сходится, то говорят, что функциональный ряд

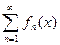
сходится в точке x_o Î X .

Определение. Функциональный ряд 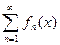сходится на множестве

E Ì X , если он сходится в каждой точке этого множества.

 

Такую сходимость на множестве Е называют п о т о ч е ч н о й.

 

Множество E Ì X точек, в которых функциональный ряд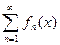

сходится , называют множеством сходимости функционального ряда .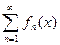

 

Область сходимости может иметь довольно сложную структуру.

 

В конкретных ситуациях область сходимости может совпадать с областью определения,

 

область сходимости может быть частью области определения, а может вообще быть

 

пустым множеством.

 

Пусть на множестве Eсходимости функционального ряда 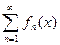определена функция S_n (x) = f₁ (x ) + f₂ (x) + …+ f_n (x),

( ),

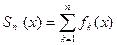которую называют n - ой частичной суммой функционального ряда.

 

Каждый функциональный ряд 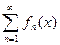является парой двух функциональных

последовательносте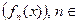й N и 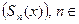N , между которыми устанавливается

взаимно однозначное соответствие: .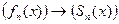

Поэтому каждое свойство функциональных последовательностей перефразируется в некоторое свойство функциональных рядов.

Определение. Функциональный ряд 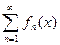сходится на множестве

E Ì X , если он функциональная последовательность 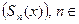Nсходится на множествеE Ì X .

Определение. Если функциональная последовательность 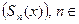Nсходится и

S ( x) - её п р е д е л ь н а я ф у н к ц и я, то S ( x) называютсуммой функционального ряда .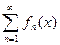

Функция S ( x) определена на множестве E - области сходимости функционального ряда .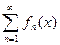

Важно знать какими свойствамиобладает функция S ( x).

Главные среди этих свойств : непрерывность, дифференцируемость и интегрируемость.

Пример 4.Функциональный ряд 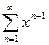, X = (-1; 1).

 

Остаток сходящегося функционального ряда r_n ( x), 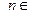N , представляет собой некоторую функцию 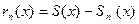. 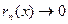при 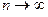в любой точке x Î E.

Многие свойства суммы S ( x) связаны с поведением остатка r_n ( x).

 

§ 2. Равномерная сходимость функциональных последовательностей и функциональных рядов.

 

§ 3. Критерии равномерной сходимости функциональных последовательностей и

функциональных рядов.

3.1. Критерий равномерной сходимости функциональных последовательностей и

функциональных рядов.

3.2. Критерий Коши равномерной сходимости функциональных последовательностей и

функциональных рядов.