Варіант 10.

1. У тетраедрі ABCD дано ребра АВ = b; АС = с; AD = d. Виразити через ці вектори решту ребер тетраедра, медіану DM грані BCD, вектор АО, де О – центр ваги грані BCD.

 

2. Довести, що бісектриси кутів між прямими х –2у – 2 = 0 і 4х + 3у – 12 = 0 взаємно перпендикулярні.

 

3. Через точку (1, -1) провести пряму так, щоб середина її відрізка між прямими х + 2у – 1 = 0 і х + 2у – 3 = 0 лежала б на прямій х – у – 1 = 0.

 

4. Скласти рівняння площини, що проходить через точки (2, 0, 0); (0, 3, 0);
(0, 0, 6) та визначити відстань точки (3, -1, 5) від цієї площини.

 

5. Через дану точку М(1, 0, 1) провести пряму так, щоб її відрізок між площинами х – 2у + 2z – 1 = 0 і 2х – 4у + 4z – 3 = 0 ділився б у відношенні

1 : 2 точкою перетину з прямою .

 

6. Знайти рівняння кола, що проходить через точку (3, 1) і дотикається до еліпса 3х² + у² = 7 в точці (1, 2).

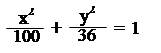7. На еліпсі знайти точку, відстань якої від правого фокуса у

 

чотири рази більша відстані її від лівого фокуса.

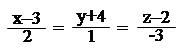8. Знайти рівняння площини, яка проходить через пряму

і па ралельна прямій .

 

9. Визначити вид поверхні та знайти її найпростіше рівняння:

2у² – 8у + 3х – 4z + 12z² – 3 = 0.

 

10. З'ясувати геометричний зміст рівняння та побудувати ескіз:

5у² – 6х + 15 = 0.

Зразки розв’язання задач контрольної роботи №1

1.

1) Довести, що з половини діагоналей будь-якого чотирикутника і будь-якої із його середніх ліній можна скласти трикутник.

Розв’язання.

Нехай АВСD – деякий чотирикутник

М-середина відрізка АВ, N- середина СD.

Тому

Отже, відповідно до умови замкненості, відрізки з довжинами ; 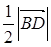і утворюють трикутник.