Варіант 1.
С. Колеснік
Збірник
Контрольних робіт
Аналітична геометрія та лінійна алгебра,
Алгебра та теорія чисел
Методичний посібник
Херсон – 2005
Затверджено на засіданні кафедри алгебри, геометрії та математичного аналізу (протокол № 6 від 9 лютого 2004)
Затверджено на засіданні науково-методичної ради ХДУ (протокол № 3 від 11 лютого 2004 р.)
Рекомендовано вченою радою ХДУ (протокол № 6 від 1 березня 2004 р.)
Автор – Колеснік Світлана Григорівна
доцент кафедри алгебри, геометрії та математичного аналізу
Херсонського державного університету
Рецензенти: Мельник І.І. – кандидат фізико-математичних наук, доцент ХДУ
Таточенко В.І. – кандидат педагогічних наук, доцент ХДУ.
Методичний посібник призначений для студентів фізико-математичних спеціальностей заочної та денної форм навчання, вчителів та учнів ліцеїв, коледжів та шкіл з поглибленим вивченням математики.
Колеснік С.Г.
Збірник контрольних робіт. Аналітична геометрія та лінійна
алгебра, алгебра та теорія чисел: Методичний посібник. Херсон:
Айлант, 2005 р., 112 с.
ISBN 966-630-076-1
ISBN 966-630-076-1 © Колеснік С.Г., 2005
ЗМІСТ
Вступ. 4
Контрольна робота № 1. 6
Зразки розвязання задач контрольної роботи №1. 16
Контрольна робота № 2. 23
Зразки розв’язання задач контрольної роботи №2. 24
Контрольна робота № 3. 32
Зразки розв’язання задач контрольної роботи № 3. 37
Контрольна робота № 4. 54
Зразки розв’язання задач контрольної роботи № 4. 55
Контрольна робота №5. 61
Зразки розв’язання задач контрольної роботи №5. 62
Контрольна робота № 6. 71
Зразки розв’язання задач контрольної роботи № 6. 72
Контрольна робота №7. 78
Зразки розв’язання задач контрольної роботи № 7. 82
Контрольна робота № 8. 86
Зразки роз`язання задач контрольної роботи № 8. 88
Контрольна робота № 9. 92
Зразки розв‘язання задач контрольної роботи № 9. 95
Додаток: таблиці первісних коренів та індексів. 105
ВСТУП
Математичні знання, які студент має придбати в результаті роботи над курсом алгебри, призвані відіграти важливу роль в процесі його подальшого навчання в університеті. Вони будуть потрібні йому для успішного вивчення загальнотеоретичних та спеціальних предметів.
Математичні методи широко використовуються для розв`язання самих різноманітних технічних задач, задач лінійного програмування, задач олімпіадного характеру. Тому студент повинен передбачити, що і після закінчення університету він не раз зіткнеться з необхідністю застосувати свої математичні знання в практичній діяльності.
Курс алгебри призваний також створити у студента міцні навички логічного мислення, так необхідні кожному спеціалісту.
Курс алгебри вивчається на відділенні “ПМСО. Математика” протягом трьох років. Курс аналітичної геометрії та лінійної алгебри на відділенні “Інформатика. ПМСО. Математика” – протягом трьох семестрів, на відділенні “ПМСО. Фізика” – двох семестрів. Курс вищої алгебри на відділенні “Інформатика. ПМСО. МАтематика” вивчається протягом одного семестру.
Робота студента над навчальним матеріалом в основному складається з читання рекомендованих підручників, розв`язання задач, слухання лекцій, складання конспектів, виконання контрольних робіт, складання іспитів.
В процесі вивчення курсу алгебри студент повинен виконати ряд контрольних робіт, які дозволяють як викладачу, так і студенту робити висновок про ступінь засвоєння ним відповідного розділу курса; вказують йому на існуючі недоліки, на бажаний напрямок його подальшої роботи. Допомагають сформулювати питання для консультації з викладачем. Здійснення такої допомоги студенту в його роботі – головна мета цих контрольних робіт.
Контрольні роботи повинні виконуватися самостійно. Несамостійно виконана робота не дає можливості викладачу вказати студенту на недоліки в його роботі, в засвоєнні навчального матеріалу, в результаті чого студент не здобуває необхідних знань.
При виконанні та оформленні контрольної роботи студент повинен додержуватися наступних правил:
а.) у заголовку контрольної роботи повинні бути вписані прізвище студента, його ініціали, назва спеціальності, номер варіанту і дата написання;
б.) контрольну роботу слід виконувати в окремому зошиті з полями для зауважень викладача;
в.) розв`язання контрольних робіт слід розташовувати в порядку номерів, вказаних в завданнях; перед розв`язанням кожної задачі треба виписувати повністю її умову;
г.) розв`язання задач та пояснення до них слід викладати докладно, охайно, без скорочень слів, супроводжувати у випадку необхідності посиланням на теорію, малюнки можна виконувати від руки.
Студенти денної форми навчання спеціальності “ПМСО. Математика” повинні виконати з курсу “Алгебра і теорія чисел” 12 контрольних робіт; заочної форми – 6 робіт.
Студенти спеціальності “Інформатика. ПМСО. Математика” з курсу “Аналітична геометрія та лінійна алгебра” повинні виконати 6 контрольних робіт, з курсу “Вища алгебра” – 2 роботи. Студенти спеціальності “ПМСО. Фізика” – 4 контрольні роботи.
Цей збірник містить 9 контрольних робіт. Матеріал деяких контрольних робіт може бути розбито на дві контрольні роботи. Це стосується контрольних робіт № 1, 2, 3, 9.
Кожна контрольна робота може бути використана як контрольний зріз знань з певної теми.
У зв`язку з тим, що контрольні роботи виконуються і на заочному відділенні. де студенти мають меншу можливість для одержання консультації викладача, для кожної контрольної роботи наводяться зразки розв`язання задач.
Курс “Алгебра і теорія чисел” студенту рекомендується вивчати або за підручником
С. Т. Завало, В. Н. Костарчук. Б. І. Хацет “Алгебра і теорія чисел.” К., “Вища шк.”, 1977,
або
Л. Я. Куликов «Алгебра и теория чисел», М., «Высш. шк.», 1979.
Курс “Аналітична геометрія і лінійна алгебра” –
А. А. Дадаян, в. А. Дударенко «Алгебра и геометрия», М., «Вышэйшая шк.», 1989.
И. Я. Бакельман «Аналитическая геометрия и линейная алгебра», М., «Просвещение», 1976.
И. И. Привалов «Аналитическая геометрия», М., «Госиздат», 1977.
Слід попередити студента, що основні поняття аналітичної геометрії, лінійної алгебри, вищої алгебри, теорії чисел в різних підручниках трактуються по-різному. Тому одночасне користування декількома підручниками, як правило, може викликати деякі труднощі, скласти у нього небезпечну плутанину в уявленнях.
Тому студент повинен з самого початку обрати собі основні підручники та потім додержуватися одного з них.
Контрольна робота № 1
Варіант 1.
1. Довести, що із медіан трикутника можна побудувати новий трикутник (застосовуючи апарат векторної алгебри).
2. Знайти точку симетричну з точкою Q(-2,-9), відносно прямої
2x + 5y – 38 = 0.
3. Скласти рівняння прямої, яка проходить через точку перетину прямих
2x + y – 2 = 0 і x – 5y – 23 = 0 та ділить пополам відрізок АВ,
де А(5,–6), В( –1,4).
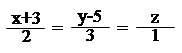 |
4. З усіх прямих, що перетинають дві прямі: і


знайти ту, що паралельна прямій
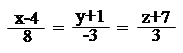 | |||
 | |||
5. Знайти відстань між прямими
6. Через дві точки А(0, 1, -2) і В(2, 1, 0) провести площину перпендикулярну до площини 3x – y + 2z = 0.
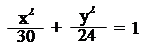 |
7. Знайти ті дотичні до еліпса , які паралельні прямій
2x – y +17 = 0.
8. Написати рівняння гіперболи з фокусами в точках (3, 0); (-3, 0) та ексцентрисите-том e = 2.
9. Визначити тип поверхні та знайти її найпростіше рівняння:
2x2 + 4y2 – z2 + 8x + 8y – 5 = 0.
10. З¢ясувати геометричний зміст рівняння та побудувати ескіз x2 – 2y2 = 4.