Вопросы к лабораторной работе 1

МЕТОДЫ ОПТИМИЗАЦИИ: ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Гомель 2014

Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет

имени Франциска Скорины»

Т. П. Бышик, В. Л., Мережа

МЕТОДЫ ОПТИМИЗАЦИИ: ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Практическое руководство для лабораторных занятий

для студентов специальности

1-31 03 03 Прикладная математика (по направлениям),

1-31 03 06-01 Экономическая кибернетика

Гомель

ГГУ им. Ф. Скорины

УДК

ББК

Рецензенты:

заведующий кафедрой вычислительной математики и программирования учреждения образования «Гомельский государственный университет имени Франциска Скорины», кандидат физико-математических наук, доцент Д.С. Кузьменков;

кандидат технических наук, доцент кафедры прикладной математики УО «БелГУТ» С.И. Жогаль

Рекомендовано к изданию учебно-методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины»

Бышик Т. П.

Методы оптимизации: Линейное программирование. Практ. рук-во / В. Л. Мережа; М–во образования РБ, Гомельский гос. ун-т им. Ф. Скорины. – Гомель: ГГУ им. Ф. Скорины, 2014. – с.

ISBN XXX-XXX-XXX-XXX-X

В настоящем руководстве представлены материалы для практического выполнения лабораторных работ по разделу «Линейное программирование» курса Методы оптимизации. Каждая работа содержит постановку задачи, алгоритмы или схему её решения, снабжена иллюстративными примерами, вариантами индивидуальных заданий и вопросами.

Целью руководства является оказание помощи студентам специальности 1-31 03 03-01 «Прикладная математика (по направлениям и 1-31 03 03-06 Экономическая кибернетика
в выполнении лабораторных работ.

УДК

ББК

ISBN XXX-XXX-XXX-XXX-X

ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Лабораторная работа 1

Метод применим к задачам линейного программирования с двумя переменными:

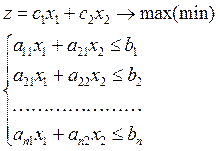
(1) (2)

Алгоритм:

1. В декартовой системе координат на плоскости строим множество Х планов задачи как пересечение k полуплоскостей, задаваемых линейными неравенствами системы (2).

При этом возможен один из случаев:

а) Х – пустое множество;

б) Х – выпуклый многоугольник;

в) Х – выпуклая неограниченная многоугольная область.

Если а), то задача не имеет решения; б) или в) – переходим к п.2.

2. По целевой функции Z строим вектор (градиент целевой функции), через начало координат проводим прямую Z₀ (линию нулевого уровня целевой функции): .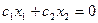

3. При решении задачи максимизации (минимизации) прямую Z₀перемещаем параллельно в направлении вектора 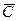(вектора 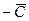) в наиболее отдалённую точку А (точку В) множества планов Х. Координаты точки А (точки В) и составляют оптимальный план задачи максимизации (минимизации) функции Z на множестве Х.

Если множество Х – ограничено, то задача всегда имеет решение. Если же Х – неограниченная многоугольная область, то задача может не иметь решения в случае, когда не существует наиболее удалённой точки, т.е. целевая функция неограниченно возрастает (убывает) на Х.

Если задача имеет оптимальный план, то он достигается либо в одной из вершин границы множества Х, либо на одной из её сторон (альтернативный оптимум).

Замечание. Некоторые задачи линейного программирования с числом переменных n>2 могут быть сведены к эквивалентным линейным задачам с двумя переменными. Для этого систему ограничений-равенств исходной задачи приводим к единичному базису. Определяем из неё базисные переменные (эти выражения называют уравнениями связи). Подставляем их в целевую функцию и ограничения-неравенства задачи. После решения полученной эквивалентной задачи с двумя переменными, решение исходной задачи (базисные переменные) находят из уравнений связи.

Пример. Решить графическим методом задачу:

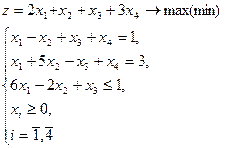(3)

Решение:

1. Приводим систему ограничений-неравенств к единичному базису

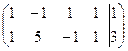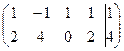à à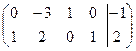

Уравнения связи имеют вид:

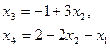(4)

2. Исключаем базисные переменные х₃, х₄из задачи (3):

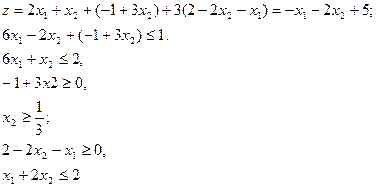
3. Обозначив u=z-5, получаем задачу (5) эквивалентную задаче (3):

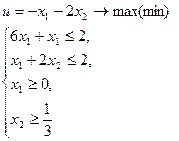(5)

4. На плоскости х₁Ох₂ строим множество Х планов задачи (5), вектор 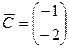, линию нулевого уровня u=0 и линии уровней u=u_max, u=u_min.

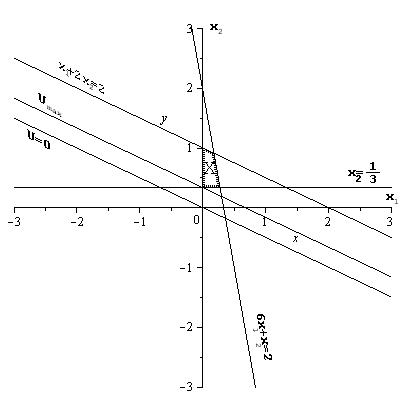
5. Анализ. Область Х – четырёхугольник ABCD. В точке А (0, ) целевая функция u имеет максимальное значение u_max = u (0, ) = - .

Функция u имеет минимальное значение во всех точках отрезка ВС, так как линии уровня функции u параллельны этому отрезку, задача минимизации имеет альтернативный оптимум.

Имеем В (0,1), С ( .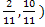

Координаты произвольной точки отрезка ВС можно записать

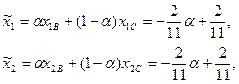
- общее решение задачи минимизации функции u.

Используя решение задачи (5) и уравнения (4), получаем решение исходной задачи (3).

х₁=0, х₂= 1/3, х₃=0, х₄= 4/3 – оптимальный план задачи максимизации.

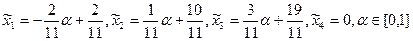- оптимальный план задачи минимизации, Z_max=4, Z_min=3.

Задание. Графическим методом решить следующие задачи:

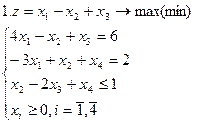
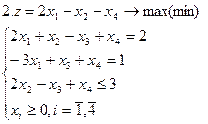
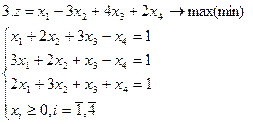
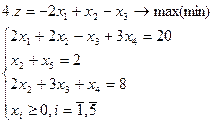
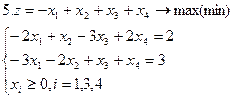
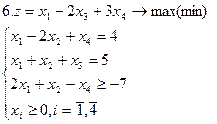
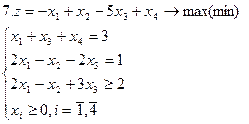
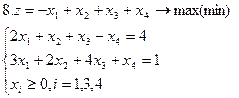
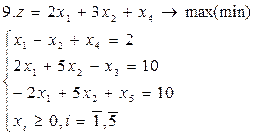
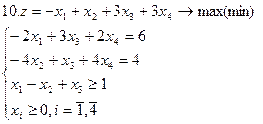
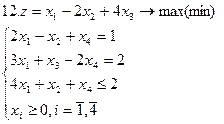
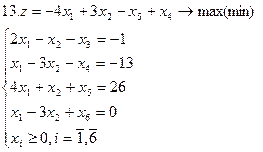
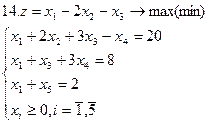
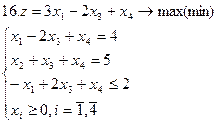
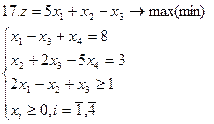
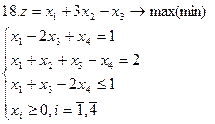
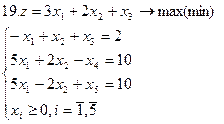
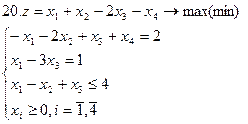
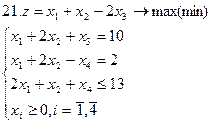
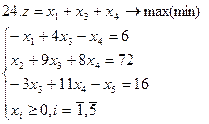
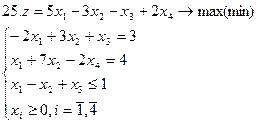
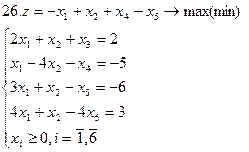
Вопросы к лабораторной работе 1

1. Постановка задачи оптимизации;

2. Определение оптимального плана;

3. Определение локального оптимального плана;

4. Определение минимизирующей последовательности;

5. Постановка производственной задачи.

СИМПЛЕКС- МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Лабораторная работа 2

Симплекс-метод применяется к задачам линейного программирования, которые в канонической форме обладают свойствами: ранг матрицы системы основных ограничений равен числу уравнений, ограничения задачи не противоречивы, причём известен или легко строится начальный базисный план.