Одношаговая оценка методом наименьших квадратов (1-МНК)

ЗАПОРОЖСКИЙ ИНСТИТУТ ЭКОНОМИКИ И

ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Методическое пособие

по дисциплине “Эконометрия”

для студентов дневной и заочной форм обучения

специальностей:

7.050107 «Экономика предприятий»;

7.050104 «Финансы»;

7.050201 «Менеджмент организаций»;

7.050102 «Экономическая кибернетика»;

7.050103 «Международная экономика»;

7.050106 «Учет и аудит»

Запорожье

Методическое пособие по дисциплине “Эконометрия” часть 1 – «Статистические оценки и тесты в экономических моделях», часть 2 – «Анализ динамических рядов и кластерный анализ» для студентов дневной заочной форм обучения специальностей: 7.050107 “Экономика предприятий; 7.050104 “Финансы и кредит”; 7.050102 “Экономическая кибернетика”; 7.050106 “Учет и аудит”; 7.050103 “Международная экономика”; 7.050201 “Менеджмент организаций”. / сост. к.э.н., доц. Двигун А.А., к.ф.-м.н., доц. Гнеушев А.А., к.т.н. –Запорожье.: ЗИЭИТ, 2003 г., - с.

Составители:

к.э.н., доцент Алла Александровна Двигун,

к.ф.-м.н., доцент Александр Николаевич Гнеушев

Обсуждены на заседании

кафедры экономики предприятия и международной экономики

протокол № ____________

от “___” __________ 2003 г.

зав. Кафедрой ________________

к.э.н., доц. А.А. Двигун

Содержание

ВВЕДЕНИЕ

Эконометрия сочетает две области знаний – экономическую теорию и статистику и применяет математические методы к рядам экономических данных. Изучение эконометрии дает обзор эконометрических моделей, важнейших методов оценки параметров и тестирования гипотез. Знания, полученные при ее изучении, позволяют интерпретировать результаты экономических исследований, а также определять формы и типы эконометрических моделей, позволяющие получить наиболее эффективную помощь при принятии решений.

Одношаговая оценка методом наименьших квадратов (1-МНК)

а) Линейная регрессионная модель состоит из двух основных частей:

1. Линейной стохастической функции регрессии;

2. Предпосылок о стохастических и прочих свойствах составных частей этого уравнения.

Для нее характерно то, что ее регрессоры (независимые переменные) не случайные (детерминированные) величины. Однако эта предпосылка не выполняется для многих прикладных моделей, поэтому в группу регрессоров включают стохастические величины и рассматривают обобщенные классические модели. При этом объект исследования представляют регрессионной функцией:

, (1.1)

где Y – регрессанд, X₁, X₂, …, X_К – регрессоры, U – случайные переменные.

Для реализации случайных переменных Y_t и U_t уравнение (1.1) примет вид:

(1.2)

Чтобы статистически оценить параметры регрессионной модели, необходимы ряды данных длиной Т для регрессандов (Y) и для каждого из К регрессоров (переменных Х). При этом длина рядов наблюдений должна быть больше количества регрессоров (T>K). Длина временных рядов образует опорный (базовый) период. Для наблюдаемых в моменты времени t=1, 2, …, T значений можно записать Т уравнений регрессии:

, (1.3)

где

(1.4)

Вектор наблюдений Y и матрица наблюдений Х образуют матрицу данных D.

(1.5)

Она содержит все данные, необходимые для статистической оценки вектора коэффициентов регрессии и прочих параметров модели.

б) Метод оценки регрессионных коэффициентов 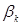, в котором применяется сумма квадратов ошибок как мера качества адаптации эмпирической функции к наблюдаемым данным, называется одношаговым методом наименьших квадратов (1-МНК). Ошибка уравнения для t-го наблюдения равна:

(1.6)

Тогда сумма квадратов ошибок для Т наблюдений имеет вид:

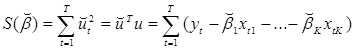(1.7)

или

Дифференцируя по , получим, с учетом необходимого условия существования минимума ( ):

, (1.8)

где 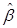- вектор коэффициентов регрессии минимизирующий ; выражение (1.8) называется системой нормальных уравнений. Домножив слева равенство (1.8) на обратную матрицу , получим формулу для вычисления вектора 1-МНК оценок 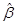для :

(1.9)

Порядок расчетов по формуле (1.9) может быть следующим:

1. Вычислить ;

2. Определить вектор ;

3. Найти матрицу обратную матрице ;

4. Рассчитать 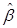как результат произведения на .

Подставив 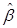в оцениваемое уравнение, получим оцененную с помощью 1-МНК эмпирическую регрессионную функцию:

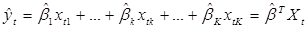(1.10)

Эмпирический коэффициент определяет количество единиц, на которое изменится при изменении X_K на единицу при прочих равных условиях.

Все Т значения – прогноз величины Y (величины ее математического ожидания) образуют вектор :

(1.11)

Тогда 1-МНК оценщик вектора возмущений u имеет вид:

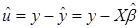(1.12)

Важной характеристикой регрессионной модели является дисперсия возмущений . Ее величина должна быть как можно меньше. 1-МНК оценщик для можно вычислить по одной из формул:

(1.13)

(1.14)

где - сумма квадратов ошибок; 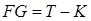- количество степеней свободы; - сумма общих квадратов.

Для t – тестирования гипотез по отдельным коэффициентам регрессии и их линейным комбинациям необходимо знать элементы ковариационной матрицы. Ковариационная матрица для , оцененная методом 1-МНК, может быть представлена следующим образом:

(1.15)

На главной диагонали оцененной ковариационной матрицы , k-ый элемент является 1-МНК оценщиком дисперсии k-го коэффициента , а элемент , расположенный вне диагонали, является 1-МНК оценщиком ковариации между и . Наиболее желательными являются, по возможности, узкие доверительные и прогнозные интервалы. И, как следствие, меньшие оцененные дисперсии и ковариации.

Можно показать, что 1-МНК обеспечивает в классической регрессионной модели многие желательные статистические свойства оценщика (линейность, несмещенность, состоятельность и др.). Поэтому этот метод является оптимальным методом оценки классической регрессионной модели. Однако эта модель мало подходит для реальных экономических и социальных исследований. Следовательно, 1-МНК теряет ряд своих свойств при отклонении условий от лабораторных. Но классическая модель и относящиеся к ней методы оценки и проверки статистических гипотез, образуют основу для развития обобщенных моделей, а также соответствующих методов их оценки и тестирования.