Табулирование функции на конечном отрезке.
Затабулируем значения функции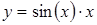 
на отрезке 
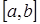в 
в 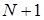точках.
Разобьем отрезок 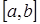на N равных частей точками 
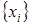, где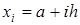 
, при этом 
, 
, 
.
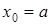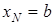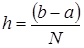Для табулирования значений функции необходимо организовать цикл перебора точек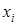 
отрезка 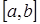, где i изменяется от 0 до N с шагом 1, и в каждой точке надо вычислить и вывести значение функции 
.
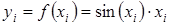Заполним таблицу имен объектов.
| Имя объекта в задаче | Имя объекта в блок-схеме | Тип объекта | Примечания |
| i | I | Целая переменная | счетчик цикла |
| a | A | Вещественная переменная | начало отрезка |
| b | B | Вещественная переменная | конец отрезка |
| N | N | Целая переменная | число отрезков дел. |
| h | H | Вещественная переменная | длина отрезков дел. |
| xi | XI | Вещественная переменная | точки деления |
| yi | YI | Вещественная переменная | значения функции |
Схема алгоритма по шагам запишется следующим образом:
Ш1. Ввод A,B,N.
Ш2. H присвоить (B-A)/N.
Ш3. I присвоить 0.
Ш4. Если I<=N, то перейти на Ш6.
Ш5. Конец.
Ш6. XI присвоить A+H*I.
Ш7. YI присвоить SIN(XI)*XI.
Ш8. Вывод XI,YI.
Ш9. I присвоить I+1.
Ш10.Перейти на Ш4.
Блок-схема этого алгоритма приведена на рис.2.8.
 |
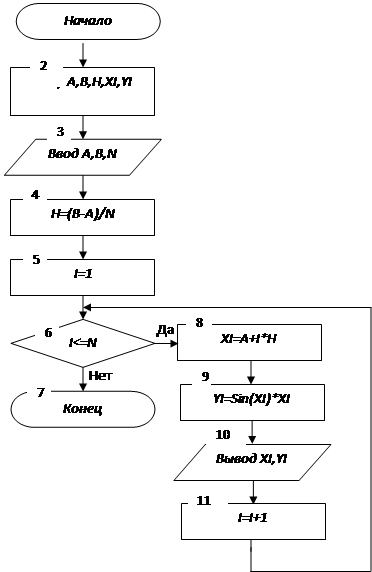Рис.2.8 Блок-схема алгоритма табуляции функции
Поясним работу алгоритма таблицей трассировки для N=3, A=0, B=3.
| № действия | №оператора | |
Ввод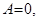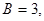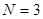   
| ||
| ||
| ||
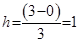
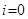
| 0 £ 3, Да | ||
| ||
| ||
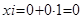
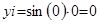
Вывод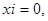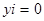  
| ||
| ||
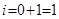
| переход на 4 | ||
| 1 £ 3, да | ||
| ||
| ||
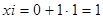
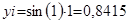
Вывод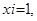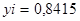  
| ||
| ||
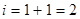
| переход на 4 | ||
| 2 £ 3, да | ||
| ||
| ||
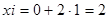
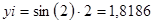
Вывод  ;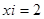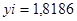 
| ||
| ||
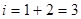
| переход на 4 | ||
| 3 £ 3, да | ||
| ||
| ||
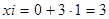
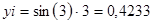
Вывод  ;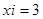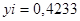 
| ||
| ||
| переход на 4 | ||
| 4 £ 3, нет | ||
| Конец |
В результате программирования должна получиться следующая программа:
PROGRAM TABUL;
VAR I, N: INTEGER;
A,B,H,XI,YI: REAL;
BEGIN
WRITELN('ВВЕДИ ЗНАЧЕНИЕ A,B,N');
READLN(A,B,N);
H:=(B-A)/N;
FOR I:=0 TO N DO
BEGIN
XI:=A+I*H;
YI:=SIN(XI)*XI;
WRITELN('XI=',XI:10:4, ' YI=',YI:10:4);
END;
END.
Для всех заданий этого раздела следует разработать алгоритм и программу.
1. По введенным с клавиатуры значениям X, m вычислить S:
2. По введенным с клавиатуры значениям X и m вычислить P:
3. По введенным с клавиатуры значениям A, B, N, M и X вычислить S:
4. По введенным с клавиатуры значениям A, B, n и X вычислить S:
5. По введенным с клавиатуры значениям A, B, N, M и X вычислить S:
6. Вычислить сумму S значений функции Y = f(x):
.
7. Вычислить сумму S значений функции Y = f(x):
8. По введенным с клавиатуры значениям X вычислить произведение S:
9. Для заданного с клавиатуры значения N найти (2·N)!!
10. Для заданного с клавиатуры значения N найти (2·N+1)!!
11. Найти сумму всех целых чисел, кратных 5, из отрезка [A, B].
12. Найти произведение всех целых чисел, кратных 7, из отрезка [A, B].
13. Найти сумму всех целых чисел, дающих при делении на 5 в остатке 3, из отрезка [A, B].
14. Найти произведение всех целых чисел, дающих при делении на 7 в остатке 4, из отрезка [A, B].
15. Найти сумму квадратов всех целых чисел, дающих при делении на 5 в остатке 2, из отрезка [A, B].
16. Найти сумму кубов всех целых чисел, дающих при делении на 7 в остатке 5, из отрезка [A, B].
17. Найти сумму логарифмов всех целых чисел кратных 6 из отрезка [A, B].
18. Найти сумму логарифмов всех целых чисел, дающих при делении на 3 в остатке 1 из отрезка [A, B].
19. Дан отрезок [A, B]. Вычислить количество чисел этого отрезка, являющихся квадратами целых чисел.
20. Найти наименьшее общее кратное трех заданных с клавиатуры натуральных чисел K, L, M. Если таковых нет, вывести на экран сообщение "NO SOLUTION".
21. Даны натуральные числа M и N. Определить их наименьшее общее кратное.
22. Вычислить сумму всех нечетных чисел от А до В.
23. Дан отрезок [A, B]. Найти сумму всех отрицательных чисел из этого отрезка.
24. Вычислить сумму и произведение 10 членов арифметической прогрессии, где начальный член равен 2, а приращение равно 3.
25. Найти среднее арифметическое квадратов всех целых чисел из отрезка [A, B].
26. Найти сумму кубов всех целых чисел, кратных 8, из отрезка [A,B].
27. Найти среднее арифметическое всех целых чисел из отрезка [A,B].
28. Даны натуральные числа M и N. Определить их наибольший общий делитель.
29. Найти сумму всех целых чисел из отрезка [A,B], которые кратны 5 и 3 одновременно.
30. Найти произведение всех целых чисел из отрезка [A,B], которые кратны 6 и 9 одновременно.