Примеры

1.1. Имеется резистор сопротивлением 5,1 МОм, через который протекает ток, равный 200 мкА. Максимальное значение мощности рассеяния P для резистора P_max = 250 мВт. Рассчитать значение P для данного тока и сравнить с P_max, а также рассчитать с точностью до единиц микроампер максимально возможное значение тока I_max, соответствующее P_max.

Решение:

P = I ²R = 0,204 Вт = 204 мВт < P_max;

I_max = = 221мкА.

 

1.2. Имеется конденсатор емкостью 100 пФ. В начальный момент опыта конденсатор разряжен, затем его в течение 20 мкс заряжают постоянным током, значение которого требуется определить. После этого измеряют напряжение на конденсаторе, которое оказывается равным 1 мВ. Определите выраженное в наноамперах значение тока.

Решение:

I = U C / t = 5 нА.

 

1.3. Верхняя граница рабочей полосы частот электронно-лучевого осциллографа определяется спадом его амплитудно-частотной характеристики (т.е. уменьшением чувствительности канала вертикального отклонения S_y при увеличении частоты входного напряжения относительно значения чувствительности на постоянном токе S_y,0) на 3дБ. Выразите соответствующее изменение чувствительности d_Sy в процентах.

Решение:

3 дБ = 20lg S_y,0 – 20lg S_y = 20lg(S_y,0/ S_y );

d_Sy = (S_y – S_y,0) 100% / S_y,0 = [ (S_y / S_y,0) – 1 ]100 %;

S_y / S_y,0 = 10 ^–0,15 = 0,707946;

d_Sy » –29 %.

 

1.4. Часто при вычислении относительной погрешности d пользуются приближенной формулой, при этом в знаменатель вместо истинного или действительного значения измеряемой величины подставляют измеренное значение. Полученное в результате такого расчета значение относительной погрешности d¢ отличается от d на «погрешность погрешности» d_погр. Выразите d_погр через d.

Решение:

d¢ = D / x = D / (x_и + D) = d / (1 + d);

d_погр = (d¢ – d) / d = –d / (1 + d);

d_погр » –d, так как обычно d << 1.

 

1.5. При измерении величины x возникает систематическая погрешность, относительное значение которой d остается постоянным во всем диапазоне измерений. Полагая, что значение d известно, выведите формулу для расчета скорректированного (свободного от указанной погрешности) значения измеряемой величины x¢.

Решение:

D = x – x¢= d x¢; x¢ = x / (1 + d).

 

1.6. Измеренное значение сопротивления R = 100,0 Ом. Предел допускаемой относительной погрешности измерения d_п = 1,0 %. Найдите интервал, в котором должно находиться R_и — истинное значение сопротивления.

Решение:

D = R – R_и ; R_и = R – D; –D_п £ D £ D_п;

R – D_п £ R_и £ R + D_п;

D_п @ d_п R / 100 % = 1,0 Ом;

99,0 Ом £ R_и £ 101,0 Ом.

 

1.7. Резистор, сопротивление которого требуется измерить, соединен последовательно с мерой сопротивления. Номинальное значение меры — R₀ = 1 кОм. Образовавшаяся цепь подключена к источнику стабильного тока I. Вольтметром, входное сопротивление которого R_V = 100 кОм, поочередно измеряют падения напряжения на обоих резисторах. Полученные значения — соответственно для измеряемого сопротивления и сопротивления меры, U = 3,5 В и U₀ = 0,5 В. Искомое значение вычисляют по формуле R = R₀ U / U₀, в которой не учитывается конечное значение R_V, из-за чего возникает методическая погрешность d_м. Рассчитайте значение d_м.

Решение:

R = 7 кОм;

U = I R_и R_V / (R_и + R_V); U₀ = I R₀ R_V / (R₀ + R_V);

R = R_и (R₀ + R_V) / (R_и + R_V);

R_и = R_V R / (R₀ + R_V – R);

d_м = (R – R_и) 100 % / R_и = (R / R_и – 1) 100 % ;

d_м = (R₀ – R) 100 % / R_V = – 6,0 %.

 

1.8. Выразите абсолютную погрешность взаимодействия для представленной ниже схемы через сопротивления резисторов R₁, R₂, R₃, R₄, показание вольтметра U и его входное сопротивление R_V.

 

 

 

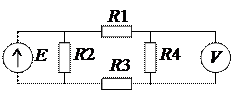
Решение:

D_вз = – U R_экв / R_V. Для определения выходного сопротивления эквивалентного источника напряжения следует заменить источник ЭДС E коротким замыканием и вычислить сопротивление получившейся цепи между точками подключения вольтметра: R_экв = (R₁ + R₃) R₄ / (R₁ + R₃ + R₄).

 

1.9. Выразите абсолютную погрешность взаимодействия для представленной ниже схемы через сопротивления резисторов R₁, R₂, R₃, показание амперметра I и его входное сопротивление R_A.

 

 

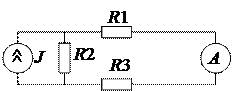Решение:

D_вз = – I R_A / R_экв ; для определения выходного сопротивления эквивалентного источника тока следует заменить источник тока J разрывом и вычислить сопротивление получившейся цепи между точками подключения амперметра: R_экв = R₁ + R₂ + R₃.

 

1.10. Имеется три средства измерений: СИ1, СИ2, СИ3. Обозначения их классов точности, соответственно — 1,0; 0,2 ; 0,1/0,05. Представьте для каждого из этих средств измерений выражения предельных значений основной абсолютной, основной относительной и основной приведенной погрешностей. При этом значение измеряемой величины обозначьте как x, а нормирующее значение как x_N.

 

Решение: СИ1: D_о.п = 0,01 x_N ; d_о.п = (x_N / x) %; g_о.п = 1,0 %;

СИ2: D_о.п = 0,002 x ; d_о.п = 0,2 %; g_о.п = (0,2 x / x_N) %;

СИ3: D_о.п = 0,0005 x + 0,0005 x_N ;

d_о.п = 0,1 % + 0,05 % ^. [½x_N / x½ – 1];

g_о.п = (0,05 x / x_N + 0,05) %.

 

1.11. Какой поддиапазон измерений моста — (0…100) Ом, (0...1000) Ом, (0...10000) Ом, следует выбрать для наиболее точного измерения сопротивления R, значение которого близко к 50 Ом, если предел допускаемой инструментальной составляющей относительной погрешности измерений d_и.п = [1,0 + (2,0 / R)] %, длина шкалы (число делений) a_к = 1000, а показания при отсчете округляются до целого числа делений?

 

Решение: d_п = d_и.п + d_отс.п;

d_и.п = [1,0 + (2,0 / 50)] % @ 1,0 % (для всех поддиапазонов);

d_отс.п @ d_кв.п ; d_кв.п = 50 % ^. q / R; q = R_к / (n a_к); n = 1;

d_отс.п (R_к = 100 Ом) = 0,10 %;

d_отс.п (R_к = 1000 Ом) = 1,0 %;

d_отс.п (R_к = 10000 Ом) = 10 %.

 

1.12. Требуется выбрать один из двух поддиапазонов измерений магнитоэлектрического вольтметра класса точности 1,0 — (0…15)В и (0…30)В, так чтобы минимизировать максимальную, без учета знака, погрешность измерения напряжения, значение которого близко к 10 В. Измерения проводятся при нормальных условиях, погрешность отсчитывания пренебрежимо мала, выходное сопротивление источника напряжения R_и не превышает 20 Ом (вариант 1) или 200 Ом (вариант 2), ток полного отклонения для указанных поддиапазонов измерений I_п.о= 3мА?

 

Решение:

½D½_max = D_о.п + ½D_вз½_max;

D_о.п = 0,01 g_о.п U_к;

½D_вз½_max = U R_{и max} / R_V; R_V = U_к / I_п.о;

1) U_к = 15 В: ½D½_max = 0,19 B;

U_к = 30 В: ½D½_max = 0,32 B;

2) U_к = 15 В: ½D½_max = 0,55 B;

U_к = 30 В: ½D½_max = 0,50 B.

 

1.13. Номинальная функция преобразования цифроаналогового преобразователя (ЦАП) имеет следующий вид: I_ном = 4 мА + 16 мА ( N / N_max), где N — код на входе ЦАП, N_max = 2^m – 1, m = 16 — число двоичных разрядов входного кода ЦАП. Нормирующее значение для входа — N_N = N_max, для выхода — I_N = 20 мА. После подачи на вход ЦАП кода N = 2¹⁴ определено действительное значение выходного тока I_д = 8,002 мА. Рассчитайте D_вх, d_вх, g_вх, D_вых, d_вых, g_вых.

 

Решение:

D_вых = I_д – I_ном = 8,002 мА – [4 мА + 16 мА 2¹⁴ / (2¹⁶ – 1)];

D_вых = 0,00194 мА » 0,0019 мА;

d_вых = D_вых 100 % / I_ном = 0,024 %;

g_вых = D_вых 100 % / I_N = 0,0097 %;

D_вх = N_p – N, где N_p — расчетное значение кода;

N_p = (I_д – 4 мА) N_max / 16 мА = 16392;

D_вх = 8;

d_вх = D_вх 100 % / N = 0,049 %;

g_вх = D_вх 100 % / N_N = 0,012 %.

 

1.14. Вольтметр V1 класса точности 1,0 с диапазоном показаний (0…100) В и вольтметр V2 класса точности 2,0 с диапазоном показаний (–50…50) В подключены к одному источнику напряжения. Измерения проводятся при нормальных условиях, погрешности отсчитывания пренебрежимо малы. U₁ = 45,6 В и U₂ = 47,5 В — показания V1 и V2 соответственно. Можно ли утверждать, что хотя бы один из вольтметров не отвечает указанному для него классу точности?

 

Решение:

Нет, так как: U₁ – U₂ = (U_и + D₁) – (U_и + D₂) = D₁ – D₂;

– D_о.п1 – D_о.п2 £ D₁ – D₂ £ D_о.п1 + D_о.п2;

½U₁ – U₂½_max = D_о.п1 + D_о.п2 = 0,01 ^. 100 В + 0,02 ^. 50В = 2,0 В;

½U₁ – U₂½ < ½U₁ – U₂½rong>50В = 2,0 В;

½U₁ – U₂½ < ½U₁ – U₂½_max.