Вопросы и задания для самостоятельной работы 3 страница

На основе логико-дидактического анализа темы сложения можно

сразу выделить основные случаи вычитания: 45 — 5, 45 — 40,

— 20.

(1) 40—20.

Этот прием естественно формировать у учащихся одновременно

приемом сложения круглых десятков. Разность 40—30 рассматривается как разность однозначных именовннь1х чисел: 4 дес. — З дес.= 1 дес., т. е. 40—30= 10.

(2) 45 —5 и 45—40.

Эти приемы рассматриваются при знакомстве учащихся с нумерацией двузначных чисел типа 21, 22, 23 и т. д. Они, так же как и при-

сложения для сумм вида 40+5, основываются на знании учащихся разрядного Состава двузначных чисел. Этим обусловлена воз)ЖНОСТЬ одновременного изучения данных приемов сложения и 1читания. Приемы (1) и (2) не требуют средств наглядности.

Раскроем содержание приемов, которые иллюстрируются с помощью абака.

(3) 45—З.

На абаке изображено уменьшаемое 45. Число З вычитается из числа единиц уменьшаемого

(4О+5)_З_ прием (2);

4О+(5_З)40+2прием (2)

(4) 40—5.

На а не изображено уменьшаемое. Согласно правилу работы с абаком, 1 из 4 полосок заменяется 10 квадратами и 5 из них удаляются. Математически это записывается так:

______ —прием (1);

=ЗО+(IО_5)=30+5прием (2).

(5) 45—9.

В абаке находятся 4 ПОЛОСКИ и 5 квадратов. Сначала из него играют 5 квадратов. Остальные 4 квадрата удаляются так же, как в случае 40—5:

— прием (2); =40-_-436 —прием (4).

(6)

На абаке изображено уменьшаемое 45. Очевидно, что нужно удалить З ПОЛОСКИ. Это выражается следующей записью:

(40+5)—30 —прием (2);

(40—З0)+5 —приём (1

=10+5—_прием (2).

(7)

Числу 45 в абаке соответствуют 4 полоски и 5 квадратов, а числу 23—2 полоски и З квадрата. Поэтому из абака удаляются 2 полоски и З квадрата:

45—(20+З)= —прием (2);

=(4)_-3== —прием (б);

=(25—3)— прием (3).

(8) 45—28.

В абаке находятся 4 полоски и 5 квадратов. Исходя из разрядного состава вычитаемого, удаляют 2 полоски и 8 квадратов. Математически это записывается так:

45—(20+8)= —прием (2);

=(45—20)----8= —прием (б);

=25—8—прием (5).

Теперь можно построить схему, отражающую связи между рассмотренными приемами (рис. 20). Схема позволяет определить разные варианты порядка изучения

приемов вычитания. Выше было установлено, что целесообразно рассмотреть с учащимися сначала прием (1), а затем прием (2), причем в связи с соответствующими приемами сложения.

Методически целесообразно также изучать приемы вычитания (3) и (б) одновременно с нумерацией двузначных чисел вида 21, 22, 23... Это позволит закрепить знания учащихся о позиционном значении цифр в двузначном числе.

Труднее обосновать порядок изучения приемов (4), (5), (7) и (8). Возможны варианты — (4, 5, 7, 8), (7, 4, 5, 8), (4, 5, 8, 7). Остановимся на такой последовательности: (4)—(5)-----(7)—(8).

Итак, с помощью логико-дидактического анализа обоснован следующий порядок изучения сложения и вычитания в связи с изучением нумерации чисел в пределах 100:

Вприемах вычитания используются правила вычитания числа из суммы (см. приемы (3), (4), (6)) и вычитания суммы из числа (см. приемы (5), (7), (8)). Они изучаются по такому же плану, что и правила прибавления числа к сумме и суммы к числу.
1. На уроке рассматривается текстовая задача, математическое содержание которой описывается выражением вида (а + Ь) — с (где а и Ь больше с) или т — (п + р). Затем условие этой задачи изменяется в соответствии с выражениями (а — с) + Ь и (Ь — с) + а или (т—п)—р и (т—р)----п.
Например, для обоснования правила вычитания числа из суммы может быть предложена такая задача: «У мальчика было 8 синих и б красных воздушных шаров. Он отдал сестре 4 шара. Сколько шаров осталось у мальчика?» Выясняется, что задаче соответствует выражение (8+6) —4.
Если условие этой задачи конкретизировать «У мальчика было 8 синих и б красных воздушных шаров. Он отдал сестре 4синих шара. Сколько шаров осталось у мальчика?» или «У мальчика было 8 синих и б красных воздушных шаров. Он отдал сестре 4 красных шара. Сколько шаров осталось у мальчика?», то исходное выражение принимает следующий вид: (8 — 4) + б или (6 — 4) + 8. С помощью иллюстрации на наборном полотне легко показать, что ответ не изменяется, т. е. (8+6) —4= (8—4) +6= (6—4) +8.
2. Учащимся предлагаются числовые выражения вида (а + Ь) — с, (а—с)+Ь, (Ь—с)+а или т—(п+р), (аг—п)---р, (т—р)—п, по которым необходимо составить три задачи, имеющие похожий сюжет иодинаковые числовые данные.
Цель этой работы состоит в том, чтобы, с одной стороны, показать учащимся реальный характер отношений (а + Ь) — с = (а —— с) + Ь =
и iп—(п+р)_—(,ч-—п)—р=(т—р)—а. С другой стороны, школьники должны увидеть, что данные правила можно «вспомнить», если составить, а затем переформулировать условие задачи. Последнее особенно важно, если иметь в виду опасность заучивания этих правил учащимися.
3. Наконец, правило отрабатывается на системе целесообразных упражнений.
Рассмотрим методику обучения учащихся вычислительным приемам в пределах 100. Изучение каждого приема осуществляется по следующему плану. На демонстрационном абаке выполняются действия, раскрывающие суть приема. Под руководством учителя учащиеся дают пояснения действиям с абаком, которые позволяют сформулировать их на математическом языке — записать на доске в виде числовых выражений.
Рассматривается аналогичная сумма (разность). Учитель на демонстрационном абаке, а учащиеся на индивидуальных абаках одновременно выполняют преобразования. Математические выражения записываются на доске и в тетрадях.
дальнейшая работа над вычислительным приемом проводится без абака, с полной или сокращенной записью промежуточных действий в тетрадях, с проговариванием этих действий вслух или про себя.
При этом учащиеся Пользуются Соответствующей терминологии «разложу уменьшаемое на разрядные (удобные) Слагаемые>, «вычту ЧИСЛО из суммы>, «прибавлю ЧИСЛО к сумме> и т. п.
Приведем ВОЗМОЖНЫЙ диалог учителя с учеником при Изучении приема Вычитания однозначного числа ИЗ круглых десятков.
На доске Записано число 30.
Учите л Ь: Как Изобразить ЧИСЛО ЗО на наборном Полотне?
Учен и к: В З Кармашка нужно ПОЛОЖИТЬ ПОЛОСКИ, Обозначающие десятки.
Уч и т ел ь: Из числа ЗО нужно вычесть 4. Как изобразить на наборном Полотне, что вычитается 4?
Уч е н и к: Вычесть 4 единицы — это значит убрать 4 Квадрата.
Уч и т ел ь: Но ведь в кармашках Содержатся ТОЛЬКО ПОЛОСКИ.
Уче н и к: Каждую Полоску МОЖНО заменить 1О Квадратами.
Уч и т ел ь: Нужно ли все ПОЛОСКИ заменять квадратами? Быстро с такой задачей не справиться...
Учен и к: Убирается всего 4 квадрата, значит, достаточно заменить Квадратами ТОЛЬКО Одну полоску.
Все эти операции ВЫПОЛНЯЮТСЯна демонстрационном абаке и после того, как убраны 4 квадрата, подсчитывается ответ.
Учащиеся проговаривают выполняемые действия, учитель с помощью учащихся выполняет на доске соответствующие записи.
В Заключение сделаем два Замечания
1. Изучая приемы устного сложения двузначных чисел, учащиеся должны прийти к выводу, что СЛОЖИТЬ два двузначных Числа легче, если к десяткам первого прибавить число Десятков Второго, единицы обоих слагаемых сложить и прибавить к сумме Десятков. для того чтобы этот прием был эффективен, учащиеся должны хорошо знать таблицу сложения.
2. Кроме рассмотренных ОСНОВНЫХ Приемов, полезно показать учащимся некоторые частные приемы, Основанные на связи между компонентами и результатами операций. Пусть, например, складываются числа 39 и 46. Замечают, что 39— это 40 без одного. К 40 прибавить 46 легко, получается 86. Но одно из слагаемых было увеличено на единицу, поэтому Сумму нужно на единицу уменьшить: 86 1 85.
Аналогично поступают, если, например, к 58 прибавляется 37.
К первому слагаемому добавляют 2 единицы, а от полученной
суммы 97 вычитают 2.
Более сложные рассуждения используются для объяснения аналогичных приемов вычитания, например 65—39: «Вычитаемое увеличиваем на единицу: 65—40. Но от этого разность уменьшается на единицу, поэтому к 25 нужно прибавить 1з.
Умножение и деление.Усвоение учащимися нумерации чисел в пределах 1оо открывает возможности для обучения их табличному умножению и делению. Изучение операций умножения и деления в концентре «Сотня» предполагает усвоение учащимися таблицы умножения однозначных чисел и соответствующих случаев деления. Кроме того, ученики должны усвоить приемы устного Умножения и деления в случаях, не являющихся табличными.
Табличное умножение и деление. Изучение этой темы осуществляет по следующему плану:
1) раскрывается СМЫСЛ операций умножения и деления;

2) учащиеся усваивают особые Случаи умножения и деления (единицы и нуля, на единицу и нуль).

3) изучаются таблицы умножения чисел 2, 3, 4, 5, 6, 7, 8, 9 на однозначные числа и соответствующие случаи деления.

Из вузовского курса математики известны два подхода к определению произведения натуральных чисел — через декартово произведение множеств и аксиоматическое (определение через сложение). В начальной школе ни один из этих подходов невозможно осуществить в полном объеме. Однако возможно использование их некоторых элементов. Так, умножение в начальных классах определяется через сложение (деление — через умножение). Главным же средством наглядности при изучении умножения является таблица, иллюстрирующая декартово произведение двух множеств.

Как и все основные математические понятия в начальной школе,

умножение и деление вводятся с помощью системы целесообразных задач с последующей математизацией их содержания.

При знакомстве с операцией умножения учащимся могут быть предложены, например, следующие задачи.

Задача 1. Автомобиль «Волга может одновременно перевезти 4 пассажиров. Сколько людей смогут перевезти за одну поездку З автомобиля «Волгах.?

Задача 2. Ученик купил 5 тетрадей и заплатил за каждую 2 к. Сколько всего денег заплатил ученик?

Задача З. Масса 1 пакета картофеля —З кг. Хозяйка купила З таких пакета. Сколько килограммов картофеля она купила?

Особенность таких задач состоит в том, что учащиеся могут легко обнаружить в условии одинаковые слагаемые. Встречающиеся в них величины должны быть хорошо знакомы учащимся и допускать наглядную иллюстрацию.

Формулируется задание: записать выражения к задачам. Уже при изучении таблицы сложения учащиеся встречались с суммами, имеющими более двух слагаемых, два или более одинаковых слагаемых. Поэтому данное задание не должно вызывать у них затруднений.

Записан соответствующие выражения (4+4+4, 2+2+2+2+ +2, 3+3+3), учитель сообщает учащимся, что эти суммы можно записать иначе с помощью умножения: 4 3, 2 5, 3• 3. Первый множитель показывает, чему равно каждое слагаемое в сумме, а второй — сколько слагаемых в сумме. Точка обозначает действие

умножение. Выражение вида 4 3 называется произведением. Таким образом, решение приведенных выше задач можно записать в виде

СУММЫ и произведения.

Целесообразно предложить учащимся самим придумать задачи, решаемые умножением, либо составить задачи по данным выражениям: 5+5+5+5 и 5.4, 7+7 и 7.2, 14+14+14+14 и 14.4 ит.д.

При работе над задачами выполняются различного рода иллюстрации. Например, может бы?ъ использована прямоугольная табли

ца, которая позволяет наглядно представить декартово произведение двух множеств. Таблицу (рис. 21) можно сделать из фанеры. Ряды и столбцы таблицы нумеруются. Размеры «окон определяются с таким расчетом, чтобы в них можно было закрепить рисунки. Задача может быть решена умножением, если заполненная часть таблицы имеет вид прямоугольника. Так, например, рис. 22 иллюстрирует задачи 1 и 2.

После содержательных задач учащимся предлагаются числовые выражения суммы, которые необходимо представить в виде произведения. Так как учащиеся при вычислении произведений пользуются сложением, слагаемые в этих суммах могут быть и двузначными: 30+30+30, 25+25+25+25 и т. д.

Выполняются также задания другого рода: «Представить в виде суммы следующие произведения: 2.4, 15 .3, 4 2» и т. д.

Тема «деление» в методическом отношении более сложная, чем «Умножение И это естественно: вводи операцию умножения, учитель опирается на хорошо усвоенную учащимися операцию сложения, на отработанные вычислительные навыки. деление же нельзя определить через умножение, поскольку и умножение является для учащихся новой операцией. Таким образом, роль содержательных задач, наглядных пособий при введении деления еще более значительна, чем при умножении.

Методика обучения решению таких задач будет раскрыта в § 20. Сейчас же покажем возможности использования демонстрационной таблицы для раскрытия смысла деления.

Рассмотрим, например, следующие задачи.

Задача 4. для одновременной перевозки 12 человек выделено несколько автомобилей «Волга». Одна «Волга» может взять 4 пассажиров. Сколько автомобилей было выделено для перевозки?

Задача 5. Ученик купил 5 одинаковых тетрадей и заплатил 10 к. Сколько стоит одна тетрадь?

Задача б. Масса 1 пакета картофеля составляет З кг. Хозяйка купила 9 кг картофеля. Сколько пакетов она купила?

Решаются эти задачи с использованием наглядных пособий. Так, 12 кружков, которые соответствуют количеству пассажиров из 4, раскладываются группами по 4, а затем подсчитывается количество групп; 10 квадратов (задача 5) раскладываются по 5 и подсчитывается, сколько групп квадратов получилось, и т. д.

Этими же геометрическими фигурами заполняется демонстрационная таблица. Например, 12 отобранных для задачи 4 кружков располагаются в строках таблицы: в первой строке — 4 кружка (количество пассажиров в первой машине); во второй — 4 и т. д. Обращается

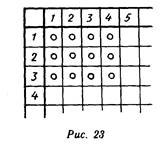
внимание учащихся на то, что в таблице заполнен прямоугольный участок (рис. 23).

Учитель сообщает, что, решая задачу 4, число 12 разделили на 4 и получили в результате число З. деление 12 на 4 записывается так: 12:4. Число 12 называется делимым, 4 — делителем, З - частным.

Сравниваются условия задач 1—З и 4—6. Похожи не только они, схожи и иллюстрации, выполненные с помощью демонстрационной таблицы. Анализ этого сходства позволяет учащимся осознать связь между умножением и делением: если произведение разделить на один из множителей, то получится второй множитель. На практике это может быть достигнуто следующим образом.

Учащимся предлагается задача: К празднику Октября родители купили сыну 4 воздушных шарика. Каждый шарик стоит З к. Сколько денег заплатили родители за шарики? Кратко записывается условие задачи:

Купили — 4 шарика.

Цена — З к.

Заплатили —? к.

Составляется выражение: 3. 4= 12.

Затем предлагается другая краткая запись:

Купили —? шариков.

Цена — З к.

Заплатили — 12 к.

Выясняется, чем вторая задача отличается от первой. Вторая задача называется обратной первой. Записывается ее решение:

12:3=4.

Рассматривается краткая запись еще одной задачи, обратной первой:

Купили — 4 шарика.

Цена — ? к.

Заплатили — 12 к.

Записывается решение: 12:4=3.

делается вывод: 3. 4=12, значит, 12:З=4 и 12:4= 3.

Чтобы подготовить учащихся к изучению таблицы умножения и соответствующих случаев деления, необходимо ознакомить их с переместительным законом умножения и особыми случаями умножения и деления. для этого целесообразно воспользоваться демонстрационной таблицей. Иллюстрируем на ней произведения З . 4 и 4 3

(рис. 24), 2 . 5 и 5 2, легко убедить учащихся, что эти произведения равны — очевидно равенство соответствующих прямоугольников. Здесь же нужно показать, что наученное свойство можно использовать при вычислении значений произведений. Например, до знакомства с этим свойством при вычислении произведения 2. 9 необходимо было подсчитать значение суммы, состоящей из 9 слагаемых. Переместительный закон позволяет упростить вычисления: 2. 9

9. 2, а 9. 2=9+9. Работа над упражнениями такого рода

является хорошей подготовкой к изучению

таблицы умножения.

г Усвоение учащимися переместительного закона умножения позволяет несколько изменить требования к решению задач с помощью умножения.

до изучения этого закона задача 2, например, решалась с помощью выражения 2.5(2 к.. 5=10 к). Выражение 5 . 2 казалось необъяснимым исходя из условия задачи (но, кстати говоря,

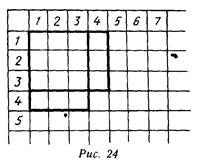
вполне объяснимым, если рассматривать прямоугольную таблицу, см. рис.24). После изучения переместительного закона становится естественным, что оба выражения — 2 . 5 и 5 . 2 — являются решением задачи 2. Причем найти значение 5 . 2 через сумму легче, чем 2 . 5. В ответе же исходя из здравого смысла получают 10 к. Таким образом, наряду с записью 2 к. . 5 = 10 к. возможна запись 5 .2 к. = 10 к.

Особые случаи умножения и деления. Таблица умножения состоит, как известно, из отдельных таблиц умножения числа 2 на однозначные числа, умножения числа З и т. д. Случаи умножения единицы и десяти в таблицу не включаются, так как соответствующие результаты не высчитываются — они находятся по достаточно простым правилам. Умножение единицы и на единицу, десяти и на десять, нуля и на нуль, а также соответствующие случаи деления рассматриваются особо.

В вузовском курсе математики свойство а 1 = а формулируется в определении операции умножения. То, что 1 . а = а, доказывается исходя из этого определения. В этом же курсе правило умножения нуля и на нуль доказывается исходя из определения нуля и свойств операции умножения. деление нуля и невозможность деления на нуль обосновываются с помощью определения деления и умножения нуля на число.

В начальной школе такой подход к разъяснению особых случаев умножения и деления невозможен. Попытка обосновать, что а 1 = а и а 0= 0, опираясь на определение умножения через сумму, также невозможна: непонятно, что есть «сумма», у которой только одно слагаемое, или «сумма» без слагаемых. Поэтому эти случаи умножения, а также правило «на нуль делить нельзя» учащиеся должны просто запомнить.

Правила умножения единицы и нуля объясняются через сложение: 1. 4=1+1+1+1=4, 0. 5=0+0+0+0+0=0 и т. д.

клетки (рис. 27). На первых порах с помощью этих прямоугольников подсчитываются значения произведений и частных. Они используются также для иллюстрации переместительного закона умножения, при изучении таблиц умножения трех, четырех и т. д.

Заучить таблицу умножения двух можно в результате многократного вычисления произведений и соответствующих частных. для этого необходимо использовать содержательные задачи. С одной стороны, они вносят разнообразие в работу, предупреждают зазубривание таблицы, с другой — учащиеся видят практическую значимость таблицы, необходимость ее запоминания.

Аналогично происходит знакомство с таблицами умножения трех, четырех, ..., девяти:

значения табличных произведений, соответствующих частных подсчитываются через сумму с помощью демонстрационной таблицы, прямоугольников;

анализируются связи между 5езультатами, уже полученными в данной таблице, различные способы их получения;

при работе над табличными случаями умножения и деления используются содержательные задачи;

для построения каждой новой таблицы используются результаты ранее изученных таблиц; за счет этого количество рассматриваемых случаев в каждой последующей таблице уменьшается.

Например, при построении таблицы умножения трех случай

3. 2 не рассматривается как новый этот результат был получен

в таблице умножения двух. При построении таблицы умножения

четырех не подсчитываются произведения 4. 2 и 4. 3. Таким образом, таблица умножения девяти содержит только один новый случай—9. 9

Уменьшение количества новых случаев от таблицы к таблице позволяет, с одной стороны, увеличить время на изучение новых таблиц и на закрепление уже изученных. С другой стороны, больше внимание уделяется решению задач, требующих знания таблицы умножения.

Внетабличное умножение и деление. Случаи умножения однозначного числа н однозначное являются табличными.

Таким образом, к внетабличным случаям относится умножение двузначного числа на однозначное. Прием устного умножения должен основываться на знании учащимися таблицы умножения. Поэтому двузначные множители необходимо привести к такому виду, который допускал бы использование таблицы умножения. для этого двузначные множители представляются в виде суммы разрядных слагаемых (одно из слагаемых однозначное число, второе

круглые десятки). При сложении и вычитании круглых десятков использовался прием замены круглых десятков однозначными именованными числами. Таким же образом умножение и деление круглых десятков на однозначное число может быть сведено к умножению однозначного именованного числа на однозначное: 40. 2 — 4 дес. 2 = 8 дес., т. е. 40 . 2 = 80. Умножение двузначного числа на однозначное выполняется так:

24 . 3= (20 + 4) .3 20 .3 +4 .3 60 + 12.

Операцию разложения числа на разрядные слагаемые учащиеся выполняют устно. К этому времени они умеют устно находить произведение однозначных чисел, сумму двузначных чисел. Поэтому для того чтобы сформировать у учащихся умение устно умножить двузначные числа на однозначные, необходимо ознакомить их еще с двумя операциями: умножением суммы на число и умножением круглых десятков на однозначное число. Методика изучения последней операции, как было показано выше, весьма проста, поэтому остановимся подробно на методике обучения умножению суммы на число.

Умножение суммы на число. Методика изучения этой темы (как и изучение всех математических понятий в начальной школе) основывается на использовании системы целесообразных задач, наглядных интерпретациях их содержания. Чтобы выяснить их особенности, воспользуемся определением умножения через сумму для случая, когда один из множителей представлен суммой:

(а+Ь)..с=(а+Ь)-.-(а+Ь)-4.-...--(а+Ь).

с раз

Правую часть этого равенства графически можно представить в виде с рядов объектов одного рода, причем в каждом ряду содержится а объектов одного вида и Ь объектов другого. В качестве таких объектов можно взять кружки двух видов светлые и темные (рис.28).

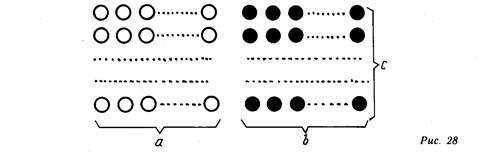
В соответствии с таким рисунком легко составить содержательные задачи, являющиеся средством формирования правила умножения суммы на число. Например: «В пионерском отряде 4 звена. В каждом звене 5 девочек и 4 мальчика. Сколько всего пионеров в отряде?», «На субботнике по благоустройству школьного двора каждому октябрятскому отряду было поручено посадить по 2 клена и по З липы. Сколько всего деревьев должны были посадить 5 отрядов?» и т. д.
• Для каждой из таких задач составляются выражения двух видов (в соответствии с двумя возможными способами их решения), которые также можно проиллюстрировать графически:
(5+4)•4 54+4•4
(2+3).5 2.5+3.5 и т. д.
Соответствие двух разных выражений одной и той же конкретной ситуации делает факт равенства этих выражений очевидным.
Затем учащимся предлагается самостоятельно составить содержательные задачи по выражениям вида (а + Ь). с и а• с + Ь . с.
В заключение прием умножения суммы на число отрабатывается на числовых выражениях. Упражнения подбираются так, чтобы ученики могли выбрать наиболее удобный способ вычислений. Например, значение выражения (2 + 4). 6 удобнее вычислять как произведение (умножение б . б табличное) Значение выражения (9+5).8 определяется в три действия: 9•8+5.8, поскольку умножить 14 на 8 учащиеся еще не умеют.
Правило умножения числа на сумму особо можно не рассматривать. Пользуясь переместительным законом умножения, младшие школьники самостоятельно могут преобразовать выражение (9+ + 5) 8 к виду 8 (9 + 5). Если же учитель найдет нужным подробно остановиться на содержании этого правила, то методика его изучения аналогична методике, рассмотренной выше.
Алгоритм умножения двузначного числа на однозначное можно
представить в виде последовательности операций: (1) - двузначный Ь— множитель представляется в виде суммы разрядных слагаемых;
(2) сумма умножается по правилу умножения суммы на число;,
(3) вычисляется произведение круглых десятков на число; (4) -
определяется произведение однозначных чисел; (5) — вычисляется полученная сумма. Например:

На первых порах от учащихся можно требовать комментирования отдельных шагов алгоритма.
деле н и е. При изучении деления в пределах 100 ученики должны овладеть приемами деления двузначных чисел на однозначные (в случаях, не являющихся табличными: 36:2, 45:3, 76:4 и Т. д.) И двузначных и двузначные.
Частные, в которых делитель однозначное число, с методической точки зрения не оноронь1. Например, при делении 42 на 2
может быть использован прием, похожий на прием устного умножения: (40+2):2=40:2+2:2. Однако для случаев 84:3, 51:3, 30:2 такой прием нельзя применить.
Таким образом, нужен такой прием устного деления, который был бы пригоден для всех случаев, когда делимое двузначное, а делитель — однозначное число. Очевидно, что в основе такого приема должно лежать разложение делимого на слагаемые, каждое из которых делится на делитель. В связи с этим учащихся необходимо предварительно ознакомить с правилом деления суммы на число: (а+ +Ь) :с.
Деление суммы на число. Вначале изучения данной темы учащимся предлагается система целесообразных содержательных задач, например таких: «В одной вазе б слив, а в другой — 8. Эти сливы разделили поровну между двумя мальчиками. Сколько слив получил каждый мальчик?»; «Ученик купил тетради в линейку и клетку по цене З к. За тетради в линейку он уплатил 12 к., за тетради в клетку — б к. Сколько тетрадей всего купил ученик?»; «В два ларька привезли ящики с черешней по 4 кг в каждом. В один ларек привезли 12 кг черешни, а в другой — 24 кг. Сколько ящиков с черешней привезли в оба ларька?» и т. д.
Под руководством учителя иллюстрируются два способа решения каждой задачи: (6+8) :2 и 6:2+8:2; (12+6):2 и 12:2+6:2; (12+24) :4 и 12:4+24:4.
Так как каждое из двух выражений соответствует одной и той же реальной ситуации, то равенство их значений не вызывает сомнений.
Обобщение двух способов решения разных по содержанию задач подводит к формулировке правила: чтобы разделить сумму на число, нужно на это число разделить первое и второе слагаемые и полученные результаты сложить.
Рассматривается система упражнений вида (а + Ь): с ==? В одних случаях значение частного удобнее найти, не преобразуя частное, а в ‘других случаях — используя изученное правило. При этом школьники могут проговаривать правило, однако требовать его запоминания, очевидно, не стоит.
деление двузначного числа на однозначное. Вначале предлагается самый простой вид внетабличных частных:
е— 24:2, 33:3, 36:3, 48:4 и т. д. Школьники могут самостоятельно прийти к выводу, что деление в данных случаях можно выполнить с помощью приема, очень похожего на прием устного умножения: делимое представляется в виде суммы разрядных слагаемых, и деление выполняется по правилу деления суммы на число.
Затем ученикам предлагаются частные, для которых этот прием неприменим: 78:3, 32:2, 92:2 и т. д. Одновременно учитель приводит доказательство того, что в каждом из этих случаев значение частного существует: 78:3= 26, так как 26. 3=78; 32:2= 16, так как 16. 2=32 и т. д.
Используя опыт деления суммы на число, учащиеся могут предложить (к этому их нужно побудить, подтолкнуть) разложить делимое на удобных’ слагаемые, делящиеся на делитель. На конкретных примерах демонстрируется трудоемкость этого приема. Пусть, например, делимое 78 представлено в виде суммы 21 +57, тогда процесс деления будет таким:
78 : 3= (21 +57) : 3= 21 :3+ 57 : 3=
внетабличное деление
=7+(21+36):3=7+21:3+363=
внетабличное деление
=14-+(30+6):3=14+10+2=26.
Прием разложения делимого на «удобные» слагаемые использовался в данном случае неоднократно. Возможно, что делимое было представлено не лучшим образом. Было бы легче, если бы оно было заменено суммой, в которой первое слагаемое являлось круглыми десятками, делящимися на делитель, например 60 или 30.
Затем рассматривается частное, в котором делимое представлено суммой, одно из слагаемых которой круглые десятки, делящиеся на делитель. Причем замена делимого суммой выполняется различными способами:
96:3=(30+66):3==30:3+66:3=10+(30+36):3==10+30:
:3 + 36:3
96:3= (60+36):3=60:ЗЧ-36:3=20-I-(30-i-6):3=20+30:3+
+ 6:3 = 20+10+2 = 32
96:3=(90+6):3=90:3+6:3= 30+2=32.
Очевидно, что самый простой случай — третий. Его особенность состоит в том, что одно из слагаемых не просто круглые десятки, делящиеся на делитель, а наибольшее количество десятков, делящихся на делитель.
На конкретных примерах доказывается действенность разработанного приема (в числе примеров встречаются и частные вида 30:2, 50:2, 60:4, 60:5 и т. д.). При делении учащиеся могут проговаривать отдельные операции алгоритма: (1) делимое заменяется суммой, где одно из слагаемых наибольшее количество десятков, делящихся на делитель; (2) -- сумма делится по правилу деления суммы на число; (3) вычисляется частное круглых десятков на число; (4) вычисляется табличное частное; (5) вычисляется полученная сумма.
Деление двузначного числа на двузначное. В начальных классах значение частного двузначных чисел определяется При этом используются знания учащихся о связи между умножением и делением: если частное подобрано верно, то при умножении его на делитель должно получиться делимое. Отметим, что вопрос о том, сколько цифр должно иметь частное, с учащимися не обсуждается.
Приступая к изучению приема деления двузначного числа на двузначное, учитель предлагает учащимся достаточно простые частные, значения которых учащиеся в состоянии угадать, например 20:10, 60:30, 80:20,80:40и т. д.
Затем учащимся предлагается доказать, что угаданное значение
108