Вопросы и задания для самостоятельной работы 2 страница
СОТНЯ
Нумерация и сравнение чисел в пределах 20.Вначале повторяются некоторые вопросы нумерации чисел до 10: получение следующего числа натурального ряда прибавлением числа 1, сравнение соседних чисел, имена чисел в устной и письменной нумерации. Обращается внимание учащихся на то, что имена чисел от О до 9 не связаны друг с другом: для обозначения чисел от О до 9 на письме используются особые знаки, не связанные структурно с другими знаками; в устной речи числа от О до 9 обозначаются отдельными словами, каждое из которых не зависит от других слов.
Изучение устной нумерации чисел от 10 до 20 начинают с ознакомления учащихся с понятием Выполняя различные упражнения на счет предметов, ученики объединяют эти предметы в отдельные группы по 10 штук — пучки палочек, связки колечек и т. д. Затем вводится понятие десятка: десять предметов образуют десяток.
Работу на уроке по введению чисел от 11 до 20 можно организовать так. Учитель спрашивает: «Как получить число, следующее за числом 10?. Ученики отвечают: «К 10 прибавить 1». На десять предметов — десяток — кладется еще один предмет. Сколько сейчас предметов? Получив ответ: Одиннадцать»* учитель обращает внимание на структуру этого слова: один-на-дцать, указывая, что «дцать» является сокращением слова «десять»**. Подобным образом вводятся все числа до 19. дети получают представление об образовании чисел от 11 до 19, одновременно
Наконец, вводится число 20. Имея один десяток предметов и еще 9 предметов, учитель добавляет к ним один предмет, затем объединяет новые десять предметов в новый десяток и спрашивает у учащихся, сколько получилось десятков. Затем изучается десятичный состав этих чисел. Первые упражнения выполняются с использованием дидактического материала, который в дальнейшем постепенно исключается. Решаются такие типы упражнений.
1. Отсчитайте 16 предметов, отделите 10 предметов (выделите десяток). Сколько десятков в числе 16? Сколько единиц в числе 16 (сверх десяти)? Сколько всего единиц в числе 16?
2. Отсчитайте один десяток предметов, затем добавьте еще З предмета. Сколько всего предметов отсчитали? Сколько десятков и сколько единиц в числе 13? Сколько единиц в числе 13?
3. Сколько десятков и сколько единиц в числе 17? 15? 20?
4. Какое число составят 1 десяток и 8 единиц? 1 десяток и 1 единица?
После усвоения учащимися устной нумерации приступают к изучению письменной Нумерации. Ознакомление учащихся с позиционным принципом записи чисел второго десятка осуществляется с помощью абака, представляющего собой таблицу с двумя рядами карманов: один из рядов предназначен для палочек, другой для цифр. В дальнейшем при изучении нумерации используют таблицу разрядов с надписями справа налево: «единицы», «десятки», а также таблицу с двумя подвижными лентами с записанными на них цифрами. Учащиеся сами изготавливают подобные пособия.
Приступая к объяснению принципа записи чисел второго десятка, учитель подчеркивает, что при этом используются те же знаки, что
и для обозначения чисел первого десятка цифры 0, 1, 2, 3, 4, 5, 6, 7,
8, 9. Затем учитель называет некоторое число, например 14. Вместе
с учащимися выясняется десятичный состав этого числа: 1 десяток
и 4 единицы. Затем в верхний ряд карманов вставляются слева
десяток палочек, связанных пучком, а справа 4 палочки, в НИЖНИЙ
ряд — цифры 1 и 4. Получается обозначение числа четырнадцать.
Выполняются и такие упражнения:
1) учитель на абаке обозначает число цифрами, учащиеся иллюстрируют его палочками и записывают на доске;
2) учитель на абаке обозначает число палочками, учащиеся обозначают его цифрами и записывают имя числа на доске;
3) учитель записывает число на доске. Учащиеся его читают называют число десятков и число единиц;
4) учитель называет число. Учащиеся записывают его и называют число десятков и число единиц.
* Если никто из учащихся не знает названия этого что маловероятно, учитель сообщает его сам.
** В переводе с древнерусского одиннадцать означает один сверх десяти Рассматривается запись чисел 10 и 20, уясняется, что в этих записях цифра 1 (или 2) показывает, что в данном числе содержится
1 десяток (или 2 десятка), а цифра О — что эти числа не содержат
единиц сверх тех, что образуют десятки. Могут быть использованы
и упражнения другого характера:
1) запишите число, следующее за числом 12;
2) запишите число, предшествующее числу 20;
3) вычислите: 13+1; 13—1.
При изучении нумерации чисел второго десятка учащиеся знакомятся со случаями прибавления и вычитания числа 10, прибавления
к 10 и вычитания из числа всех его разрядных единиц, закрепляют
свойства числа О : а + 0, а —. Например, при решении упражнения
19—9 рассуждают следующим. образом: 19 содержит 1 десяток и
9 единиц, если вычесть 9 единиц, то останется 1 десяток, т. е. 10. Особое внимание уделяется введению понятий: однозначное число», «двузначное число». Учащиеся видят, что для записи чисел, состоящих только из единиц, требуется одна цифра, а для записи чисел, состоящих из десятков или десятков и единиц,— две цифры. После этого вводятся термины: «однозначное число», «двузначное число». для закрепления введенных понятий выполняются такие упражнения:
1) записать З однозначных и З двузначных числа;
2) из множества чисел 0, 20, 11, 2, 7, 15, 10, 2, 12 выписать сначала однозначные, а затем двузначные числа. Записать их в порядке возрастания (убывания);
3) записать З однозначных числа. Увеличить каждое из них на 10. Какие числа получились? Как можно их назвать?
4) записать З двузначных числа, не равных 20. Уменьшить их на 10. Какие числа получились? Как можно их назвать?
5) с помощью цифры 1 записать однозначное и двузначное числа. Что означает цифра 1 в записи числа II?
Нумерация и сравнение чисел в пределах 100.Знакомство с числами от 21 до 100 начинают с устной нумерации. Образование и называние чисел 30, 40, 50, 60, 70, 80, 90, 100 объясняется в процессе счета десятками: 1 десяток — десять единиц, 2 десятка — двадцать единиц, З десятка — тридцать единиц, 4 десятка сорок единиц, 5 десятков — пятьдесят единиц, шесть десятков шестьдесят единиц, семь десятков — семьдесят единиц, восемь десятков — восемьдесят единиц, девять десятков — девяносто единиц, десять десятков — сто единиц. При введении и анализе названий десятков обращается внимание на то, что все они, кроме «сорок» и «сто», образованы по одному принципу. Правда, слово «десять» претерпело разные изменения в группе «двадцать-тридцать» и в группе «пятьдесят- шестьдесят-семьдесят-восемьдесят». На ранних ступенях развития русского языка вместо «сорок» и «сто» говорили «четыредесять» и «девятьдесять». Поясняя происхождение слова «сорок», полезно сов ершить экскурс в историю*.
* Тридцать образовалось как и двадцать ‘пятьдесят образовано в результате сращения спять десять — пять десятков; подобным образом образовались шестьдесят*, семьдесят, восемьдесят девяносто встречается в памятниках
84
Освоив счет десятками, учащиеся знакомятся с образованием итенами Любых чисел в пределах сотни: 2 десятка и 5 единиц — это двадцать пять; 4 Десятка и 7 единиц — это сорок семь и т. п. Упражнения на образование чисел чередуются с упражнениями на разложение чисел: пятьдесят шесть — это 5 десятков и шесть единиц; Девяносто один это 9 десятков и 1 единица и т. п.
При изучении письменной нумерации учащиеся знакомятся с понятиями разряда и разрядного числа. Поясняется, что, например, тридцать семь — это З десятка и 7 единиц, но можно сказать и по-
Другому: З единицы второго разряда и 7 единиц первого разряда. Здесь полезно использовать карточки с разрядными числами, которые Помогают Усвоить состав числа, представить его в виде суммы разрядных слагаемых (56=50+6). Эти навыки затем используются при изучении Операций над натуральными числами.
Изучая нумерацию в пределах 100, учащиеся выполняют упражнения на сложение и вычитание:
1) прибавление и вычитание числа 1;
2) прибавление к целому числу десятков однозначного числа;
З) вычитание всех десятков из числа;
4) прибавление целого числа десятков к однозначному числу;
5) вычитаНие всех единиц из числа.
Методика вычислений здесь та же, что и для Подобных случаев
в пределах 20. При выполнении упражнений на присчитывании
и отсчитывании единицы, чисел, кратных 10, используется наглядное
пособие «лента ста» --— метровая лента с обозначенными сантиметрами и дециметрами
Усвоению Последовательности чисел первой сотни в натуральном ряду способствуют также следующие упражнения:
1) назовите число, предшествующее Числу 27 (после какого числа при счете Называют число 27?)
2) Назовите Число следующее за числом 27 (перед каким числом при счете называют число 28?);
З) между какими Числами называют при счете число 27? -
Работа по усвоению нумерации продолжается и при изучении операций сложения и вычитания в пределах 100.
Итак, изучив нумерацию чисел в пределах 100, учащиеся должны усвоить: а) имена двузначных чисел в устной и Письменной речи, их десятичный состав; б) расположение чисел до 100 ‘в натуральном ряду; в) смысл терминов: «единица первого разряда», «единица второго разряда», «разрядное число», «Однозначное число», «Двузначное число».
Сложение ивычитание. При изучении Операций сложения и вы-
с ХiУ в. как вытеснившее общеславянское «девять-десять» которое сохранилось в других славянских языках, кроме восточнославянских, происхождение «девяносто» неясно; «сто» является общеславянских словом индоевропейского характера; «сорок» используется в восточнославянских языках, пришло на Смену «четыре Десять», возникло на базе Слова «сорок» — «мешок, рубаха» из-за обычая продавать соболиные шкурки сороками с 40 шкурками; таким образом, «сорок» — сначала «мешок», затем «мешок с сорока соболиными шкурками» и, наконец, «сорок) — обозначение четырех десятков.
Вычитания в концентре «десяток» учащиеся должны усвоить главным образом таблицы сложения и вычитания в пределах десяти, В концентре «Сотня» ученики должны овладеть приемами устных вычислений. Эти приемы в дальнейшем используются при устном сложении и вычитании в пределах тысячи, миллиона.
Целесообразность методики обучения вычислительным приемам можно оценить по следующим характеристикам: 1) приемы должны допускать иллюстрацию с помощью наглядных пособий; 2) количество приемов сложения и вычитания в пределах ста должно быть минимальным, а необходимость изучения того или иного приема
методически обоснованной.
Рассмотрим методику обучения учащихся приемам устного сложения и вычитания, удовлетворяющую этим характеристикам.
Выбор вычислительных приемов в начальной школе в значительной мере определяется возможностями наглядной иллюстрации их сущности. Основным наглядным пособием при изучении чисел от 10 до 100 является абак. Удобен абак следующей конструкции: наборное полотно с горизонтальными «карманами», в которые укладываются одинаковые по размеру вырезанные из картона квадраты (единицы) или полоски, состоящие из 10 квадратов (десятки). В каждом кармане можно разместить не более 10 квадратов (одну полоску).

Иллюстрация вычислительных приемов с помощью абака предполагает наличие у учащихся некоторого опыта работы с этим наглядным пособием. Абак может использоваться уже в концентре «десяток», а также в дальнейшем, когда изучаются темы, связанные с нумерацией, арифметическими операциями и сравнением чисел. К началу обучения работе с абаком учащиеся должны уметь устанавливать взаимно однозначное соответствие между элементами двух множеств. Например, откладывать столько кружков, сколько яблок изображено на рис. 13.
Навыки работы с абаком могут отрабатываться при выполнении учащимися, например, следующих систем упражнений.
Первая серия упражнений
Усл о в и е. Учащимся показывают иллюстрации, на которых изображено не более 10 предметов.
Т р е бует с я: изобразить на наборном полотне, сколько всего предметов; сколько предметов останется, если несколько предметов убрать.
Работа над заданиями:
1) учащиеся отбирают столько квадратов, сколько предметов изображено на иллюстрации;
2) отобранные квадраты правильно укладываются в карман наборного полотна: карман заполняется справа налево, квадраты плотно соприкасаются боковыми сторонами. На рис. 14, а квадраты уложены правильно, на рис. i4, б — неправильно;
3) из кармана справа убирают столько квадратов подряд, сколько убрали предметов. На рис. 15, а квадраты убраны правильно, на рис. 15, 6 — неправильно.
Вторая серия упражнений
Усл о в не. Учащимся предъявляется больше 10, но меньше 20 предметов. Т р е бует с я: правильно показать на наборном полотне, сколько всего предметов; сколько предметов останется, если несколько предметов убрать.
Работа над заданием:
i) отбирается столько квадратов, сколько предметов предъявлено;
2) когда отобрано квадратов, в наборное полотно укладывается полоска;
3) остальные квадраты устанавливаются в следующем кармане по уже известному из первой серии упражнений правилу;
(Пусть для определенности было всего 13 предметов, 6, из них убрали.)
4) убираются З квадрата из наборного полотна;
5) чтобы убрать З оставшихся квадрата, полоску в наборном полотне заменяют квадратами и по известному правилу убирают З квадрата.
Третья серия упражнений
У с л о в и е. Демонстрируются рисунки с двумя (тремя, четырьмя) группами предметов разного вида, но одного рода (в совокупности не более 10), например 2 мяча, 1 матрешка и 4 игрушечных автомобиля.
Т р е бует с я: правильно изобразить на наборном полотне, сколько всего игрушек.
Работа над заданием:
1) в карман правильно укладываются квадраты, соответствующие количеству мячей;
2) правильно укладываются квадраты, соответствующие количеству матрешек:
квадраты укладываются в тот же карман, слева направо, начиная от последнего уложенного;
3) правильно кладутся квадраты, соответствующие количеству автомобилей. На рис. 16, а квадраты уложены правильно, на рис. 16, 6 — неправильно.

Четвертая серия упражнений
Усл о в и е. Школьникам предъявляются предметы разного вида (не более 10 каждого), но одного рода, причем в совокупности их более 10.
Т р еб у е т с я: изобразить на наборном полотне, сколько всего предметов. Работа над заданием (предметы трех видов представлены в следующих количествах—5, 7,9):
i) правильно укладываются 5 квадратов, соответствующих количеству предметов первого вида;
2) правильно располагают квадраты, соответствующие количеству предметов второго вида (по правилу, отработанному во второй серии упражнений);
3) по правилам, использовавшимся во второй и третьей сериях упражнений, укладываются квадраты, соответствующие количеству предметов третьего вида. На рис. 17 изображен правильно заполненный абак.
Рассмотренные упражнения (или некоторые из них) могут выполняться как дидактические игры. Учащиеся должны усвоить правила укладки квадратов в карманы абака и удаления их из карманов, замены квадратов полосками и полосок квадратами.
Сложение. для того чтобы выработать подход к изучению определенного учебного материала, в методике используют логикодидактический анализ. Воспользуемся им для определения целесообразной последовательности изучения приемов устного сложения чисел в пределах ста.
Рассмотрим все возможные случаи сумм в зависимости от разрядного состава входящих в них слагаемых: это суммы, у которых значения больше 10 (суммы, равные 10, изучались в концентре «десяток») и не больше 100.
К первой группе можно отнести суммы однозначных слагаемых:
2+9, 3+8 и т. п.
Вторую группу составляют суммы, в которых одно слагаемое двузначное, а другое однозначное: 20+5, 22+5, 28+5 и т. д. Эта группа не является однородной. Найти сумму 22+5 сложнее, чем 20+ 5. Случай же 28+5 (с образованием нового десятка) самый ложный в данной группе.
В третью группу входят суммы двузначных слагаемых. Очевидно, что и эта группа по уровню сложности входящих в нее сумм разделяется на подгруппы. Сложение круглых десятков интуитивно можно оценить как самый простой случай. Сложнее найти сумму, когда одно двузначное слагаемое оканчивается нулем, а второе имеет ненулевой разряд единиц (20+35, 28+40 и т. п.). Затем следуют суммы, у которых оба слагаемых не заканчиваются нулем, но при сложении не образуется дополнительный десяток (25 +34, 48+ 51 и т. п.), и, наконец, суммы, в которых при сложении образуется новый десяток (25+37, 38+56 и т. п.).
Суммы вида 25+5 и 42+28 отнесем соответственно ко второй и третьей группам.
для наглядности рассмотренные виды сумм представлены в табл. 2, где они расположены в порядке возрастания сложности.

Уровни сложности а—ч! определены интуитивно. для того чтобы расположить все 8 случаев сложения в порядке Возрастающей трудности, интуиции недостаточно. В самом деле, опираясь только на интуицию, нельзя определённо сказать, чтоб вычислить проще: 22+5 или 20+35; 9+5 или 22+35. А между тем этот вопрос имеет принципиальное значение: в соответствии с дидактическим принципом «от простого к сложному» приемы вычисления должны изучаться по Возрастающей сложности.
Кроме того, поскольку учащиеся должны научиться складывать числа в пределах 100 в уме, то ясно, что большое количество приемов сложения делало бы эту задачу трудно выполнимой. Поэтому желательно уменьшить число таких приемов, обобщив их.
Исходя из особенностей абака как средства интерпретации, определим вычислительные приемы для случаев (1)—(8).
(1)
Приведем примерный диалог между учителем и учеником при работе с абаком над приемом вычисления этой суммы.
У ч и т ел ь: В кармане наборного полотна 9 квадратов. Можно ли в этот карман положить квадраты, соответствующие второму слагаемому?
У ч е н и к: Нет, В этот карман можно положить только один квадрат.
Уч и т ел в: Сколько квадратов еще останется положить?
Ученик: 4 квадрата.
Учитель: Как ты это определил?
У ч е н и к: 5 — это 4 и 1. Один положить можно к 9, значит, останется положить еще 4.
У ч и т е л ь: Заполни наборное полотно и говори вслух, как ты это делаешь.
У ч е н и к: 1 квадрат поместим к 9 квадратам. Получится 10 квадратов. Заменим их полоской, 4 квадрата поместим в другой карман.
Выполняются соответствующие математические записи: 9+ (1 + +4) — выясняется, сколько квадратов из 5 можно добавить в карман с первым слагаемым и сколько квадратов останется; (9+1)+ +4—заполняется карман с первым слагаемым; 10+4 — квадраты в этом кармане заменяются полоской («десятком)>) и 4 квадрата укладываются в другой карман абака. Сумма 10+4 находится по «определению» чисел второго десятка.
(2)20+5.
При знакомстве с нумерацией двузначных чисел учащиеся учились называть числа, состоящие из нескольких десятков и нескольких единиц: 20+5 это 2 десятка и 5 единиц, т. е. 25.
(3) 22+5.
Учащиеся знают, как показать на абаке первое слагаемое. По правилу работы с абаком 5 квадратов (второе слагаемое) укладывается в кармашек с двумя единицами первого слагаемого. Математически это описывается так: (20+2) +5=20+ (2+5). для разложения числа 22 на разрядные слагаемые используется правило называния двузначных чисел или вычислительный прием (2). Этот прием используется для получения ответа: 20+7=27.
(4)28+5.
Первое слагаемое представляется на абаке двумя полосками и
8 отдельными квадратами. Второе слагаемое — квадратами. Значит,
согласно правилу работы с абаком, второе слагаемое прибавляется
к 8. Таким образом:
(20+8) +5— прием (2);
20-(.5) —прием (1);
20+ 13 прием нахождения значения суммы такого вида еще не рассматривался. Он будет изучаться после приема (6): сложение двузначных слагаемых, одно из которых круглые десятки. Значит, случай сложения (4) должен изучаться после случая (6)
(5) 20+30.
Абак заполняется сначала двумя полосками, а затем в него кладут еще З полоски. Всего в абаке 2+3 полоски, или 5 десятков. Таким образом, прием сложения круглых десятков состоит в подсчете десятков: 2 десятка + З десятка = 5 десятков, т. е. в сложении однозначных именованных чисел.
(6) 20+35.
В соответствии с приемом (2) число 35 можно представить в виде суммы 30+5. К двум пол9скам (первому слагаемому), находящимся в абаке, укладываются еще З полоски второго слагаемого, а затем в отдельный карман еще 5 квадратов второго слагаемого:
20+ (30+5) = (20+30) +5.
Сумма круглых десятков определяется с помощью приема (5); сумма 50+5—прием (2).
(7) 22+35.
Как и в предыдущем случае, второе слагаемое помещается в абак по частям — отдельно десятки и отдельно единицы:
22+(30-I-5) -1-прием (2);
(22+30) +5 прием (6);
52 + 5 = 57 (прием (3).
(8) 25+36.
Аналогично приемам (6) и (7) второе слагаемое в этой сумме укладывается в абак разрядными единицами — десятками и единицами:
25+(ЗОЧ-6) —прием (2);
(25+30) +6 прием (6);
55+6= 61 —прием (4).
Итак, определены приемы сложения чисел в пределах ста и выявлены связи между этими приемами. Схематически эти связи изображены на рис. 18.
Из схемы видно, что основными являются приемы (1), (2), (5). Остальные 5 представляют собой их комбинации. Таким образом, число вычислительных приемов минимизировано. Теперь определим последовательность изучения различных случаев сложения в пределах 100. Эта задача решена лишь отчасти. Из рис. 18 видно, что 8 выделенных случаев сложения упорядочены частично. Так, например, суммы вида 22 +35 (7) нужно рассматривать после изучения приемов вычисления сумм вида 20+5 (2), 22+5 (3), 20+35 (6). Однако схема не содержит информации о том, какой случай сложения следует изучать раньше— (7) или (1)? (7) или (8)? (7) или (4)?
Таким образом, равно возможны различные варианты последовательности их изучения: (1, 2, 5, 3, 6, 7, 4, 8), (2, 3, 5, 6, 7, 1,4, 8), (1, 2, 3, 5, 6, 4, 8, 7), (5, 2, 6, 1, 4, 8, 3, 7) и т. д.

С дидактической (методической) же точки зрения эти варианты не
равнозначны.
Очевидно, что изучение операции сложения (вычитания) не может происходить в отрыве от усвоения учащимися нумерации натуральных чисел. (Вспомним, что знакомство с числа ми первого десятка происходило одновременно с изучением операций сложения и вычитания: каждое новое число появлялось в результате прибавления к предыдущему числу единицы.) Как известно, нумерация двузначных чисел вводится в следующем порядке: усваиваются названия
и запись чисел второго десятка
(от 11 до 19), затем круглые десятки
и, наконец, остальные двузначные
числа. -2Зб--4’i..
При сложении однозначных чисел с переходом через десяток (суммы вида (1)) получаются числа второго десятка. Естественно, что суммы вида 9+2, 4+7 должны рассматриваться параллельно с изучением нумерации чисел от 11 до 19. Таким образом была бы достигнута преемственность в изучении таблицы сложения: числа от О до 10 учащиеся узнают одновременно с табличными случаями сложения в пределах 10; знакомство с числами следующего десятка связано с изучением остальных случаев табличного сложения. Причем при использовании приема (1) интенсивно «работает» таблица сложения в пределах 10.
При изучении нумерации круглых десятков используется понятие «десяток». Слова «двадцать», «тридцать» и другие служат названиями двух десятков, трех десятков и т. д. Поэтому естественно ввести прием сложения круглых десятков, в котором понятие «десяток» выполняет важную функцию: 10+20 заменяется суммой: 1 десяток+2 десятка=3 десятка, откуда 10+20=30.
Знакомство с остальными числами в пределах 100 предполагает использование понятия разрядных слагаемых: 21 — это два десятка и одна единица, или 20 + 1. Таким образом, изучение приема (2) происходит в неразрывной связи с изучением нумерации двузначных чисел с ненулевыми разрядами единиц.
Известно, что при усвоении разрядного состава чисел учащиеся часто путают разряды десятков и единиц. Поэтому методически целесообразно рассматривать случаи сложения вида 25 + 3 (3) и 25 + +30 (6) непосредственно после введения нумерации двузначных чисел в пределах 100. Причем больший эффект достигался бы при одновременном изучении обоих приемов, так как при этом можно противопоставить не только внешний вид сумм 25+3 и 25+30, но и их значения — 28 и
достаточно трудно убедительно обосновать целесообразность той или иной последовательности изучения остальных приемов, поэтому будем полагаться на интуицию: сначала изучается прием (4), затем (7) и, наконец, (8).
Итак, логико-дидактический анализ темы «Сложение в пределах 100» позволил определить методически целесообразный порядок изучения всевозможных случаев сложения чисел из множества (10, 11,
100}:
9 + 5—э.-20 + 30—.20+5-22 + 3—-28 + 6-*22 + 35—25+36.
22 + 30
(1) (5) (2) (3) и (6) (4) (7) (8)
При изучении приемов устного сложения учащиеся знакомятся с ассоциативным законом сложения. В начальной школе этот закон раскрывается с помощью правил прибавления числа к сумме и суммы к числу.
‚ В § 10 рассматривалась методика знакомства учащихся со скобками в числовых выражениях. Поэтому сразу перейдем к раскрытию содержания методики обучения учащихся названным правилам.
Учитель должен убедить учащихся, что для вычисления значений выражений (а + Ь) + с и а + (Ь + с) действия можно производить в любом порядке, т. е. значение выражений не зависит от порядка выполнения действий. Усвоение учащимися этих правил не вызывает трудностей, если их математическое содержание будет раскрываться с опорой на интуитивные представления детей, их житейский опыт. Учитывая это, в начале изучения, например, правила вычисления суммы (а + Ь) + с учащимся предлагают серию задач, имеющих разный сюжет, но одинаковое математическое содержание, например:
«Мальчик нашел два белых гриба, три подосиновика и четыре подберезовика. Сколько всего грибов нашел мальчик?»; «В вазу положили два яблока, пять слив и три груши. Сколько всего фруктов в вазе?»
Работа над этими задачами ведется по следующему плану. Условие первой задачи конкретизируется: «Мальчик сначала нашел два белых гриба...» На наборном полотне появляется соответствующая иллюстрация. «...Затем три подосиновика...» Иллюстрация на наборном полотне дополняется. «...А потом под березой он нашел еще четыре подберезовика». Учитель устанавливает на наборном полотне еще четыре «гриба». «Сколько всего грибов нашел мальчик?» Выполняется запись: (2 + 3) + 4.
Учащиеся могут заполнить индивидуальные наборные полотна, используя вместо «грибов» геометрические фигуры разного цвета.
Затем читается другой вариант этой же задачи: «Мальчик сначала нашел три подосиновика, потом под березой — четыре подберезовика. После этого ему посчастливилось найти еще два белых гриба». В соответствии с текстом задачи заполняется следующий карман наборного полотна (рис. 19). Составляется соответствующая математическая запись: +4) +2.
Аналогичным образом условие задачи перефразируется. в соот
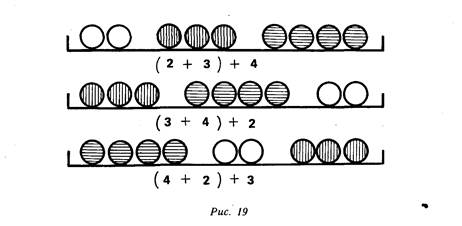
ветствии с выражением (4+2) +3. Заполняется еще один карман наборного полотна (рис. 19).
В заключение делается вывод, что исходную задачу можно решить разными способами (2+3) +4= (3+4) +2. Интуиции детей достаточно для того, чтобы они увидели справедливость данных равенств, не прибегая к вычислениям.
для второй задачи учитель пишет рядом с карманами еще незаполненного наборного полотна по одному выражению: (2 +5) + +3, (2+3) +5, (5+3) +2. Сюжеты к этим выражениям по данной задаче предлагается составить самим учащимся.
Наконец, школьникам можно предложить составить задачу по числовому выражению вида (а + Ь) + с и перефразировать ее условие так, чтобы она решалась с помощью выражений (а + с) + Ь и (Ь+с)+а.
В заключение формулируется правило: прибавить число к сумме можно, складывая числа в любом порядке. Запоминание учащимися более детальной формулировки («чтобы прибавить число к сумме, можно сначала найти значение суммы, а потом прибавить число; можно к первому слагаемому суммы прибавить число, а потом прибавить второе слагаемое суммы...» и т. д.) нецелесообразно. Такие формулировки создают опасность формального усвоения сути правила. Гораздо важнее выработать у учащихся привычку обращаться к задачам, если правило ими забыто.
Правило закрепляется в процессе решения соответствующих числовых примеров. Например: «Запиши удобный способ вычисления значения данных выражений: (8+2) +5; (7+5) +3; (6+5) +5» и т. д. Так как учащиеся еще не изучали прием сложения однозначных чисел с переходом через десяток, последовательность вычислений определяется однозначно.
В ы ч и т а н и е. Выполним логико-дидактический анализ вычитания в пределах 100. Основным наглядным пособием при изучении вычитания также является абак.
Выделим всевозможные виды разностей чисел в пределах 100 (табл. 3).