Оценка точности геодезических сетей нелинейными методами

 

Если координаты пунктов геодезической сети получены путем минимизации целевой функции (3.3), то гиперэллипсоид погрешнос­ти может быть определен в соответствии с теоремой Х.Вольфа [138] по изоповерхности критериальной функции

 

. (4.13)

 

Зная, что для геодезической сети в соответствии с (3.6) для точки минимума

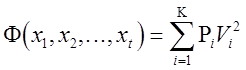, (4.14)

найдем приращение целевой функции из точки минимума до изоповерхности, соответствующей гиперэллипсоиду ошибок, определяя разность (4.13) - (4.14)

. (4.15)

Формула (4.15) лучше равенства (4.13), но задавая прира­щение целевой функции из точки минимума, равное m², невозможно получить средний квадратический гиперэллипсоид ошибок методами нелинейного программирования по заданной изоповерхности.

В связи с этим предлагаем выполнять оценку точности геодезических сетей с использованием нелинейных методов на основе фундаментальной теоремы метода наименьших квадратов, для которой справедливо равенство [33, 40].

 

K_Z = FK_xF^T, (4.16)

 

где F ¾ матрица первых частных производных нелинейной функции по результатам измерений; K_x ¾ корреляционная матрица измерений, С = Р(diag|V|^n-2)

 

F = (A^TCA)^-1A^TC. (4.17)

 

Для обратной матрицы весов вместо (4.16) можно записать

 

Q = FP^-1F^T. (4.18)

 

Если (4.17) подставить в (4.18), то получим известную формулу [22]

 

Q = G^-1 A^TDAG^-1, (4.19)

где G = А^ТСА – информационная матрица Фишера, а D = Р(diag|V|^{2(n – 2)}). Но равенство (4.19) ограничено в применении и используется лишь в методе Lp-оценок. Ее нельзя применять при многокритериальной оптимизации. В последнем случае рекомендуем получать матрицу F численным путем.

Известно, что для матрицы F число строк равно числу параметров, число столбцов ¾ числу измерений. Любой столбец матрицы F можно получить численным методом следующим путем.

1. Получим уравненные координаты всех пунктов геодезической сети , минимизируя целевую функцию (3.1).

2. Изменяем j-ое измерение на малую величину l_j, и вновь выполняем уравнивание сети, получая вектор оценок параметров .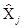

3. Элементы одного столбца S матрицы F при S = 1, …, t можно получить из выражения [4]

 

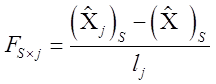. (4.20)

 

Ясно, что для нахождения F необходимо выполнить K уравнительных вычислений.

Если при уравнивании n ¹ 2, т.е. используется отличный от способа наименьших квадратов метод, то в (4.16) вместо K_x подставляется матрица K_n = K_x^n/2. При этом весовая матрицы будет определена из выражения

 

. (4.21)

 

Правильность вычисления матрицы F при любом n проверяется в соответствии с равенством

 

FV = 0, (4.22)

 

где V ¾ вектор поправок в результаты измерений из уравни­вания.

Несмотря на то, что данный способ предлагается применять для геодезических сетей, оценим сначала этим способом прямую и линейную засечки с исходными данными в табл. 4.1.

В табл. 4.5 приведены результаты вычислений для прямой засечки; в табл. 4.6 указаны соответствующие результаты оценки точности.

Таблица 4.5

Матрицы F и векторы V для прямой засечки

 

Показатель степени n	Элементы матрицы F	Вектор V²
	- 0,09583 - 0,00366	0,00061 - 0,00092	- 0,02258 0,04730	0,00 1,85
				0,00
	- 0,07629 - 0,01312	0,03784 - 0,01831	0,00515 0,03439	0,54 0,99
				0,74
	- 0,07233 - 0,01358	0,04470 - 0,01935	0,00977 0,03357	0,66
				0,78
	- 0,07080 - 0,01404	0,04759 - 0,1996	0,01221 0,03357	0,71 0,86
				0,79

 

Таблица 4.6