Вычисление параметров эллипсоида ошибок

 

Если координаты пункта, определенного пространственной геодезической засечкой, найдены путем минимизации целевой функ­ции (3.3), то эллипсоид погрешностей может быть получен в соот­ветствии с теоремой Х.Вольфа [138] по изоповерхности критери­альной функции

 

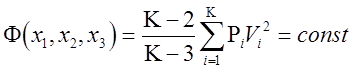. (4.6)

 

Зная, что для многократной пространственной засечки в со­ответствии с (3.6) для точки минимума

 

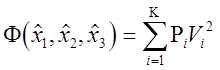, (4.7)

найдем приращение целевой функции из точки минимума до изопо­верхности, соответствующей эллипсоиду ошибок, определяя раз­ность (4.6) - (4.7)

 

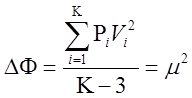. (4.8)

 

Формула (4.8) лучше равенства (4.6), поскольку позволяет выполнять не только апостериорную, но и априорную оценку точ­ности для любых пространственных засечек, включая однократные, при решении которых .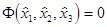

Таким образом, задавая приращение целевой функции из точки минимума, равное m², определим средний квадратический эллипсоид ошибок методами нелинейного программирования по получен­ной изоповерхности.

Прежде чем приступить к изложению методики определения элементов эллипсоида погрешностей по изоповерхности (4.6), сна­чала получим вспомогательные формулы, необходимые для вычисле­ний в системе координат X, Y, Z.

Предположим, что минимизация целевой функции (3.3) завер­шена в точке О (рис.4.3), являющейся центром эллипсоида погрешностей. Из множества изоповерхностей Ф(x, y, z) = const выберем изоповерхность (4.6), близкую к эллипсоиду погрешностей.

Z Zo Z² хо Q х² C P y² M A g w E b O K yo     B D X

Рис. 4.3. Эллипсоид погрешностей и оси координат

 

Перейдем к новой системе x°, y°, z° с началом в точ­ке О и возьмем некоторую произвольную точку P(x°_p, y°_p, z°_p). Направление ОР характеризуется в пространстве косинусами углов w, b, g, которые найдем по координатам точки P по формулам

 

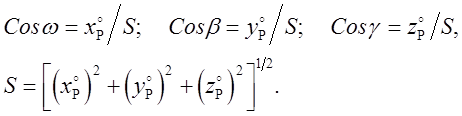(4.9)

 

Плоскость Q, проходящая через точку Р перпен­дикулярно к направлению ОР, пересечет множество изоповерхностей целевой функции. Их след на плоскости Q показан на рис. 4.3 вокруг точки M ¾ минимума целевой функции в плоскости Q. Если плоскость Q будет перпендикулярна к OA, то направление OM совпадет с направлением большой полуоси эллипсоида ошибок. Используя это свойство, можно пост­роить в полученной на рис. 4.3 точке М новую плоскость, перпендикулярную не к ОР, а к ОМ, и, выполнив миними­зацию целевой функции в этой новой плоскости, найти направление, ближайшее к направлению ОА.

Минимизацию целевой функции в секущей плоскости Q удобнее всего осуществлять в системе x², y², z², изменяя лишь переменные x², y². Эта система координат должна быть такой, чтобы возможен был переход к системе x°, y°, z°, и следовательно к системе x, y, z в которой вычисляются зна­чения целевой функции.

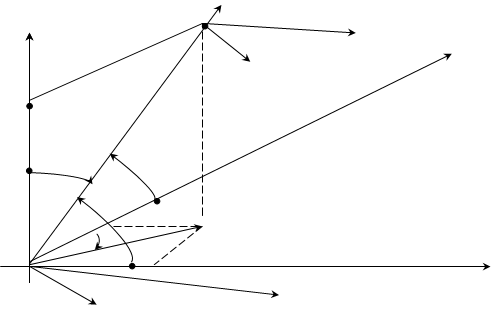
Для вывода соответствующих формул перехода обратимся к рис. 4.4, где изображена система x°, y°, z°, показана точка

Z¢(Z²) P Zo ²x xo y²     H°P     g w   b P¢ a   YO O x¢ y¢1

Рис. 4.4. Системы координат

 

P и обозначены углы w, b, g образованные направле­нием ОР с положительными направлениями осей координат.

Дирекционный угол стороны ОР¢ обозначен a, где Р¢ ¾ проекция точки Р на плоскость х°оу°. Перей­дем к системе x°, y°, z° от вспомогательной системы x¢, y¢, z¢ с началом в точке О, ориентированной следующим об­разом: ось OZ¢ составляет с осью OZ° угол g; ось ОX¢, или направление ОР' образует с осью ox° угол a. Переход от системы x¢, y¢, z¢ к x°, y°, z° осущест­вляется путем преобразований:

1) поворота системы x¢, y¢, z¢ вокруг оси oy¢ против хода часовой стрелки на угол g с помощью матрицы

 

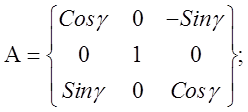
2) поворота полученной системы x*, y*, z° вокруг оси oz° 2 против хода часовой стрелки на угол a с помощью матрицы

 

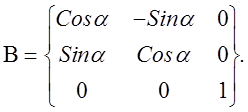
Общий поворот систем координат выражается матричным произ­ведением

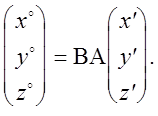
Следовательно,

 

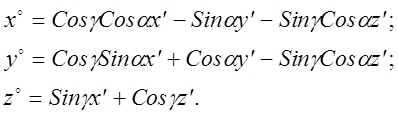
Выполняя параллельный перенос системы x¢, y¢, z¢ по оси Z¢ с началом в точке Р, получим систему x², y², z², а также на основании предыдущих формул ¾ выражение для перехода от x², y², z² к системе x, y, z

 

 

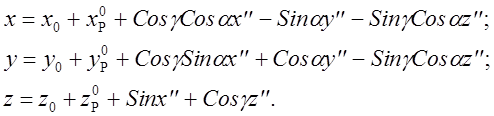
Поскольку в дальнейшем предполагается минимизация целевой функции только в плоскости x²Py² (т.е. в плоскости Q на рис 4.3), то полагая z² = 0, окончательно получим

 

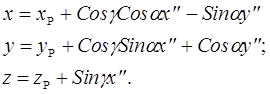(4.10)

Чтобы в процессе минимизации целевой функции в секущей плоскости каждый раз не вычислять коэффициенты при переменных x², y² их необходимо получать заранее по формулам

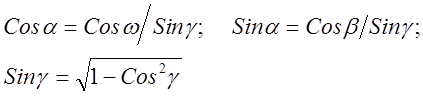(4.11)

где Cosw, Cosb, Cosg ¾ направляющие косинусы отрезка ОР, найденные по (4.9).

Таким образом, зная координаты некоторой точки N(x², y²) на секущей плоскости, используя (4.10), получим координаты N (x, y, z), и вычислим в этой точке значение целевой функции, минимизацию которой в секущей плоскости Q в системе x², y² можно выполнить любыми известными методами нелинейно­го программирования.

Последовательность вычислений при определении элементов эллипсоида погрешностей методом прямого поиска состоит в сле­дующем.

Zo 16 6 7 8 10   2 Yo 5 4     11 12 14 13 15

Х0

1. Найдем с точностью p/4 направление большой полу­оси a. Для этого на полусфере единичного радиуса вычислим значения целевой функции в 17 симметрично расположенных точках (см.рис.4.5), и выделим из них ту, в которой приращение крите­риальной функции будет минимальным. Допустим, это будет точка Р на рис. 4.3.

Рис. 4.5. Вспомогательная полусфера и точки на ней

 

2 Найдем точное направление большой полуоси. Для этого вычислим направляющие косинусы отрезка ОР по формулам (4.9), и найдем минимум целевой функции в секущей плоскости Q, перпендикулярной ОР. Для этого, изменяя координаты x², y² и используя (4.10), осуществим минимизацию целевой функции любым двухмерным алгоритмом нелинейного программиро­вания, например, методом релаксаций. В результате получим ко­ординаты точки М (см. рис.4,3). По направлению ОМ пов­торим вычисления, как и для направления ОР используя новую плоскость Q с минимумом целевой функции в точке М¢. Цель таких приближений ¾ найти точку M^j, лежащую по направлению ОA с тем, чтобы получить направляющие косину­сы большой полуоси с необходимой точностью.

3 Зная направляющие косинусы для ОA, можно вычис­лить координаты любой точки на этом отрезке по формулам

 

 

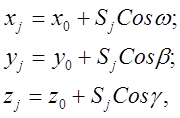
и для поиска значения большой полуоси a, изменяя S_j, выполнить одномерную минимизацию целевой функции

 

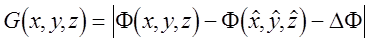, (4.12)

 

где DF ¾ приращения целевой функции из точки минимума до изоповерхности эллипсоида ошибок.

4. Выполняя поиск параметров эллипса в плоскости, прохо­дящей через точку О перпендикулярно к ОА (см.рис.4.3) по методике, изложенной в подразделе 4.1, найдем полуоси b и c и их направляющие косинусы. Здесь также используются формулы (4.10), заменяя в них координаты точки Р на коор­динаты точки O и вычисляя w, b, g, и a по фор­мулам (4.9) и (4Л1) для отрезка ОА.

Как видим, методика поиска элементов эллипсоида погреш­ностей осталась той же, что и для двухмерного случая. Добави­лись лишь новые формулы (4.10).

Решим пример и найдём по предложенной методике элементы эллипсоида погрешностей для пространственной засечки по четы­рем вертикальным углам с исходными данными в табл. 2.16.

Путем минимизации целевой функции (3.3) методом нелиней­ного программирования получены уравненные координаты определяе­мого пункта:

 

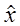= 70,036 м; 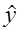= 109,931 м; 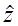= 1,998 м

 

При s_n = 5² определены m = 6,5² и элементы эллип­соида ошибок:

 

a = 0,018 м; Cosa_x = - 0,428; Cosa_y = 0,904; Cosa_z = 0,015;

b = 0,012 м; Cosb_x = - 0,903; Cosb_y = - 0,428; Cosb_z = 0,042;

c = 0,00034 м; Cosc_x = 0,031; Cosc_y = 0,031; Cosc_z = 0,999;

 

Методом линейной алгебры получены:

 

a = 0,020 м; Cosa_x = - 0,468; Cosa_y = 0,883; Cosa_z = 0,018;

b = 0,011 м; Cosb_x = - 0,882; Cosb_y = 0,469; Cosb_z = - 0,041;

c = 0,00035 м; Cosc_x = 0,045; Cosc_y = 0,004; Cosc_z = 0,999.

 

Отметим следующие недостатки новой методики по сравнению с получением элементов эллипсоида ошибок методами линейной алгебры.

1. Программа для ЭВМ занимает в 2,5 раза больше операторов и трудно отлаживается.

2. Программа примерно в 30 раз дольше считает и занимает на оценку точности одного пункта 2 с. времени на IВМ РС/АТ-386.

Преимущества новой методики заключаются в следующем.

1. Стратегия поиска одинакова для эллипса и эллипсоида погрешностей, не зависящая от вида целевой функции. Например, если та же засечка уравнивалась по методу наименьших модулей путем минимизации целевой функции (3.1) при n = 1, то эл­липсоид ошибок при выборе DF, входящего в (4.12) под ус­ловием постоянства большой полуоси a при использовании функции (3.3), будет таким

 

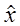= 70,036 м; 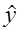= 109,931 м; 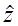= 1,998 м, m = 6,67²;

a = 0,018 м; Cosa_x = - 0,052; Cosa_y = 0,999; Cosa_z = 0;

b = 0,013 м; Cosb_x = 0,997; Cosb_y = 0,052; Cosb_z = - 0,061;

c = 0,00034 м; Cosc_x = 0,061; Cosc_y = 0,003; Cosc_z = 0,998.

 

2. Методика устойчива при любом качестве засечек и не даст деления на ноль даже в вырожденном случае.