Вычисление параметров эллипса ошибок

ГЛАВА 4

ОЦЕНКА ТОЧНОСТИ РЕЗУЛЬТАТОВ УРАВНИВАНИЯ МЕТОДАМИ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

 

Вычисление параметров эллипса ошибок

 

Если координаты пункта, определенного геодезической засечкой, получены путем минимизации целевой функции (3.3), то эллипс погрешностей может быть получен в соответствии с теоре­мой П.Верхмейстера [136] по изолинии критериальной функции

 

. (4.1)

 

Зная, что для многократной засечки в соответствии с (3.6) для точки минимума

, (4.2)

найдем приращение целевой функции из точки минимума до изоли­нии, соответствующей эллипсу ошибок, определяя разность (4.1) - (4.2),

. (4.3)

Формула (4.3) лучше равенства (4.1), поскольку позволяет выполнять не только апостериорную, но и априорную оценку точ­ности для любых засечек, включая однократные, при решении которых .

Таким образом, задавая приращение целевой функций из точки минимума, равное m2, определим средний квадратический эллипс ошибок методами нелинейного программирования по получен­ной изолинии.

Для разъяснения методики вычисления элементов эллипса погрешностей обратимся к рис.4.1, где изображена изолиния (4.1) и точкой О обозначен центр эллипса, совпадающий с минимумом целевой функции. Из точки О проведем оси коор­динат х1¢, х2¢ параллельно осям х1 и х2 для того, чтобы показать не только большую а и малую в полу­оси эллипса, но и угол поворота Q.

 

x¢1   N2   N3 P1 P8 P2 A N1 - Q D a b P1 P3 x2 O C     P6 B P4   P5  

Рис. 4.1. Эллипс ошибок и вспомогательная окружность.

 

Сначала определим прямым поиском ориентировку большой по­луоси эллипса относительно осей координат. Здесь учтем, что большая полуось направлена в сторону наименьшего изменения целевой функции из точки минимума, а малая полуось эллипса ориен­тирована по направлению наискорейшего увеличения солевой функ­ции. Чтобы найти приближенно Q с точностью p/4, по­строим из точки О вспомогательную окружность единичного радиуса и, выбрав на ней восемь симметрично расположенных точек Рi, найдем пару диаметрально расположенных точек, со­ответствующую наименьшему приращению критериальной функции. На рис. 4.1 это будут точки Р4 и Р8. Для уточнения угла Q найдем минимум целевой функции по касательной N1 N2 к окружности в точке Р8, и получим координаты точки N3, по которым вычислим дирекционный угол ОN3 и следователь­но, угол Q.

По направлениям ОA, ОB, ОС и ОD вы­полним одномерную минимизацию целевой функции

 

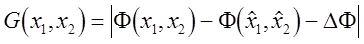. (4.4)

 

и получим координаты точек A, B, C, D следовательно, большую полуось эллипса малую полуось .

По элементам эллипса ошибок можно вычислить элементы об­ратной матрицы по формулам

 

. (4.5)

 

Ошибка положения пункта будет такой .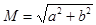

Рассмотрим два примера: прямая и линейная засечки с исход­ными данными, представленными в табл. 4.1.

Таблица 4.1.